5.2. Алгоритм расчетов

Алгоритм расчетов при корреляционном анализе связи пар­ной корреляции состоит из ряда этапов.

Этап 1. Производится отбор наиболее важных сущест­венных факторов, влияющих на результативный показатель. При отборе факторов учитываются причинно-следственные связи между показателями, причем все факторы должны быть количественно измеримы. Большую помощь при отборе фак­торов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. Отбор показателей для анализа и придание им статуса фактора или результативного значения осуществляются на основе знания экономических законов. На­пример, знание закона спроса и предложения помогает изучить влияние ценового фактора на изменение спроса. Отобранные для анализа показатели и результаты наблюдений за их изме­нением помещаются в таблицу, в которой факторные признаки располагаются в порядке возрастания или убывания, т.е. ран­жируются.

Этап 2. Данные из таблицы наносятся на плоскость коор­динат – строится корреляционное поле.

Этап 3. Производится обоснование формы связи:

• по форме корреляционного поля;

• путем визуального анализа ранжированного ряда.

Подобное обоснование является приблизительным и нуж­дается в дальнейшем уточнении с помощью ошибки аппрок­симации.

Форма связи определяет дальнейшие действия корреляцион­ного анализа.

Если связь носит прямолинейный характер, то рассчитывает­ся коэффициент корреляции.

Если связь криволинейная, то прежде всего определяются теоретические значения у_х. С этой целью решается уравнение регрессии, описывающее связь между изучаемыми показателями. Затем рассчитывается корреляционное отношение.

Корреляционное отношение, или коэффициент корреляции, дает количественную оценку тесноты связи, характеризует силу влияния факторных признаков на результативные.

При прямолинейной форме связи коэффициент корреляции рассчитывается по формуле:

Коэффициент корреляции может быть представлен и как сред­нее значение произведений нормированных отклонений (t_x, t_y).

Нормированные отклонения определяются по формулам:

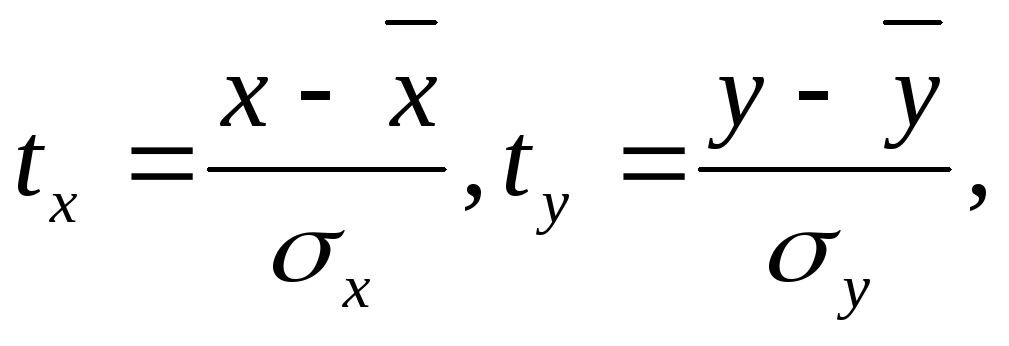
где σ_x, σ_y - средние квадратические отклонения:

Если коэффициент корреляции возвести в квадрат, то полу­чим коэффициент (индекс) детерминации, который показывает, чему равна доля влияния изучаемого фактора на совокупный показатель.

При значениях тесноты связи меньше 0,7 величина индекса детерминации d всегда будет меньше 50%. Это означает, что на долю вариации факторного признака х приходится меньшая до­ля по сравнению с другими признаками, влияющими на изме­нение результативного показателя. Синтезированные при таких условиях математические модели связи практического значения не имеют.

Если значения показателей тесноты связи более 0,7, выбира­ется уравнение регрессии, с помощью которого описывается форма связи между показателями.

Этап 4. Выбор и решение уравнения регрессии. Выбор конкретного уравнения регрессии, адекватно описывающего форму связи, является довольно сложной процедурой. В услови­ях использования ПЭВМ выбор адекватной модели осуществляется перебором решений, наиболее часто применяемых в анали­зе парной корреляции уравнений регрессии. Если форму связи сразу установить сложно, решают уравнения нескольких типов. Выбор адекватной модели производится на основе средней ошибки ап­проксимации ε:

или

где ỹ_х - теоретическое значение, рассчитанное на основе выбранной модели.

у_хi – индивидуальное значение результативного показателя, рассчитанное по уравнению,

- среднее значение результативного показателя, рассчитанное по уравнению,

у_i – фактические индивидуальные значения результативного показателя,

n – количество наблюдений.

Наибольшее значение ошибки аппроксимации свидетельст­вует о том, что оцениваемая модель дает наиболее адекватное описание формы взаимосвязи. Причем ошибка аппроксимации не должна превышать 0,2, или 20%.

Прямолинейное уравнение регрессии показывает равномер­ное нарастание результативного признака с увеличением фак­торного:

у=а+bх,

параметры а и b определяются на основе системы уравнений:

где n – количество наблюдений.

Коэффициент регрессии b показывает, на сколько единиц в среднем изменяется результативный признак у с изменением на одну единицу факторного признака х. Эта всегда именованная величина b на графике показывает угол наклона прямой.

Свободный член а показывает начальную ординату, т.е. рас­стояние от начала координат до пересечения прямой с осью у.

Значения коэффициентов определяются методом наименьших квадратов. Он основан на предположении, что линия, выравни­вающая эмпирические данные, должна проходить так, чтобы сум­ма квадратов отклонений от этой линии была наименьшей, т.е.

∑(y - у_хi)² = min;

∑(y - у_х)² = 0.

Криволинейная форма связи может быть представлена урав­нением гиперболы, параболы, логарифмической функцией и т.д.:

а) уравнение гиперболы

б) параболическая форма связи может описываться парабо­лическим уравнением, например параболой 2-ro порядка:

у=а+ьх+сх²,

в) при логарифмической форме связи

y=a+b Igx,

Пример: Применение корреляционно-регрессионного анализа рассмотрим на примере прямолинейной зависимости меж­ду факторами х и результативным признаком у. Показате­ли условные, так как назначение примера - продемонст­рировать основные процедуры метода. Обозначим х ­качество товара в баллах, у - розничная цена, руб.

Исходные и расчетные данные приведены в табл. 5.2.

Таблица 5.2.

Данные для расчета коэффициента корреляции

и параметров уравнения прямой

№ п/п	х	у	х-		(х-х)^2				tx*ty	х^2	ху	у^2
1	2	12	-10	-6	100	36	- 1,395	-1,261	1,759	4	24	144
2	4	11	-8	-7	64	49	-1,116	- 1,470	1,641	16	44	121
3	6	14	-6	-2	36	16	- 0,837	-0,840	0,703	36	84	196
4	8	16	-4	-2	16	4	- 0,558	- 0,420	0,234	64	128	256
5	10	17	-2	-1	4	1	- 0,279	- 0,210	0,059	100	170	289
6	12	19	0	1	0	1	0	+0,210	0	144	228	361
7	15	20	3	2	9	4	0,418	+0,420	0,176	225	300	400
8	17	21	5	3	25	9	0,697	+0,704	0,491	289	357	441
9	20	23	8	5	64	25	1,116	+1,050	1,308	400	460	529
10	26	27	14	9	196	81	1,953	+ 1,891	3,693	676	702	729
∑	120	180			514	226	0	0	9,836	1954	2497	3466

Расчет коэффициентов корреляции проводится по формуле:

Зависимость между показателями весьма высокая.

Коэффициент корреляции рассчитываем по формуле:

Рассчитанный коэффициент корреляции показывает, что качество товара - основной ценообразующий фактор.

Коэффициент детерминации d = r², d = 0,98² = 0,96 означает, что цена товара на 96,0% зависит от качества, влияние прочих факторов составляет 4,0%.

Положительное значение коэффициента корреляции свидетельствует о наличии прямой связи между показа­телями.

Определим зависимость между ценой и качеством то­вара на основе уравнения прямой:

у =а +bх.

Составим систему нормальных уравнений по данным табл. 5.2:

Умножив все члены первого уравнения на 12 и вычтя из второго уравнения первое, получим: 514b = 337; b=0,656. подставив полученное значение в первое или второе уравнение, получим а = 10,13.

Уравнение прямой примет вид: у = 10,13 + 0,66х. Коэффициент регpeссии b = 0,66 означает, что при изме­нении качества на 1 балл цена товара возрастает на 0,66 руб.

Этот условный пример показывает возможности метода в изучении зависимости между стохастическими показателями.

Математический аппарат регрессионного и корреляционного анализа оказался очень удобным для определения взаимозави­симостей между различными величинами. Но наряду с просто­той у этих видов анализа имеется существенный недостаток ­– исследуется только линейная зависимость между результирую­щим параметром и независимым фактором.

На практике значительно чаще встречаются многомерные за­висимости, т.е. такие, в которых результирующий параметр за­висит от многих факторов, и зависимости нелинейные.

Определение нелинейной корреляционной зависимости. Одним из способов нахождения зависимости является метод замены переменной. Этот метод довольно часто используется при реше­нии различных математических задач. Он заключается в том, что независимый фактор заменяется некоторой функцией этого фактора, которая переводит нелинейную зависимость в разряд линейных.

Например, рассмотрим нелинейную зависимость вида у = х². Это не что иное, как парабола с вершиной в начале коорди­нат. Зависимость явно нелинейная.

Сделаем замену переменной z = х². После подстановки в исходное уравнение получим зависимость вида у = z, которая уже является линейной. Для нее можно использовать весь ма­тематический аппарат регрессионного и корреляционного анализа, т.е. можно находить регрессионное уравнение, ко­эффициенты парной корреляции, ошибки и т. д.

Некоторые виды подстановок приведены в таблице 5.3.

Таблица 5.3.

Различные виды подстановок, с помощью которых осуществляется переход от нелинейных зависимостей к линейным

№	Вид нелинейной зависимости	Подстановка
1	у=1/( а+ b*x)	у=1 / y
2	у=а+ b/x	x= I/x
3	y=x/(a+b*x)	y= x/ y
4	y=1 / (а+ b*ехр(-x))	x=ехр(-x) y=1 / y
5	y= а*ехр(b*x)	Y = log(y)
6	y =	у=y^2
7	y= ехр[а + b*ехр(x)]	x = ехр(x) y = log(y)
8	у= а*x/(b+x)	x= 1 / x, у=1 / y

Вопросы для самоконтроля

1. Какие способы стохастических (корреляционных) взаимосвязей вы знаете?

2. Какие задачи решает корреляционный анализ?

3. Виды корреляций.

4. Приведите общую формулу корреляционного отношения (η).

5. Как определяется коэффициент корреляции (r)?

6. Этапы корреляционного анализа связи парной корреляции.