Uchebnoe_posobie

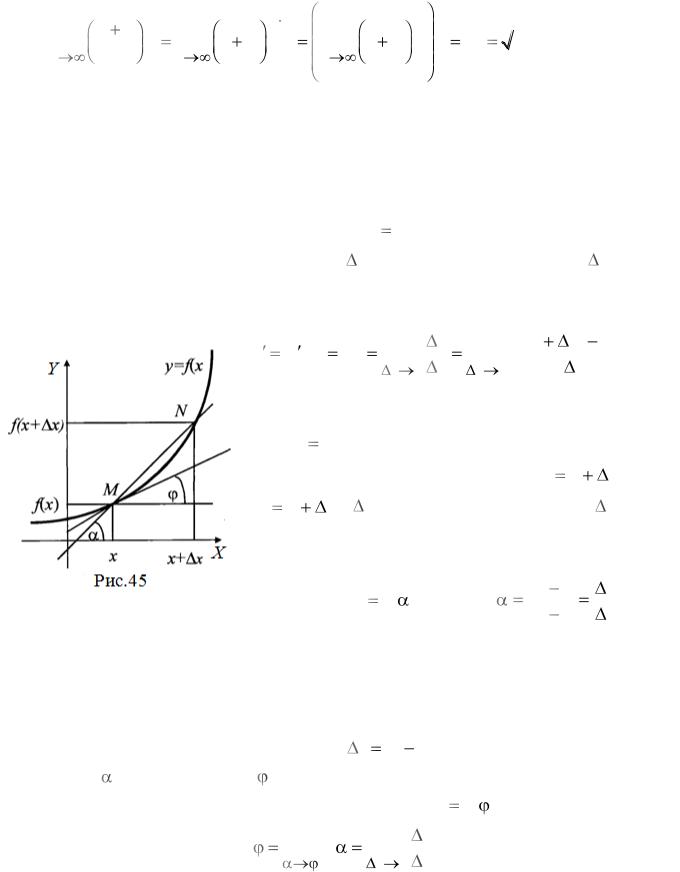
																	1
		1						3 1							3
																	3		1
	3	x x					x		x 3					x		x
lim					lim	1							lim 1						e3			3 e .
		3					3							3
x					x								x

РАЗДЕЛ 4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИ ГЛАВА 1. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦМАЛ ФУНКЦИИ §1. Производная функции. Геометрический и физический смысл производной

Определение. Производной функции

y

f (x) в точке x называется

предел отношения приращения функции

y к приращению аргумента

x ,

рис.45,

при условии, что приращение аргумента стремится к нулю и если

этот

предел

существует:

y

f

(x)

dy

lim

y

lim

f (x x)

f (x)

dx

x

x

x

0

x

0

Пусть

дан

график непрерывной функ-

ции

y f

x .

Возьмем

на

кривой

графика

точки

M x, y

и N x1, y1 ,

где x1

x

x,

y1

y

y ,

x - приращение аргумента,

y -

приращение функции. Проведем секущую

MN ,

угловой коэффициент которой обозна-

чим k1 , т.е. k1

tg

. Тогда: tg

y1

y

y

.

x1

x

x

Предположим, что точка M остается неподвижной,

а точка N , перемещаясь

по кривой, неограниченно приближается к точке M . Тогда:

- секущая MN , поворачивается вокруг точки M ,

приближаясь к поло-

жению касательной;

-

x1 стремится к x , и следовательно,

x

x1 x стремится к нулю;

- угол стремится к углу .

Пусть k угловой коэффициент касательной, т.е. k

tg

. В этом случае:

tg

lim tg

lim

y

x

x

0

Следовательно, угловой коэффициент касательной определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю.

71

k tg	lim	f x	x	f x	y
			x
	x 0

Геометрический смысл производной: производная функции равна тангенсу угла наклона касательной к графику функции в соответствующей точке, т.е. y tg .

Физический смысл производной: производная есть скорость изменения функции в соответствующей точке.

Для одной и той же функции, производная для различных значений аргумента x , может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x . Конкретное значение производной при x a обозначается f (a) или y x a . Операция нахождения производной

от функции f (x) называется дифференцированием этой функции. Для непосредственного нахождения производной, по определению, можно применить следующее практическое правило:

1. Придать x приращение

x и найти новое значение функции, подста-

вив в данную функцию новое значение аргумента x

x .

2. Найти приращение функции

y

f (x

x)

f (x).

3. Составить отношение

y

f (x

x)

f (x)

и найти предел этого

x

x

отношения при

x

0 .

Пример. Найти производную функции y

x2 в произвольной точке и в

точке x

2.

Решение. f (x

x)

(x

x)2;

y

(x

x)2

x2

2x

x

( x)2;

y

lim

2x x

(

x)2

lim (2x

x)

2x;

f (2) 4.

x

x 0

x

0

Пример.

Используя

определение,

найти

производную

функции

y

1

2x в произвольной точке.

Решение.

f (x

x)

1

2(x

x);

y

1

2x

2

x

1 2x;

dy

lim

1 2x 2 x

1 2x

lim

2 x

1

.

dx

x

x( 1 2x 2 x

1 2x)

1 2x

x 0

x 0

Если функция имеет производную в точке

x

x0 , то говорят, что она

дифференцируема в этой точке. Если функция имеет производную в каждой точке данного промежутка, то говорят, что она дифференцируема на

72

этом промежутке. Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y f (x) дифференцируема в некоторой точке x0 , то она в этой точке непрерывна.

Из этой теоремы следует, что в точке разрыва функция не может иметь

производную, так как в этой точке приращение	y равно конечной величине
при x 0 . Обратное утверждение неверно:	существуют непрерывные

функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной). Графические примеры приведены на рис.46:

§2. Правила и формулы дифференцирования

Используя определение производной, можно вывести формулы производных основных элементарных функций и сформулировать правила дифференцирования суммы, разности, произведения и частного функций, а также правило дифференцирования сложной функции.

Основные правила дифференцирования:

Если

обозначить

дифференцируемые

в точке

x

функции, как

f (x) u, g(x) v , то:

1. (u v)

u

v ; 2.

(u v)

u v u v ;

3. (C u)

C u , C Const.

4.

u

u

v

v u

, если v 0.

v

v2

Производные основных элементарных функций:

xn

nxn 1

1

C

0

x

2

x

1

1

ex

ex

(ax )

ax ln a

x

x2

73

ln x

1

loga x

1

sin x cos x

x

x ln a

cos x

sin x

tgx

1

ctgx

1

cos2 x

sin2 x

arcsin x

1

arccos x

1

arctgx

1

1 x2

1

x2

1 x2

arcctgx

1

1

x2

Производная сложной функции:

Пусть y

f (u);u

g(x) , причем область значений функции u входит в

область определения функции y . Тогда: y

f (u)

u .

Производные высших порядков:

Пусть функция

f (x) - дифференцируема на некотором интервале. То-

гда дифференцируя ее, получим первую производную

y f

(x)

df (x)

. Ес-

dx

ли найти производную функции

f (x) ,

то получим вторую производную

функции

f (x) : y

f (x)

d 2 f (x)

, т.е.

y ( y )

или

d 2 y d dy

.

Этот

dx2

dx2

dx

dx

процесс

можно

продолжить

и

далее,

находя

производные

порядка n :

d n y

d

d n 1y

. Все производные, начиная со второй, называются произ-

dxn

dx

dxn 1

водными высших порядков.

§3. Примеры дифференцирования функций

Пример. Продифференцировать функцию y

3x7

2x5

3x2

1.

Решение.

y

3x7

2x5

3x2

1

3x7

2x5

3x2

1 3 x7

2 x5

3 x2

0 3 7x6

2 5x4

3 2x 21x6

10x4

6x; y 21x6

10x4 6x.

Пример. Найти производную функции y

5

x2

x3

x4

3 .

Решение.

y

5 x2 x3

x4

3

x4

3 5 x2

x3

2x 3x2

x4

3

74

4x3 5 x2

x3

2x5

6x 3x6

9x2

20x3

4x5

4x6

7x6

6x5

20x3

9x2

6x.

Пример. Продифференцировать функцию y

x2

3

.

2x

1

Решение.

x2

3 2x 1

2x 1 x2

3 2x 2x 1 2 x2

3

2 x2

x 3

y

.

2x 1 2

2x 1 2

2x 1 2

9

Пример. Найти производную сложной функции y

x3 5x 7 .

Решение.

Составляющими

данной

функции

являются:

y u9,u

x3

5x

7. Согласно правилу дифференцирования сложной функ-

9 x3

8

ции, находим y

x

y

u

x

5x

7

u

x3 5x 7

9 x3

8

5x 7 3x2

5 .

Пример. Найти производную функции y

3

5

3x 2x2 2 .

2

2x2.

Решение.

y

u 3 ,u

5

3x

2

1

2

3 4x

y

5 3x 2x2

3 5 3x 2x2

.

3

3 3

5 3x 2x

2

Пример. Найти вторую производную функции y

x5

2x3

x

3.

Решение.

y

5x4

6x2

1;

y

y

5x4

6x2

1

20x3

12x.

			§4. Дифференциал функции
		Пусть дана функция y		f (x) , дифференцируемая в точке x . Это зна-
	чит,	что функция в точке		x имеет производную, т.е. существует
	lim	y	y . Следовательно,	для функции f (x) выполняется равенство
		x
	x 0

75

	y	y	,	где	0 при	x 0 . Умножив обе части этого равенства на
	x
	x , получим			y	y x	x . Здесь y есть функция от x и не зависит от x ;
следовательно					x входит в первое слагаемое в первой степени, т.е. линейно.

Поэтому первое слагаемое представляет собой линейную часть приращения функции, про второе слагаемое этого сказать нельзя, поскольку также зави-

сит от x .
Тогда при x	0 вторым слагаемым	x можно пренебречь, и первое
слагаемое y x будет являться главной частью приращения функции.
Определение.	Главная часть приращения функции, линейная относи-

тельно приращения аргумента, называется дифференциалом функции и обозначается dy y x.

Таким образом, для всякой функции ее производная зависит только от одной переменной x , тогда как ее дифференциал от двух независимых друг

от друга переменных

x и

x .

Рассмотрим график непрерывной функ-

ции y

f (x) , рис.47.

Производная функции в

точке с абсциссой

x

равна тангенсу угла на-

клона касательной к положительному направ-

лению оси Ox , т.е. y

tg

lim

y

. Из ри-

x 0

x

сунка видно, что касательная разбивает при-

ращение функции

y NM1

на два отрезка:

M1K , соответствующий слагаемому

x , и

NK , соответствующий слагае-

мому y

x .

Если приращение аргумента стремится к нулю (точка M1 стремится за-

нять положение M ),

то отрезок M1K уменьшается значительно

быстрее,

чем отрезок NK . Таким образом, приращение ординаты касательной NK яв-

ляется

главной частью приращения

функции

y

f (x) . Из треугольника

MNK находим MK

MNtg . Так как MN

x,tg

y ,

то

NK

y x dy.

Определение.

Дифференциал

функции

y

f (x) , соответствующей

данным значениям x

и x , равен приращению ординаты касательной к кри-

вой y

f (x) в данной точке x .

76

Рассмотрим функцию y x . Из формулы dy y x получаем dx x , т.е. дифференциал независимой переменной dx совпадает с его приращением

x . Учитывая это, дифференциал функции можно вычислить по формуле

dy	y dx .
Так, если y x3 , то dy (x3) dx	3x2dx ; если y sin x , то dy cos xdx .

Очевидно, чтобы вычислить дифференциал функции, нужно ее производную умножить на дифференциал аргумента. Следовательно, правила нахождения дифференциала остаются теми же, что и для нахождения производных.

Пример. Найти дифференциал функции y

cos

2 x

.

2

Решение.

d cos

2 x

2cos

x

sin

x

1

dx

1

sin xdx

2

2

2

2

2

Пример. Найти дифференциал функции y

a

arctg

x

.

x

a

Решение.

dy

a

arctg

x

dx

a

1

1

dx

a

a

dx.

x

a

x2

1

x

2 a

x2

a2 x2

a

§ 5. Частные производные и полный дифференциал

функции двух переменных

Определение. Величина z

называется функцией двух переменных

x, y , если каждой паре чисел, которые могут быть значениями переменных x, y , соответствует одно или несколько определенных значений величины z , т.е. z f (x, y) . При этом переменные величины x, y называются аргументами функции z .

Определение. Если паре чисел x, y соответствует одно значение z , то функция называется однозначной, а если более одного, то – многозначной.

Определение. Областью определения функции z называется со-

вокупность пар чисел x, y , при которых функция z существует.
Определение. Пусть в некоторой области задана функция	z	f (x, y) .
Возьмем произвольную точку M (x, y) и дадим приращение x	переменной
x , считая при это, что переменная y - постоянная. Тогда		величина

77

x z f (x

x, y)

f (x, y)

называется частным приращением функции по

аргументу x , а предел

lim

x z

lim

f (x

x, y)

f (x, y)

zx

z

f (x, y)

,

x

x

x

x

x

0

x

0

называется частной производной функции z

f (x, y) по аргументу x ,

вычисленный при постоянном

y . Аналогично определяется частная произ-

водная функции по аргументу y :

z

f (x, y)

lim

f (x, y y)

f (x, y)

zy .

y

y

0

y

y

Для частных производных справедливы обычные правила и формулы

дифференцирования.

Пример. Дана функция z

x2

3xy

4y2

x

2y

1. Найти

z

и

z

.

x

y

Решение.

Рассматривая

y

как

постоянную

величину,

получим

z

2x 3y 1

. Рассматривая x

как постоянную, получим

z

3x

8 y

2 .

x

y

Пример . Дана функция z

ex2 y2 . Найти частные производные функ-

ции.

Решение.

z

ex2

y2 (x2

y2 )x 2xex2

y2 ;

z

ex2

y2

(x2

y2 ) y

2 yex2

y2 .

x

y

Определение. Полным

приращением

функции z

f (x, y)

в

точке

M (x, y) называется разность

z

f (x

x, y

y)

f (x, y) ,

где

x

и

y

приращения аргументов.

Определение. Полным дифференциалом функции z

f (x, y)

называ-

ется главная часть полного приращения

z , линейная относительно при-

ращений аргументов

x и

y .

Полный дифференциал функции двух пере-

менных вычисляется по формуле:
dz	z	dx	z	dy fx (x, y)dx f y (x, y)dy	(x, y)	dx		(x, y)	dy .
	x		y		x			y
Пример. Найти полный дифференциал функции z							2x2 y 3xy 1.
Решение.

fx (x, y) 4xy 3y; f y (x, y) 2x2 3x;dz (4xy 3y)dx (2x2 3x)dy.

78

Пример. Найти полный дифференциал функции

z arctg

x

y

.

x

y

Решение.

z

1

2 y

y

,

z

1

2x

x

.

x

1

x y 2

(x y)2

x2

y2

y

1

x y 2

(x y)2

x2 y2

x y

x y

z

z

xdy

ydx

Следовательно, dz

dx

dy

.

x

y

x2

y2

§ 6. Правило Лопиталя

Правило. Если функции f (x) и g (x) дифференцируемы в вблизи точки a , непрерывны в точке a, g (x) отлична от нуля вблизи a и f (a) g(a) 0, то предел отношения функций при x a равен пределу отношения их производных, если этот предел существует, т.е.

	lim	f (x)					lim	f (x)		.
	x a g(x)						x a g (x)
	Пример. Найти предел lim		x2	1			ln x		.
	x 1 ex						e
	Решение. Так как числитель и знаменатель стремятся к нулю при
	x 1 , то имеем неопределенность				0	. Воспользуемся правилом Лопиталя,
				0

т.е. рассмотрим предел отношения производных заданных функций:

2

2x

1

x2

1 ln x

x 1 ln x

2 1 3

lim

lim

lim

x

.

x

x

e

e

x 1

e

e

x 1

ex e

x 1

e

Если отношение производных тоже приводит к неопределенности 00 ,

то правило Лопиталя применяют повторно, пока не раскроется неопределенность или обнаружится, что нужные пределы не существуют.

Пример. Найти предел	lim	ex	e	x 2x	.
			x	sin x
	x 0
Решение.

79

lim

ex e

x 2x 0

lim

ex

e x

2x

lim

ex

e x

2 0

x

sin x

0

(x

sin x)

1

cos x

0

x 0

x

0

x

0

lim

ex

e x

2

lim

ex e x

0

lim

ex

e x

lim

ex e x

2.

sin x

0

(sin x)

cos x

x

0

1

cos x

x

0

x 0

x 0

Данное правило применимо и для раскрытия неопределенности

. В

случае неопределенности вида 0

или

следует алгебраически преоб-

разовать данную функцию так, чтобы привести ее к неопределенности вида

0	или		и далее воспользоваться правилом Лопиталя.
0

Пример. Найти предел lim( x2 ln x) .

x 0

Решение. lim x2 ln x 0	lim	ln x
x 0	x 0 x 2

Пример. Найти предел

lim

1

1

x

ex 1

x 0

Решение.

lim

1

1

x

ex 1

x 0

lim

ex

1

x

0

lim

ex

1

x 0 x ex

1

0

x 0 ex

1 xex

lim	x 1		1	lim x2 0
	2x 3
x 0			2 x 0

.

lim	ex	1		.
x 0 ex 2 x		2

§7. Исследование функций с помощью производной

7.1Интервалы монотонности функции.

Интервалы, на которых функция только возрастает или только убывает,

называются интервалами монотонности.

Теорема. Если производная функции y f (x) положительна (отрицательна) в некотором интервале, то функция в этом интервале монотонно возрастает, рис.48, (монотонно убывает, рис.49).

80