Uchebnoe_posobie

Негосударственное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский институт гостеприимства»

Кафедра математики и информатики

А.Г.Лавров

МАТЕМАТИКА

Учебное пособие

Часть 1

Линейная алгебра. Аналитическая геометрия.

Введение в анализ. Дифференциальное исчисление.

Санкт-Петербург

2013

УДК 51 (075)

ББК 22.1я7

Одобрено и рекомендовано к изданию Учѐным советом Санкт-Петербургского института гостеприимства

Лавров А.Г. Математика. Часть1. Линейная алгебра. Аналитическая геометрия. Введение в анализ. Дифференциальное исчисление: Учеб. пособие. СПб.: СПб институт гостеприимства,2013,98с.

В пособии в достаточно краткой форме изложены основные положения линейной алгебры, аналитической геометрии, введения в анализ и дифференциального исчисления с необходимыми обоснованиями и пояснениями. Основное внимание уделяется практическому освоению изучаемого материала, для чего рассматривается большое число примеров и задач. В конце пособия приведены варианты контрольных работ для самостоятельного решения, экзаменационные вопросы и рекомендуемая литература.

Пособие предназначено для студентов очно-заочной, ускоренной и заочной форм обучения.

УДК 51(075) ББК 22.1я7

© СПИГ, 2013

©Лавров А.Г., 2013

2

РАЗДЕЛ 1. ЛИНЕЙНАЯ АЛГЕБРА ГЛАВА 1. МАТРИЦЫ

§1. Система линейных уравнений

Систему m линейных уравнений с n неизвестными можно записать в

виде:

	a11x1	a12x2	a13x3	.... a1nxn		b1
	a21x1	a22x2	a23x3	....	a2nxn	b2	(1)
	....... .. ..... ... ...... .......... ....... ... ...
	am1x1 am2x2		am3x3	.... amnxn		bm
	где, x1, x2,...., xn - неизвестные величины,				aij (i	1,2,..,m; j 1,2,...,n) - числа,

называемые коэффициентами системы ( первый индекс указывает номер уравнения, а второй – номер неизвестного ), а b1,b2,...,bm - числа, которые называются свободными членами.

Решением системы называется совокупность n чисел x1, x2,...., xn , которые, будучи подставленные вместо неизвестных в уравнения, обращают эти уравнения в тождества.

Решить систему – значит найти все ее решения или доказать, что она решения не имеет.

Система, имеющая решение, называется совместной. Если система имеет только одно решение, то она называется определенной. Система, имеющая более чем одно решение, называется неопределенной. Если сис-

тема не имеет решений, то она называется	несовместной. Система, у кото-
рой все свободные члены равны нулю (b1	b2 ... bn 0) , называется одно-

родной. Однородная система всегда совместна, так как n нулей удовлетворяют любому уравнению такой системы.

Для нахождения решений системы (1) приходиться делать ее эквивалентные преобразования, которые превращают ее в новую систему, удобную для решения. Для осуществления эквивалентных преобразований удобней оперировать не всей системой уравнений, а только коэффициентами при неизвестных, из которых составляется таблица, называемая матрицей системы:

a11	a12	a13	...	a1n
a21	a22	a23	... a2n .
...	...	... ... ...
am1	am2	am3	...	amn
		3

§2. Матрицы. Действия над матрицами Определение: матрицей называется множество чисел, образующих

прямоугольную таблицу, которая содержит m строк и n столбцов:

a11	a12	a13	...	a1n
a21	a22	a23	... a2n .
...	...	... ... ...
am1	am2	am3	...	amn

Для любого элемента aij первый индекс означает номер строки, а вто-

рой – номер столбца, где расположен соответствующий элемент матрицы. Сокращенно прямоугольную матрицу типа m n можно записать в ви-

де: A (aij ), где i 1...m; j 1...n.

Если число строк матрицы не равно числу столбцов, то матрица называется прямоугольной. Если m n , то матрица называется квадратной. Число строк или столбцов квадратной матрицы называется ее порядком. Диагональ квадратной матрицы

a11	a12	a13	...	a1n
a21	a22	a23	... a2n		,
...	...	... ... ...
an1	an2	am3	...	ann

содержащая элементы a11, a22, a33,..., ann - называется главной диагональю матрицы. Диагональ, содержащая элементы a1n,a2 n 1 ,a3 n 2 ,...,an1 - назы-

вается вспомогательной диагональю. Матрица, у которой отличны от нуля только элементы, находящиеся на главной диагонали, называется диагональной. Если у диагональной матрицы элементы a11 a22 ... ann 1, то матрица называется единичной. Матрица, все элементы которой равны нулю, называется нулевой.

В прямоугольной матрицы типа m		n возможен случай, когда m	1.
При этом получается матрица – строка:		A a11 a12 .... a1n . Если n	1
	b11
- получаем матрицу – столбец: B	b21	. Если в матрице типа m n , имею-
	...

bm1

4

			a11	a12	a13	...	a1n
	щий вид	A	a21	a22	a23	...	a2n	переставить строки со столбцами,
			...	...	... ... ...
			am1	am2	am3	...	amn

то получим матрицу n m , которая называется транспонированной мат-

a11	a21	a31	...	am1
рицей Aт a12	a22	a32	...	am2 .
... ... ... ... ...
a1n	a2n	a3n	...	amn

Определение: две матрицы называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы рав-

ны: aij bij .

Пример.

Матрица A

a11

a12

a13

и B

b11

b12

b13

равны,

a21

a22

a23

b21

b22

b23

если a11

b11;a12

b12.....a23

b23 .

Определение: Суммой матриц

A и B называют такую матрицу С ,

элементы которой равны сумме соответствующих элементов матриц A и B .

Пусть A

a11

a12

a13

и B

b11

b12

b13

,

a21

a22

a23

b21

b22

b23

тогда сумма матриц

A

B

C

имеет вид

C

c11

c12

c13

,

где

c21

c22

c23

с11

a11

b11;c12

a12

b12.....c23

a23

b23

Пример. Сложить матрицы A и

B , если A

2

4

; B

1

3

, то

1

3

1

4

2

1

4

3

1

7

C

A B

1

1 3

4

0

1 .

Замечание: на сложение матриц распространяются: 1. Переместительный закон, т.е. A B B A

2. Сочетательный закон, т.е. A B C A	B C
Определение: произведением матрицы A на число k называется та-
кая матрица kA , каждый элемент которой равен	kaij , т.е. умножение мат-

рицы на число сводится к умножению на это число всех элементов матрицы.

5

2

1

4

Пример. Необходимо умножить матрицу

A

0

5

3

на число

2

1

0

6

3

12

k 3 . Решение: 3A

0

15

9 .

6

3

0

Определение: произведением матрицы

A

a11

a12

на матрицу

a21

a22

B=

b11

b12

называется матрица:

b21

b22

C

AB

a11b11

a12b21

a11b12

a12b22

.

a21b11

a22b21

a21b12

a22b22

Для того, чтобы найти элемент c11 первой строки и первого столбца

матрицы C , нужно каждый элемент первой строки матрицы A a11

и a12 ум-

ножить на соответствующий элемент первого столбца матрицы B b11 и b21

и полученные произведения сложить: c11				a11b11	a12b21 и т.д.
Правило: чтобы получить элемент, стоящий на пересечении i - ой
строки и j - ого столбца матрицы-произведения, нужно все элементы i - ой
строки матрицы A умножить на соответствующие элементы j - ого столбца
матрицы B и полученные произведения сложить.
Пример. Найти произведение матриц:
3	1	1		1	1	1
A 2	1	2	и B	2	1	1 .
1	2	3		1	0	1

Решение: c11	a11b11	a12b21	a13b31	3 1	1 2 1 1 6
c12	a11b12	a12b22	a13b32	3 1	1	1	1 0	2
c13	a11b13	a12b23	a13b33	3	1	1 1	1 1	1
c21	a21b11	a22b21	a23b31	2 1 1 2 2 1 6 и т.д.
					6	2	1
в результате, матрица-произведение:				C	6	1	1 .
					8	1	4

Правило умножения распространяется и на прямоугольные матрицы. При этом умножение прямоугольной матрицы A на прямоугольную матрицу

6

B имеет смысл только в том случае, когда число столбцов матрицы A равно числу строк матрицы B . В результате умножения двух прямоугольных матриц A и B получается матрица AB , содержащая столько строк, сколь строк в матрице A и столько столбцов, сколько столбцов в матрице B .

								0	1	2		3	1
								2	1	1
Пример. Найти произведение AB , если A											, B	2	1 .
								3	0	1		1	0
								3	7	1
Используя правило умножения прямоугольных матриц, имеем:
	0 3	1	2	2 1	0 1	1	1	2 0			0	1
AB	2 3	1 2		1 1	2 1	1 1		1 0			9	3	.
	3 3	0 2		1 1	3 1	0 1		1 0			10	3
	3 3	7 2		1 1	3 1	7 1		1 0			24	10

Замечания:

1.Произведение матриц не подчиняется переместительному закону, т.е.

AB BA .

2.Произведение матриц подчиняется: сочетательному и распредели-

тельному законом, т.е. A BC				AB C;		A	B C	AC	BC .
3.Произведение двух ненулевых матриц может оказаться равным нуле-
вой матрице.
Примеры.1. Даны матрицы A						2	1	и B	3	1	. Найти произ-
						1	3		1	1
ведения AB и BA .
Решение: AB	2 3		1	1	2 1	1		1	5	3	,
	1	3	3 1		1	1	3	1	0	4
	3 2		1	1		3	1	1 3		5	0
BA	1 2		1		1 1 ( 1)			1 3		3	4 .
2. Даны матрицы A			1	1	и B	1	1	. Найти произведение AB .
			1	1		1	1
Решение: AB	1 1	1		1	1	1	1 1	0	0 .
	1 1	1		1	1	1	1 1	0	0

7

ГЛАВА 2. ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ §1. Определитель матрицы. Свойства определителей

	Определение: определителем матрицы второго порядка						a11	a12
							a21	a22
	называется число a11a22	a12a21 и обозначается	D	a11	a12
				a21	a22

a11a22 a12a21.

Правило: определитель второго порядка равен разности произведений элементов главной диагонали и вспомогательной диагонали.

Пример. Вычислить определитель второго порядка:									2	5	.
									3	4
Решение: D				5		2 4 5 3	8	15 7.
			2
			3	4
Определение: определителем квадратной матрицы третьего по-
a11	a12	a13
рядка a21	a22	a23		называется число			равное	сумме шести слагаемых,
a31	a32	a33

каждое из которых представляет собой произведение трех элементов мат-

рицы: a11a22a33 a21a32a13 a12a23a31 a13a22a31 a12a21a33 a11a23a32 .

Определители третьего порядка записывается так:

a11 a12 a13

Da21 a22 a23 = a31 a32 a33

a11a22a33 a21a32a13 a12a23a31 a13a22a31 a12a21a33 a11a23a32 .

При вычислении определителей третьего порядка удобно пользоваться правилом треугольников (правилом Сарруса). Это правило проиллюстрировано на двух схемах:

Правило Сарруса: Три положительных члена определителя представляют собой произведения элементов главной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали. Три отрицательных его члена есть про-

8

изведения элементов вспомогательной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны вспомогательной диагонали.

Существует еще одно правило, которое позволяет легко получить порядок расчета определителя третьего порядка. Для этого, исходный определитель необходимо представить в виде:

дописав с право первый и второй столбцы. Произведения сомножителей по направлению стрелок слева на право берутся со своими знаками, а справа на лево – с противоположными, т.е. умноженными на (-1). К сожалению, это простое правило не распространяется на определители более высоких порядков.

		3	2	1
Пример.	Вычислить определитель	2	5	3	. Решение:
		3	4	3

		3	2	1	3	2
D		2	5	3	2	5	3 5 3		2 3 3	1 2 4	1 5 3	3 3 4	2 2 3
		3	4	3	3	4
	45		18	8	15	36		12	8.
		Необходимо						обратить внимание на то,				что определители имеют

только квадратные матрицы.

Определитель квадратной матрицы четвертого порядка содержит 24 слагаемых по 4 сомножителя в каждом. Определитель квадратной матрицы пятого порядка – 120 слагаемых по 5 сомножителей в каждом. Определитель n - го порядка содержит n! слагаемых по n сомножителей в каждом. Поэтому вычислить определитель порядка выше трех, пользуясь только определением, практически невозможно. Для того, чтобы вычислять такие определители их упрощают (понижают порядок) используя их свойства.

Свойства определителей:

1. Определитель не изменится, если его строки поменять местами с со-

ответствующими

столбцами,

(т.е.

транспонировать).

a11

a12

a11a22

a12a21

a11

a21

a11a22

a21a12

a21

a22

a12

a22

9

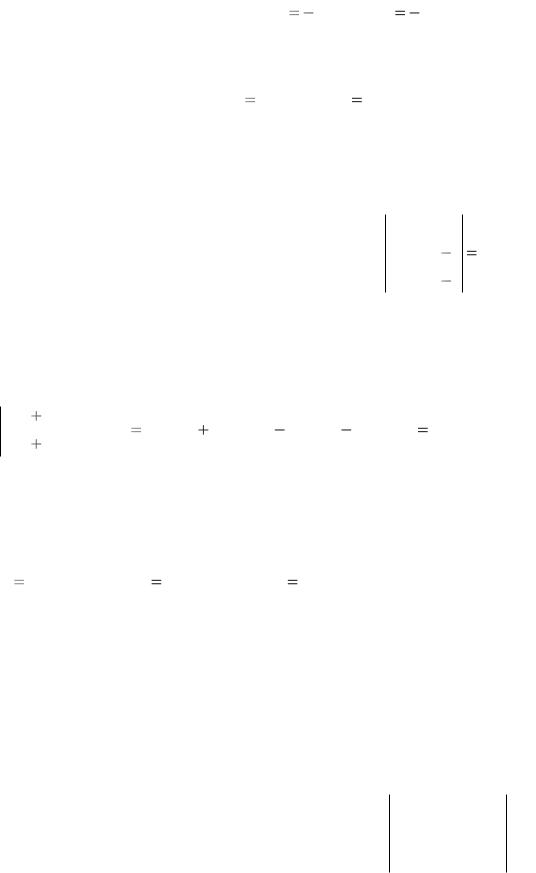
2. При перестановки двух строк или столбцов определитель изменит

свой знак на противоположный:	a11	a12		a21	a22		a12	a11	.
	a21	a22		a11	a12		a22	a21

3. Общий множитель всех элементов строки или столбца можно выне-

сти за знак определителя:	a11	ka12		ka11	ka12	k	a11	a12	.
	a21	ka22		a21	a22		a21	a22

4. Определитель с двумя одинаковыми строками или столбцами равен

нулю.

5. Если все элементы двух строк или столбцов определителя пропор- 3 7 1

циональны, то определитель равен нулю. Например, 2 3 1 0 , т.к. тре- 4 6 2

тья строка получена умножением второй строки на 2.

6. Если к какой-либо строке или столбцу определителя прибавить соответствующие элементы другой строки или столбца, умноженные на одно тоже число, то определитель не изменит своей величины.

a11

ka12

a12

a a

ka

a

a

a

ka

a

a11

a12

.

a21

ka22

a22

11

22

12

22

12

21

12

22

a12

a22

7. Определитель треугольной матрицы, т.е. матрицы у которой все элементы, лежащие выше или ниже главной диагонали, - нули, равен произведению элементов главной диагонали:

	a11	0	0		a11	a12	a13
D	a21	a22	0		0	a22	a23	a11a22a33 .
	a31	a32	a33		0	0	a33

§2. Миноры и алгебраические дополнения элементов определителя Определение: минором Mij элемента aij определителя, называется та-

кой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.

a11 a12 a13

Пусть имеется определитель третьего порядка a21 a22 a23 , тогда,

a31 a32 a33

минор M11 элемента a11, получим вычеркиванием первой строки и первого

10