
- •Лекция № 45. Тема 1 : Числовой ряд. Необходимый признак сходимости
- •1.2. Необходимый признак сходимости. Гармонический ряд
- •Тема 2 : Достаточные признаки сходимости рядов с положительными членами
- •2.1. Признаки сравнения
- •Лекция № 46
- •2.2. Признак Даламбера
- •2.3. Радикальный признак Коши
- •2.4. Интегральный признак Коши
- •Тема 3 : Знакопеременные ряды
- •3.1. Знакочередующиеся ряды. Теорема Лейбница
- •3.2. Абсолютная и условная сходимость
- •Лекция № 47. Тема 4 : Функциональные ряды
- •4.1. Определение функционального ряда
- •4.2. Равномерная сходимость функциональных рядов
- •Тема 5 : Степенные ряды
- •5.1. Определение степенного ряда. Теорема Абеля
- •Лекция № 48
- •5.2. Разложение функций в степенные ряды
- •5.3. Применение рядов Тейлора
- •Лекция № 49. Тема 6 : Ряды Фурье
- •6.1. Определение ряда Фурье
- •6.2. Условия разложения функции в ряд Фурье
- •Лекция № 50
- •6.4. Ряды Фурье для четных и нечетных функций
- •6.5. Разложение непериодических функций в ряд Фурье
- •6.6. Интеграл Фурье
- •Уравнения математической физики Лекция № 51.
- •1. Основные типы уравнений математической физики
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 52. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла (ди)
- •2.2. Вычисление двойного интеграла.
- •Лекция № 53
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Ди в полярной системе координат
- •2.5. Приложения двойного интеграла
- •Лекция № 54
- •Лекция № 55. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 56. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 58.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 58. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 59. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 60
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 61. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 62. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 63.
- •Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 64. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 65. Тема 6 : Основные законы распределения св
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Законы распределения непрерывных случайных величин
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция 66
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •7.1. Неравенство Чебышева
- •7.2. Теорема Чебышева
- •Лекция № 67. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной св
- •Элементы математической статистики Лекция № 68. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 69
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
Лекция № 48
5.2. Разложение функций в степенные ряды
Как было показано
ранее, сумма степенного ряда является
непрерывной и дифференцируемой
функцией в интервале сходимости.
Допустим, что функция
![]() ,
которую будем представлять как сумму
степенного ряда, удовлетворяет этим
условиям в окрестности некоторой точки
,
которую будем представлять как сумму
степенного ряда, удовлетворяет этим
условиям в окрестности некоторой точки![]() .
Тогда её в окрестности этой точки
можно представить в виде ряда
.
Тогда её в окрестности этой точки
можно представить в виде ряда
![]() .
(1)
.
(1)
Требуется найти
коэффициенты
![]() .
Положим в формуле (1)
.
Положим в формуле (1)
![]() ,
получим
,
получим![]() .
Продифференцируем выражение (1)
.
Продифференцируем выражение (1)
![]() .
(2)
.
(2)
Подставим в
выражение (2)
![]() ,
получим
,
получим![]() .
.
Аналогично, дифференцируя п раз:
![]() .
(3)
.
(3)
Подставив значение
![]() в выражение (3), получим
в выражение (3), получим .
.
Тогда, окончательно
 .
(4)
.
(4)
Степенной ряд
(4) называется рядом Тейлора функции
![]() в окрестности точки
в окрестности точки![]() .
Если положить
.
Если положить![]() ,
то получим ряд Маклорена
,
то получим ряд Маклорена
 .
.
Каким условиям должна удовлетворять функция, чтобы её можно было разложить в ряд Тейлора? Воспользуемся формулой Тейлора

где
![]() .
Из этой формулы следует:
Если все производные функции
.
Из этой формулы следует:
Если все производные функции
![]() ограничены в окрестности точки
ограничены в окрестности точки![]() ,
т.е.
,
т.е.![]()
![]() ,
то
,
то
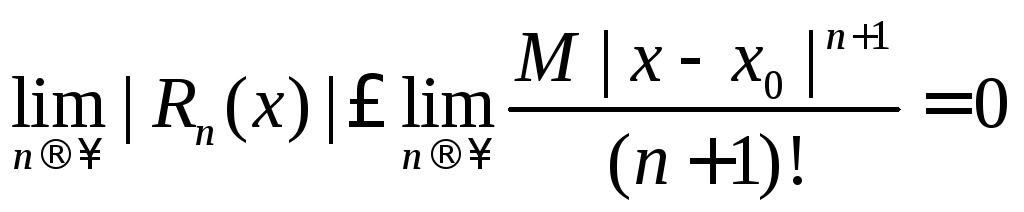
и тогда
![]() ,
т.е. ряд (4) сходится.
,
т.е. ряд (4) сходится.
Рассмотрим
некоторые примеры разложений элементарных
функций в ряд Тейлора при
![]() (ряд Маклорена):
(ряд Маклорена):
![]() Вычислим производные
Вычислим производные
![]() .
Следовательно, получим ряд
.
Следовательно, получим ряд
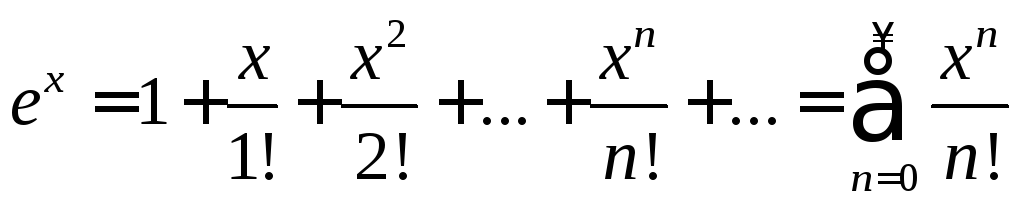 .
(5)
.
(5)
Область сходимости
такого ряда была определена на предыдущей
лекции (прим. 3):
![]() .
.
Аналогично получим





5.3. Применение рядов Тейлора
5.3.1. Приближенное вычисление значений функции.
Рассмотрим
пример. Найти с точностью до 0,01
значение
![]() .
Воспользуемся разложением функции
.
Воспользуемся разложением функции
![]() ,
полагая
,
полагая![]()
 ,
,
так как полученный числовой ряд является знакочередующимся.
5.3.2. Интегрирование с помощью степенных рядов.
Если интегралы не
выражаются через элементарные функции,
то путём разложения подынтегральной
функции в ряд Тейлора и почленного
инте-грирования можно получить выражение
этого интеграла в виде степенного ряда.
Например, рассмотрим функцию
 и представим её в виде степенного
ряда, заменив в ряду (5)
и представим её в виде степенного
ряда, заменив в ряду (5) ,
т.е.
,
т.е.
 .
.
Тогда

 .
.
Таким же методом можно вычислять и определённые интегралы.
Например, вычислим
интеграл Френеля
 с точностью до0,001.
с точностью до0,001.
Воспользуемся
разложением функции
![]() в ряд Тейлора, заменив в нём
в ряд Тейлора, заменив в нём![]() и проинтегрировав,
и проинтегрировав,

 .
.
Так как
 ,
то
,
то .
.
5.3.3. Интегрирование дифференциальных уравнений.
Рассмотрим этот
метод на примере. Найти четыре первых
отличных от нуля членов разложения в
степенной ряд решения дифференциального
уравнения
![]() ,
удовлетворяющего начальному условию
,
удовлетворяющего начальному условию![]() .
.
Решение ищем в виде
 .
.
Тогда
![]()
Вычислим производные:
![]()
![]()
Подставим в ряд
для
![]() полученные значения функции и её
производных
полученные значения функции и её
производных
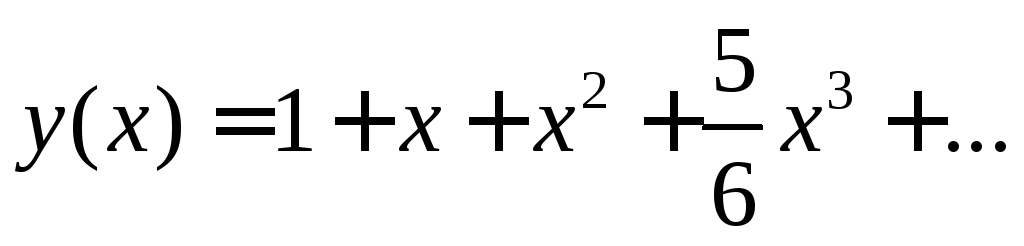 .
.
5.3.4. Докажем
знаменитую формулу Эйлера:
![]() ,
где
,
где![]()
мнимая единица.
мнимая единица.
Воспользуемся разложением в ряд Тейлора функции
![]() .
.
В этом ряду
заменим
![]() .
Тогда получим
.
Тогда получим

С учетом разложений
в ряд функций
![]() и
и![]() получим формулу Эйлера
получим формулу Эйлера
![]() .
.
Лекция № 49. Тема 6 : Ряды Фурье
6.1. Определение ряда Фурье
Определение 1. Функциональный ряд вида
 (1)
(1)
где
![]()
коэффициенты ряда, называется
тригоно-метрическим рядом.
коэффициенты ряда, называется
тригоно-метрическим рядом.
Если ряд (1) сходится,
то его сумма есть периодическая функция
с периодом
![]() .
.
Рассмотрим задачу.
Дана периодическая функция
![]() с периодом
с периодом![]() .
Как и при каких условиях можно найти
тригонометрический ряд, сходящийся к
данной функции?
.
Как и при каких условиях можно найти
тригонометрический ряд, сходящийся к
данной функции?
Пусть
![]() можно представить тригонометрическим
рядом, т.е.
можно представить тригонометрическим
рядом, т.е.
 (2)
(2)
Будем считать, что
ряд (2) сходится равномерно. Тогда его
можно почленно интегрировать в промежутке
![]() .
Определим коэффициенты ряда. Для этого
проинтегрируем его в этом промежутке
.
Определим коэффициенты ряда. Для этого
проинтегрируем его в этом промежутке
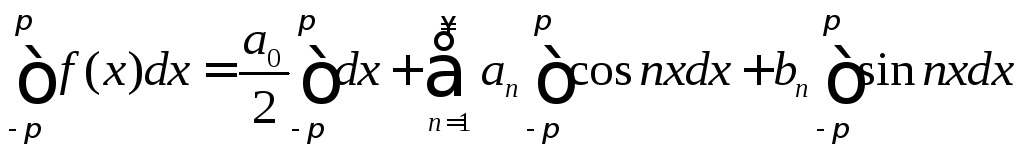 .
(3)
.
(3)
Все интегралы в правой части выражения (3), кроме первого, равны нулю. В силу чего получим
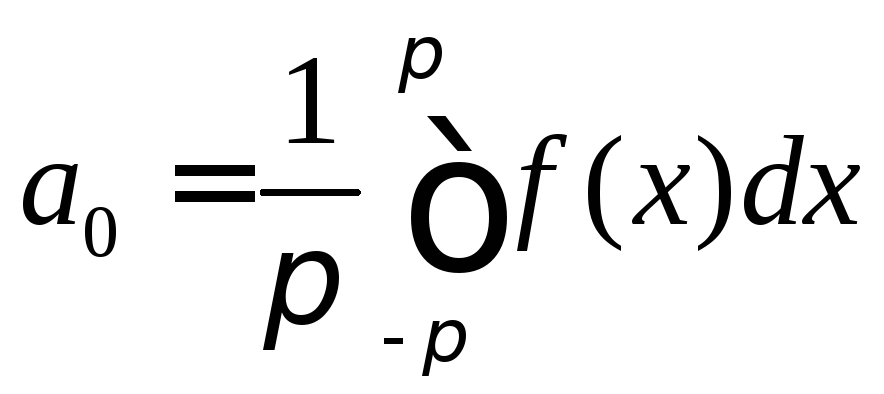 .
(4)
.
(4)
Затем умножим
ряд (2) на
![]() и опять проинтегрируем
и опять проинтегрируем
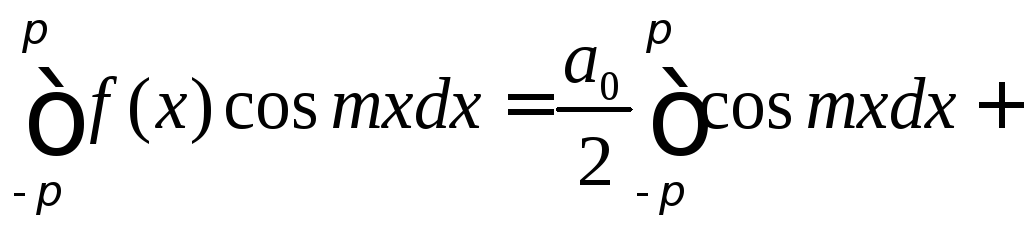
 (5)
(5)
Рассмотрим отдельно в выражении (5) интегралы:

Несложно вычислить

Тогда из выражения (5) следует
 (6)
(6)
Аналогично, умножая
ряд (2) на
![]() и интегрируя, получаем
и интегрируя, получаем
 (7)
(7)
Определение 2. Коэффициенты тригонометрического ряда (2), определяемые по формулам (4), (6), (7), называются коэффициентами ряда Фурье, а сам ряд (2) – рядом Фурье.
Замечание 1.
Интегралы в формулах (4), (6), (7) можно
вычислять по любому отрезку, длина
которого равна
![]() ,
что следует из свойства инте-грала для
периодической функции с периодомТ:
,
что следует из свойства инте-грала для
периодической функции с периодомТ:
 .
.
