2 курс. Ден. ФК, УП, ЕП 12 / Економіко математичні методи та моделі (Оптимізаційні методи) Ч.1 Ден. 2010

	x	=	c	.
b − x
			d
1	1

Задачу для другого інтервалу подамо так:

Z2 =[g(x2 ) + h(b2 − x2 )] → max

за умов

0 ≤ x2 ≤ b2 .

Звідси для будь-якого j -го інтервалу маємо:

Z j =[g(x j ) + h(bj − x j )] → max

за умов

0 ≤ x j ≤ bj .

Загальна задача набирає вигляду:

n

Z = Z1 + Z2 +... + Zn = ∑[g(x j ) + h(bj − x j )] → max

j =1

за умов 0 ≤ x j ≤ bj ( j =1, n) , bj = cx j −1 + d(bj −1 − x j −1) , ( j =1, n) .

Таку задачу розв’язують спеціальними методами.

Методика розв’язування динамічних задач полягає у наступному: динамічний процес розбивається на сукупність послідовних етапів, або кроків. Кожний крок оптимізується окремо, а рішення (розв’язок), згідно з яким система переходить із поточного стану, до нового, вибирається з урахуванням його майбутніх наслідків і не завжди дає найбільший ефект на даному етапі. На останньому кроці приймається рішення (відшукується розв’язок), яке забезпечує максимальний ефект. З огляду на сказане, оптимізація методом динамічного програмування починається з кінця: насамперед планується останній крок. Спираючись на відому інформацію про закінчення передостаннього кроку, на підставі різних гіпотез щодо його закінчення, вибирають управління на останньому кроці. Таке управління називають умовно оптимальним,

70

оскільки знаходять його за припущенням, що попередній крок було здійснено згідно з однією з можливих гіпотез.

Нехай аналізується деякий керований процес, перебіг якого можна розбити на послідовні етапи (кроки), що задаються. Ефективність всього

процесу Z є сумою ефективностей Z j ( j =1, n) окремих кроків:

n

Z = ∑Z j (адитивний критерій)

j =1

або

n

Z = ∏Z j (мультиплікативний критерій).

j=1

Зкожним кроком задачі пов’язане прийняття певного рішення, так

званого крокового управління X j ( j =1, n) , що визначає як ефективність даного етапу, так і всієї операції в цілому.

У задачі динамічного програмування знаходять таке управління

X = (x1, x2 ,..., xn )		всією операцією, яке		максимізує загальну	її
ефективність:
		n
		Z = ∑Z j	→ max .
		j =1
Оптимальним		розв’язком цієї	задачі	є управління X * ,	що
складається із сукупності оптимальних покрокових управлінь
X * = (x*, x*	,..., x* )	і забезпечує	максимальну ефективність		Z *
1 2	n

Z* = max{Z (x)}.

x X

Усі класи задач динамічного програмування розв’язують, керуючись основним принципом: яким би не був стан системи S перед черговим кроком, управління на цьому кроці слід вибрати так, щоб ефективність розглядуваного кроку плюс оптимальна ефективність на всіх наступних кроках була максимальною.

71

Алгоритм розв’язування задач динамічного програмування

1.Специфікуємо стан заданої керованої системи та множину параметрів, що описують цей стан. Стан системи обираємо, маючи на меті забезпечити зв’язок між послідовними етапами перебігу процесу і знайти допустимий розв’язок задачі в цілому як результат оптимізації на кожному кроці окремо. При цьому оптимальні рішення на наступних етапах приймаємо, нехтуючи впливом подальших рішень на прийняті раніше.

2.Розбиваємо динамічний процес (операцію) на кроки, що відповідають, як правило, часовим періодам плануванням або окремим об’єктам (підприємствам, видам продукції, устаткування і т.ін.), стосовно яких розробляються управлінські рішення.

3.	Подаємо перелік	управлінських рішень x j ( j =		)	для	кожного
			1, n
	кроку і відповідні обмеження щодо них.
4.	Визначаємо ефект, що його забезпечує управлінське рішення x j на j -
	го кроці, якщо	перед тим система була у стані S ,			як	функцію
	ефективності:

Z={g(x) + h(b1 − x1)} → max .

5.Досліджуємо, як змінюється стан S системи під впливом

управлінського x j на j -му кроці, переходячи до нового стану:

S'= ϕj (s, x j ) .

6. Будуємо для розглядуваної задачі рекурентну залежність, що визначає умовний оптимальний ефект Z j (s) , починаючи з j -го кроку і до останнього, через вже відому функцію Zi+1(s'):

Z j (s) = max{ f j (s, x j ) + Zi+1(s, x j )}.

72

dn (n =1 N )

Цьому ефекту відповідає умовне оптимальне управління на j -му кроці

(x j (s)). Зауважимо, що аргумент функції Z j +1(s) беремо не s , а

змінений стан системи, тобто s'= ϕj (s, x j ).

7. Здійснюємо умовну оптимізацію останнього n -го кроку, розглядаючи множину станів s , що на один крок віддалені від кінцевого стану, і визначаємо умовний оптимальний ефект на n -му кроці:

Zn (s) = max{ fn}(s, xn ).

Далі знаходимо умовне оптимальне управлінське рішення xn (s),

завдяки якому цей максимум досягається.

8. Виконуємо умовну оптимізацію (n −1)-го, (n − 2) -го і т.д., тобто всіх попередніх кроків за рекурентними залежностями п.6, і для кожного кроку знаходимо оптимальне управління: Z* = Z1(s0 ) .

9.Здійснюємо безумовну оптимізацію управління у “зворотному” напрямі – від початкового стану s0 до кінцевого. Для цього з урахуванням визначеного оптимального управління на першому кроці x1* = x1(s) змінюємо стан системи згідно з п.5. Далі для цього нового стану знаходимо оптимальне управління на другому кроці x2*

і діємо так до останнього кроку.

Завдання для самостійної роботи

1.Фірма повинна розробити календарну програму випуску однорідної продукції на N місяців. Прогноз попиту на продукцію відомий і складає одиниць на місяць. Видатки фірми складаються з витрат на виробництво та плати за зберігання продукції, що очікує на споживання. Місячні витрати на виробництво С(х) є функцією його обсягу. Плата за зберігання складає h на місяць за одиницю продукції. Виробничі потужності забезпечують виготовлення Xmax

73

одиниць продукції на місяць, а складські приміщення витримують зберігання не більше Imax одиниць продукції.

а) N=8
n	1	2	3 4	5 6 7 8
Dn		4 4 4 4 4 4 4 4
			8 +5x, x > 0
С(x) =					, h = 2, X max = 7, Imax = 5 .
			0, x = 0

Питання для самоконтролю

1.В чому полягає загальна постановка задачі динамічного програмування та її геометрична інтерпретація?

2.Сформулюйте принцип оптимальності задачі динамічного програмування?

3.Як знаходяться розв'язки економічних задач методом динамічного програмування?

4.Переличте деякі економічні задачі, які розв’язуються методами динамічного програмування.

Бібліографічний список до теми

[1], [3], [4], [5], [6], [7], [8], [10], [13], [14], [15], [16].

Тема 9. Теорія ігор і прийняття рішень

Мета: опрацювання питань згідно запропонованого плану вивчення теми, вивчення основних понять теорії ігор та методів розв’язання відповідних задач.

План вивчення теми

1.Основні поняття теорії ігор. Приклади ігор. Прийняття рішень в умовах ризику.

2.Ігри з нульовою сумою. Мішані стратегії в матричних іграх.

3.Зведення матричної гри до задачі лінійного програмування.

74

4. Зведення задачі лінійного програмування до матричної гри.

Методичні рекомендації до самостійної роботи

При вивченні цього питання рекомендується ретельне опрацювання теоретичного матеріалу лекції, а саме звернути увагу на

економічну і геометричну інтерпретації задач теорії ігор.

Якщо є кілька конфліктуючих сторін, кожна з яких приймає деяке рішення, обумовлене заданим набором правил, і кожній із сторін є відомим можливий кінцевий стан конфліктної ситуації з заздалегідь визначеними для кожної із сторін платежами, то кажуть, що має місце гра. Задача теорії ігор полягає у виборі такої лінії поведінки даного гравця, відхилення від якої може лише зменшити його виграш. Ситуація називається конфліктною, якщо в ній беруть участь сторони, інтереси яких цілком чи частково протилежні.

Гра — це дійсний чи формальний конфлікт, у якому є принаймні два учасники (гравця), кожний з який прагне досягнення власної мети. Припустимі дії кожного з гравців, спрямовані на досягнення деякої мети,

називаються правилами гри.

Кількісна оцінка результатів гри називається платежем.

Гра називається парною, якщо в ній беруть участь тільки дві сторони.

Свідомий вибір одного з можливих у даній ситуації ходів називають

особистим ходом.

Вибір ходу за допомогою якого-небудь механізму у випадковому добиранню називають випадковим ходом. Щоб гра була математично визнаною, правила гри для кожного випадкового ходу повинні вказувати розподіл ймовірностей можливих наслідків.

Сукупність правил, що однозначно визначають вибір при кожному особистому ході гравця в залежності від сформованої ситуації,

називають стратегією гравця.

75

Парна гра називається грою з нульовою сумою, якщо сума платежів дорівнює нулю, тобто програш одного гравця дорівнює виграшу другого.

Скінченою називають таку гру, в якій у кожного гравця є тільки скінчена кількість стратегій. Кінцеву гру, у якій перший гравець має m стратегій X1, X2 ,..., Xm , а другий гравець — n стратегій Y1,Y2 ,...,Yn ,

називають грою розмірності m×n.

Стратегія гравця називається оптимальною, якщо при багаторазовому повторенні гри вона забезпечує гравцю максимально можливий середній виграш (чи, що теж саме, мінімально можливий

середній програш).

Нехай є два гравці, один із яких може вибрати

i-ту стратегію з m

своїх можливих стратегій

(i =

),

а другий,

не знаючи

вибору

1,

m

першого, вибирає

j-ту стратегію з

n

своїх

можливих стратегій

(j =

). У результаті нехай перший гравець виграє величину

aij, а

1, n

другий програє цю величину.

З чисел aij складемо матрицю

a11

a12 ...

a1n

A =

aij

=

a21

a22 ...

a2n

,

(27)

... ... ... ...

am1

am2 ... amn

Рядки

матриці

А

відповідають

стратегіям першого гравця, а

стовпці — стратегіям другого. Ці стратегії називаються чистими.

Матриця А (30) називається платіжною (чи матрицею гри).

Гру, обумовлену матрицею

А, що має m

рядків і n стовпців,

називають скінченою грою розмірності m× n.

Число

α = maxi (minj

aij )

називається

нижньою ціною

гри чи

максиміном, а відповідна йому стратегія гравця (рядок) – максимінною.

76

Число β = minj (maxi aij ) називається верхньою ціною гри чи

мінімаксом, а відповідна йому стратегія гравця (стовпець) – мінімаксною.

Нижня ціна гри ніколи не перевершує верхньої ціни гри.

Якщо α = β =υ , то число υ називається ціною гри.

Гра, для якої α = β , називається грою з сідловою точкою.

Для гри з сідловою точкою знаходження розв'язку полягає у виборі максимінної і мінімаксної стратегій, що є оптимальними.

Якщо гра, задана матрицею, не має сідлової точки, то для знаходження її розв'язку використовують змішані стратегії.

Вектор, кожна з компонентів якого показує відносну частоту використання гравцем відповідної чистої стратегії, називається

змішаною стратегією даного гравця.

З даного визначення безпосередньо випливає, що сума компонентів зазначеного вектора дорівнює одиниці, а самі компоненти невід'ємні. Зазвичай змішану стратегію першого гравця позначають як вектор U=(u1, u2, …, um), а другого гравця — як вектор Z=(z1, z2,, …,zn),

	ui ≥ 0 ( i =		), z j ≥ 0 (			m	n
де				j =		), ∑ui =1,	∑z j =1.
		1, m			1, n
						i=1	j=1
	Якщо U* — оптимальна стратегія						першого гравця, а Z* —
оптимальна стратегія другого гравця, то число
						n m	*i z*j
					υ = ∑ ∑a ij u
						j=1 i=1

є ціною гри.

Визначення оптимальних стратегій і ціни гри складає процес знаходження розв'язку гри.

Теорема. Усяка матрична гра з нульовою сумою має розв'язок в змішаних стратегіях.

77

Теорема. Для того щоб число υ було ціною гри, а U* і Z* — оптимальними стратегіями, необхідно і достатньо виконання нерівностей

m	(j =		)		n	(i =		).
∑aijui* ≥υ				і	∑aij z*j ≤υ
		1, n					1, m
i=1					j=1

Теорема. Якщо один із гравців застосовує оптимальну змішану стратегію, то його виграш дорівнює ціні гри υ не залежно від того, з якими частотами буде застосовувати другий гравець стратегії, що ввійшли в оптимальну (у тому числі і чисті стратегії).

Розглянемо геометричну інтерпретацію і графічний спосіб розв'язку

найпростіших ігор

2×n та m×2.

Нехай

задано гру платіжною

матрицею

А=

а11

а12 ...

а1n

a

21

a ...

a

2n

22

яку геометрично можна інтерпретувати так. На осі абсцис, відклавши відрізок, який дорівнює умовній 1, приймаємо, що точка Х1(0,0) (лівий кінець встановленого відрізка) зображає стратегію першого гравця X1 , а

точка Х2(1,0) (правий кінець цього ж відрізка) зображує стратегію X2 .

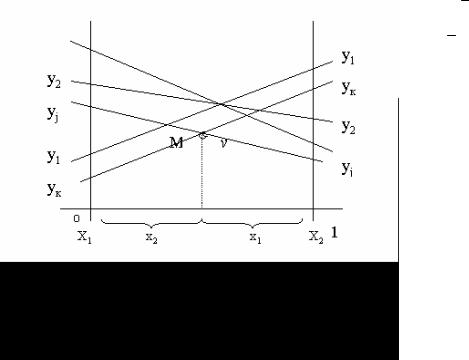
Рис.1.

78

Через точки Х1 і Х2 проводять два перпендикуляри до осі абсцис, на яких відповідно відкладають виграші першого і другого гравців при

послідовному використанні своїх					п можливих стратегій					другим
гравцем.
Стратегії другого гравця			,		, ...,		, ...,		, таким чином,	будуть
		Y1		Y2		Yj		Yn
зображені на графіку прямими	Y1Y1 , Y2Y2 , …, YjYj , …, YnYn ...
Ламана YjMYk на рис. 1	є нижньою границею виграшу. Знаходимо

на ламаній точку М з максимальною ординатою, що дорівнює ціні гри. Абсциса цієї точки позначається через х2. Знаючи, що х1+х2=1, легко знайти оптимальну стратегію першого гравця.

За рисунком 1 виділяють пари «корисних» стратегій другого гравця,

які перетинаються в точці М. Нехай це Yj , Yk .

З огляду на те, що

a1j yj + a1к yk = v ,

yj + yk =1,

знаходять оптимальну змішану стратегію другого гравця.

Аналогічно розв’язується задача розміру mх2. При цьому використовується не нижня границя, як у випадку гри розміру 2хn, а верхня границя, на якій вибирається точка з мінімальною ординатою, що дорівнює ціні гри.

Підсумовуючи сказане, представимо схему графічного методу розв'язку найпростіших матричних ігор:

Будують прямі, що відповідають стратегіям другого гравця (першого гравця).

1.Будують нижню (верхню) границю виграшу.

2.Визначають за рисунком пари «корисних» стратегій з числа побудованих для другого (першого) гравця.

79