2 курс. Ден. ФК, УП, ЕП 12 / Економіко математичні методи та моделі (Оптимізаційні методи) Ч.1 Ден. 2010

3.Вибирають на границі виграшу точку з максимальною (мінімальною) ординатою.

4.Знаходять розв'язок гри.

Зведення задач теорії ігор до задач лінійного програмування. Розглянемо

гру m×n, яка визначається матрицею

(27).

Відповідно до теореми, для оптимальної стратегії першого гравця

U*=(u1*, u2*, …, um*) і ціни гри

υ виконується нерівність

m

(j =

) .

∑aijui* ≥υ

1, n

(28)

i=1

Припустимо для визначеності, що

υ > 0 . Це завжди може бути

досягнуте завдяки тому, що додавання до всіх елементів матриці

А

одного й того ж сталого числа

С не призводить до зміни оптимальних

стратегій, а лише тільки збільшує ціну гри на С.

Поділимо тепер обидві частини нерівності (28) на υ і отримаємо

m

*

∑ aij

ui

≥1

(

j =

) .

1, n

i=1

υ

Поклавши ui* /υ = yi* , маємо

m

∑ aij yi* ≥1 (

j =

) ;

yi* ≥ 0 ( i =

).

1, n

1, m

i=1

m

Використовуючи введене позначення,

перепишемо умову ∑ui* =1

у

i=1

m

вигляді ∑ yi* =1/υ .

i=1

Оскільки перший гравець прагне одержати максимальний виграш, то він повинен забезпечити мінімум значенню 1/υ . З урахуванням цього, визначення оптимальної стратегії першого гравця зводиться до знаходження мінімального значення функції

m

F* = ∑yi

i=1

80

за умов

m	(j =		);	yi ≥ 0 (i =		).
∑aij yi ≥1		1, n			1, m
i=1

Аналогічно показують, що визначення оптимальної стратегії другого гравця зводиться до знаходження максимального значення функції

n

F = ∑xj

j=1

за умов

n	(i =		);	xj ≥ 0 (j =		).
∑aij xj ≤1
		1, m			1, n
j=1

Тут xj=zj/υ. Таким чином, щоб знайти розв'язок даної гри, яка визначена матрицею А, потрібно скласти наступну пару двоїстих задач і знайти їх розв'язок.

n

Пряма задача: знайти максимальне значення функції

F = ∑xj

за

j=1

n

( i =

);

xj ≥ 0 (j =

).

умов ∑aij xj ≤1

1, m

1, n

j=1

m

Двоїста задача: знайти мінімальне значення функції

F* = ∑yi

за

i=1

m

(j =

);

yi ≥ 0 (i =

).

умов ∑aij yi ≥1

1, n

1, m

i−1

Використовуючи розв'язок пари двоїстих задач, одержуємо формули для визначення стратегій і ціни гри:

u* =

y*

=υy* ,

z* =

x*j

=υx* ,

(i =1, m; j =1, n),

i

m

n

i

1

j

j

∑yi*

∑x*j

i=1

j=1

υ =

1

=

1

.

n

m

∑x*j

∑yi*

j=1

i=1

81

Отже, процес знаходження розв'язку гри з використанням методів лінійного програмування включає наступні етапи:

1)Складають пару двоїстих задач лінійного програмування, еквівалентних даній матричній грі.

2)Визначають оптимальні плани пари двоїстих задач.

3)Використовуючи співвідношення між планами пари двоїстих задач, їх оптимальних стратегій і ціною, знаходять розв'язок гри.

Питання для самоконтролю

1.Охарактеризуйте основні поняття теорії ігор. Що називається конфліктною ситуацією?

2.Наведіть приклади ігор.

3.Як здійснюється прийняття рішень в умовах ризику?

4.Що таке гра? Що таке хід гри?

5.Охарактеризуйте ігри з нульовою сумою.

6.Охарактеризуйте мішані стратегії в матричних іграх.

7.Зведення матричної гри до задачі лінійного програмування.

8.Як звести задачу лінійного програмування до матричної гри?

9.Дайте визначення платіжної матриці.

10.Дайте визначення максимінної та мінімаксної стратегії.

11.Яка гра називається скінченою, парною?

12.Які властивості мають оптимальні стратегії гравців? 13.Дайте визначення понять виграш, ціна гри, нижня і верхня

ціни гри.

Бібліографічний список до теми

[1], [3], [4], [5], [6], [7], [8], [10], [13], [14], [15], [16].

82

4. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ПРАКТИЧНИХ ЗАНЯТЬ

МОДУЛЬ І. ОПТИМІЗАЦІЙНІ МЕТОДИ ТА МОДЕЛІ

Змістовий модуль №1. Методи оптимізації на основі задачі лінійного програмування

Практичне заняття №1 Тема 2. Оптимізаційні економіко-математичні моделі

Мета заняття: Набути практичні навички побудови математичних моделей опимізаційних задач – задач лінійного програмування (ЗЛП).

План заняття

1.Економічна та математична постановка оптимізаційних задач. Вибір критерію оптимізації, функціональних та не функціональних обмежень задачі.

2.Розв’язання задач.

Методичні рекомендації до практичного заняття

При виконанні завдань необхідно звернутися до методичних рекомендацій до самостійної роботи з даної теми.

Завдання для практичного заняття

1. На меблевій фабриці зі стандартних листів фанери потрібно вирізати 24, 28, і 18 заготовок трьох розмірів. Лист фанери можна розрізати двома способами. Кількість отриманих заготовок та площу виходів за кожного способу розрізування одного листа фанери наведено в таблиці:

83

	Кількість отриманих заготовок, шт., за
Заготовка		способами
	першим		другим
1	2		6
2	4		4
3	2		3
Площа відходів, см2	18		12

Скільки листів фанери та за яким способом слід розрізати, щоб отримати потрібну кількість заготовок з мінімальними відходами. Побудувати математичну модель задачі.

2. Банк «Золотий долар» збирається видати кредитів на суму, що не перевищує 12 млн. доларів. Типи кредитів і інформація про доходи по них (ставка відсотка) і ризики (ймовірність безнадійних боргів) наведені в таблиці.

	Тип кредиту	Ставка відсотка	Ймовірність
			безнадійних боргів
	Кредити фізичним	0,14	0,1
	особам
	Кредити на купівлю	0,13	0,07
	автомобілів
	Кредити на купівлю	0,12	0,03
	житла
	Сільськогосподарські	0,125	0,05
	кредити
	Комерційні кредити	0,1	0,02

Банк зобов'язаний розмістити не менш 40 % капіталу на потреби сільського господарства й бізнесу (комерційні кредити). Банк також планує вкласти на купівлю житла не менш 50 % від загальної суми кредитів фізичним особам, на купівлю автомобілів. Відношення безнадійних боргів до загальної суми кредитів не повинна перевершувати 0,04. Необхідно побудувати математичну модель задачі, яка максимізує чистий прибуток.

Безнадійні борги вважаються неповерненими, тому вони повинні відніматися з можливого доходу.

3. Фабрика виробляє два види лаку - для внутрішніх і зовнішніх робіт. Для виробництва лаків використовується два вихідних продукти - нафта

84

й кислота. Максимально можливі добові запаси цих продуктів визначаються ємностями для їхнього зберігання та рівні 6 й 8 тонн відповідно. Для виробництва 1 т лаку для внутрішніх робіт витрачається 1 т нафти й 2 т кислоти, а для виробництва 1 т лаку для зовнішніх робіт витрачається 2 т нафти й 1 т кислоти. Добовий попит на лак для зовнішніх робіт не перевищує 2 т. Попит на лак для внутрішніх робіт необмежений. Дохід від реалізації 1 т лаку для внутрішніх робіт дорівнює 3 тис. грн., а дохід від реалізації 1 т лаку для зовнішніх робіт 2 тис. грн. Необхідно визначити, яке кількість лаку кожного виду повинна виробляти фабрика в добу, щоб дохід від його реалізації був максимальним. Скласти математичну модель даної економічної задачі. 4. Розподілити чотирьох робітників за чотирма видами устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані стосовно продуктивності праці кожного робітника на устаткуванні кожного виду наведено в таблиці:

Робітник	Продуктивність праці, грн./год, на устаткуванні
	1	2	3	4
1	12	9	8	7
2	10	7	6	5
3	9	6	4	4
4	8	5	3	2

5. Підприємство електронної промисловості випускає дві моделі радіоприймачів, причому кожна модель виробляється на окремій технологічній лінії. Добовий обсяг першої лінії − 65 виробів, другої лінії

− 45 виробів. На радіоприймач першої моделі витрачається 10 однотипних елементів електронних схем, на радіоприймач другої моделі− 7 таких же елементів. Максимальний добовий запас використовуваних елементів дорівнює 700 одиниць. Прибутки від реалізації одного радіоприймача першої й другої моделей рівні 20 і 12 од. відповідно. Скласти економіко-математично модель задачі.

85

6. Менеджер з цінних паперів має розташувати 100.000$ капіталу. Його вибір обмежений можливими об’єктами інвестування: A, B, C і D. Об’єкт А дозволяє отримувати 6%, В – 8%, С – 10%, а D – 9% річних. Для усіх чотирьох об’єктів ступінь ризику та умови інвестування різні. Щоб не піддавати ризику наявний капітал, менеджер вирішив, що не менше половини інвестицій потрібно вкласти в об’єкти А і В. Щоб забезпечити ліквідність, не менше 25% загальної суми капіталу потрібно вкласти в об’єкт D. Враховуючи можливі зміни у політиці уряду, в об’єкт С слід вкладати не більше 20% інвестицій, тоді як особливості податкової політики потребують, щоб в об’єкт А було вкладено не менше 30% капіталу. Скласти математичну модель задачі визначення оптимального розподілу інвестиції, якщо необхідно отримати максимальний прибуток.

Питання для самоконтролю

1.Економічна та математична постановка оптимізаційних задач. Класифікація оптимізаційних задач.

2.Загальна постановка задачі математичного програмування (МП).

3.Етапи побудови моделі та розв'язання оптимізаційної задачі.

4.Навести приклади економічних задач, які можна звести до задачі ЛП.

5.Загальна постановка задачі лінійного програмування (ЛП). Система гіпотез, що використовуються в задачах ЛП.

6.Сформулювати задачу оптимального використання ресурсів. Що і ній визначає цільова функція? обмеження на змінні?

7.Економічні постановки та математичні моделі деяких задач ЛП. Приклади.

8.Зведення задачі ЛП до канонічного вигляду.

Бібліографічний список до практичного заняття

[1], [3], [4], [5], [6], [7], [8], [10], [13], [14], [15], [16].

86

Практичне заняття №2

Тема 3. Задача лінійного програмування та методи її розв'язування

Мета заняття: Набути практичні навички розв'язання задачі лінійного програмування графічним методом.

План заняття

7.Алгоритм графічного методу розв’язання ЗЛП.

8.Розв’язання задач лінійного програмування графічним методом.

Методичні рекомендації до практичного заняття

При виконанні завдань необхідно звернутися до методичних рекомендацій до самостійної роботи з даної теми.

Завдання для практичного заняття

Навчальні завдання

1. Для виробництва двох видів виробів А и В використовуються три типи технологічного обладнання. Для виробництва одиниці виробу А обладнання першого типу використовується протягом 1 години, обладнання другого типу - 3 години, обладнання третього типу - 3 години. Для виробництва одиниці виробу В обладнання першого типу використовується в протягом 2 годин, обладнання другого типу - 3 годин, обладнання третього типу - 1 години. На виготовлення всіх виробів підприємство може використовувати обладнання першого типу не більш ніж 32 години, обладнання другого типу - 60 годин, обладнання третього типу - 50 годин. Прибуток від реалізації одиниці готового виробу А становить 4 грошові одиниці, а виробу В - 2 грошові одиниці. Скласти план виробництва виробів А и В, що забезпечує максимальний прибуток від їхньої реалізації. Дати геометричне тлумачення завдання, використовуючи для цього її формулювання з обмеженнями - нерівностями.

87

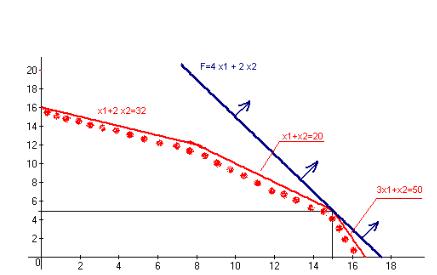
Розв'язання. Перед нами - класична задача лінійного програмування. Під планом виробництва розуміється відповідь на просте питання: скільки виробів А и скільки виробів В треба випустити, щоб прибуток був максимальний.

Запишемо математичну модель задачі:

F(x1, x2 ) = 4x1 + 2x2 → max

x +	2x		≤32
1		2		≤ 60
3x1 + 3x2
3x1 + x2 ≤50
x1 ≥ 0	x2			≥ 0

Розвяжемо задачу графічно. Для цього побудуємо на площині (x1, x2 )

області, які описані обмеженнями-нерівностями, і пряму F = 4x1 + 2x2 ,

що називається цільовою функцією.

Три записаних вище нерівності обмежують на площині багатокутник обмежений ліворуч і знизу координатними осями (тому що шукана кількість виробів позитивно). Графік цільової функції пересувається в напрямку, позначеному стрілкою (по-науковому - у напрямку свого градієнта), доти, поки не досягне граничної точки багатокутника - у нашім випадку це точка - (15 ; 5). У цій точці цільова функція буде досягати максимуму F(15;5) = 60 +10 = 70 .

Рис.2. Графічне розв’язання задачі

88

Завдання для самостійного розвязання

2. Підприємство електронної промисловості випускає дві моделі радіоприймачів, причому кожна модель виробляється на окремій технологічній лінії. Добовий обсяг першої лінії − 65 виробів, другої лінії

−45 виробів. На радіоприймач першої моделі витрачається 10 однотипних елементів електронних схем, на радіоприймач другої моделі

−7 таких же елементів. Максимальний добовий запас використовуваних елементів дорівнює 700 одиниць. Прибутки від реалізації одного радіоприймача першої й другої моделей рівні 20 і 12 од. відповідно. Скласти економіко-математично модель задачі (см. практичне заняття №1). Визначте оптимальні добові обсяги виробництва першої й другої моделей на основі графічного розв'язання завдання.

3. Розв’яжіть графічним методом наступні задачі:

2.1. z = 3x1 + 4x2 (extr),

3x		+ 4x		≥12,
	1		2	≥12,
4x1 +3x2
	0	≤ x	≤ 5,
		1
		x2 ≥ 5.

2.3. z = -2x1 + 3x2 (extr),x1 + 2x2 ≥11,

4x1 + 2x2 ≤15,

x1 +3x2 ≤ 20,0 ≤ x1 ≤ 5,

x ≥ 0.2

2.5. z = -2x1 + 3x2 + 1 (extr),

2x1 + x2 ≥ 3,x1 − 2x2 ≥ 0,x1 ≥1, x2 ≥ 0.

2.2. z = x1 + 4x2 + 2 (extr),

x1 + x2 ≤ 5,4x1 + x2 ≥ 8,x1 − x2 ≤ 0,

x1, x2 ≥ 0.

2.4. z = 2x1 – 25 (extr),

x		+3x				≤15,
	1		2
5x1 + x2 ≤15,
	x1 + x2					≥ 0,
x		−5x		2		≥ 0,
	1
	x1, x2				≥ 0.

2.6. z = 5x1 - x2 (extr),

5x −3x				≤ 32,
	1		2
	x1 − x2 = 0,
	x , x	2	≥ 0.
	1

89