Алгоритмы C++

mulmod (b1, b1, n); if (++b1 == n)

b1 = 0;

g = gcd (abs (b1 - b0), n);

for (unsigned count=0; count<iterations_count && (g == 1 || g == n); count++)

{

mulmod (b0, b0, n); if (++b0 == n)

b0 = 0; mulmod (b1, b1, n); ++b1;

mulmod (b1, b1, n); if (++b1 == n)

b1 = 0;

g = gcd (abs (b1 - b0), n);

}

return g;

}

Метод Бента (модификация метода Полларда "Ро")

Вероятностный тест, быстро даёт ответ далеко не для всех чисел. Возвращает либо найденный делитель, либо 1, если делитель не был найден.

template <class T>

T pollard_bent (T n, unsigned iterations_count = 19)

{

T

b0 = rand() % n,

b1 = (b0*b0 + 2) % n, a = b1;

for (unsigned iteration=0, series_len=1; iteration<iterations_count; iteration++, series_len*=2)

{

T g = gcd (b1-b0, n);

for (unsigned len=0; len<series_len && (g==1 && g==n); len++)

{

b1 = (b1*b1 + 2) % n;

g = gcd (abs(b1-b0), n);

}

b0 = a; a = b1;

if (g != 1 && g != n) return g;

}

return 1;

}

Метод Полларда Монте-Карло

Вероятностный тест, быстро даёт ответ далеко не для всех чисел. Возвращает либо найденный делитель, либо 1, если делитель не был найден.

template <class T>

T pollard_monte_carlo (T n, unsigned m = 100)

{

T b = rand() % (m-2) + 2;

static std::vector<T> primes; static T m_max;

if (primes.empty()) primes.push_back (3);

if (m_max < m)

{

m_max = m;

for (T prime=5; prime<=m; ++++prime)

{

bool is_prime = true;

for (std::vector<T>::const_iterator iter=primes. begin(), end=primes.end();

iter!=end; ++iter)

{

T div = *iter;

if (div*div > prime) break;

if (prime % div == 0)

{

is_prime = false; break;

}

}

if (is_prime)

primes.push_back (prime);

}

}

T g = 1;

for (size_t i=0; i<primes.size() && g==1; i++)

{

T cur = primes[i]; while (cur <= n)

cur *= primes[i]; cur /= primes[i];

b = powmod (b, cur, n); g = gcd (abs(b-1), n); if (g == n)

g = 1;

}

return g;

}

Метод Ферма

Это стопроцентный метод, но он может работать очень медленно, если у числа есть маленькие делители. Поэтому запускать его стоит только после всех остальных методов.

template <class T, class T2>

T ferma (const T & n, T2 unused)

{

T2

x = sq_root (n), y = 0,

r = x*x - y*y - n;

for (;;)

if (r == 0)

return x!=y ? x-y : x+y;

else

if (r > 0)

{

r -= y+y+1; ++y;

}

else

{

r += x+x+1; ++x;

}

}

Тривиальное деление

Этот элементарный метод пригодится, чтобы сразу обрабатывать числа с очень маленькими делителями.

template <class T, class T2>

T2 prime_div_trivial (const T & n, T2 m)

{

//сначала проверяем тривиальные случаи if (n == 2 || n == 3)

return 1; if (n < 2)

return 0; if (even (n))

return 2;

//генерируем простые от 3 до m

T2 pi;

const vector<T2> & primes = get_primes (m, pi);

// делим на все простые

for (std::vector<T2>::const_iterator iter=primes.begin(), end=primes.

end();

iter!=end; ++iter)

{

const T2 & div = *iter; if (div * div > n)

break;

else

if (n % div == 0) return div;

}

if (n < m*m) return 1;

return 0;

}

Собираем всё вместе

Объединяем все методы в одной функции.

Также функция использует тест на простоту, иначе алгоритмы факторизации могут работать очень долго. Например, можно выбрать тест BPSW (читать статью по BPSW).

template <class T, class T2>

void factorize (const T & n, std::map<T,unsigned> & result, T2 unused)

{

if (n == 1)

;

else

// проверяем, не простое ли число if (isprime (n))

++result[n];

else

// если число достаточно маленькое, то его разлагаем простым перебором

if (n < 1000*1000)

{

T div = prime_div_trivial (n, 1000); ++result[div];

factorize (n / div, result, unused);

}

else

{

// число большое, запускаем на нем

алгоритмы факторизации

T div;

//сначала идут быстрые алгоритмы Полларда div = pollard_monte_carlo (n);

if (div == 1)

div = pollard_rho (n); if (div == 1)

div = pollard_p_1 (n); if (div == 1)

div = pollard_bent (n);

//придётся запускать 100%-ый алгоритм Ферма if (div == 1)

div = ferma (n, unused);

//рекурсивно обрабатываем найденные множители factorize (div, result, unused);

factorize (n / div, result, unused);

}

}

Приложение

Скачать [5 КБ] исходник программы, которая использует все указанные методы факторизации и тест BPSW на простоту.

Быстрое преобразование Фурье за O (N log N). Применение к умножению двух полиномов или длинных чисел

Здесь мы рассмотрим алгоритм, который позволяет перемножить два полинома длиной за время		,
что значительно лучше времени	, достигаемого тривиальным алгоритмом умножения. Очевидно, что

умножение двух длинных чисел можно свести к умножению полиномов, поэтому два длинных числа также можно перемножить за время .

Изобретение Быстрого преобразования Фурье приписывается Кули (Coolet) и Таки (Tukey) — 1965 г. На самом деле БПФ неоднократно изобреталось до этого, но важность его в полной мере не осознавалась до появления

современных компьютеров. Некоторые исследователи приписывают открытие БПФ Рунге (Runge) и Кёнигу (Konig) в 1924 г. Наконец, открытие этого метода приписывается ещё Гауссу (Gauss) в 1805 г.

Дискретное преобразование Фурье (ДПФ)

Пусть имеется многочлен -ой степени:

Не теряя общности, можно считать, что является степенью 2. Если в действительности не является степенью 2, то мы просто добавим недостающие коэффициенты, положив их равными нулю.

Из теории функций комплексного переменного известно, что комплексных корней -ой степени из единицы

существует ровно . Обозначим эти корни через	, тогда известно, что	.
Кроме того, один из этих корней	(называемый главным значением корня	-ой степени из

единицы) таков, что все остальные корни являются его степенями: .

Тогда дискретным преобразованием Фурье (ДПФ) (discrete Fourier transform, DFT) многочлена

(или, что то же самое, ДПФ вектора его коэффициентов		) называются значения этого многочлена
в точках	, т.е. это вектор:

Аналогично определяется и обратное дискретное преобразование Фурье (InverseDFT). Обратное ДПФ

для вектора значений многочлена — это вектор коэффициентов многочлена :

Таким образом, если прямое ДПФ переходит от коэффициентов многочлена к его значениям в комплексных корнях 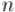- ой степени из единицы, то обратное ДПФ — наоборот, по значениям многочлена восстанавливает коэффициенты многочлена.

Применение ДПФ для быстрого умножения полиномов

Пусть даны два многочлена	и . Посчитаем ДПФ для каждого из них:	и	— это два
вектора-значения многочленов.

Теперь, что происходит при умножении многочленов? Очевидно, в каждой точке их значения просто перемножаются, т.е.

Но это означает, что если мы перемножим вектора	и	, просто умножив каждый элемент

одного вектора на соответствующий ему элемент другого вектора, то мы получим не что иное, как ДПФ от многочлена :

Наконец, применяя обратное ДПФ, получаем:

где, повторимся, справа под произведением двух ДПФ понимается попарные произведения элементов векторов.

Такое произведение, очевидно, требует для вычисления только	операций. Таким образом, если мы
научимся вычислять ДПФ и обратное ДПФ за время	, то и произведение двух полиномов (а, следовательно,
и двух длинных чисел) мы сможем найти за ту же асимптотику.

Следует заметить, что, во-первых, два многочлена следует привести к одной степени (просто дополнив коэффициенты одного из них нулями). Во-вторых, в результате произведения двух многочленов степени получается многочлен степени , поэтому, чтобы результат получился корректным, предварительно нужно

удвоить степени каждого многочлена (опять же, дополнив их нулевыми коэффициентами).

Быстрое преобразование Фурье

Быстрое преобразование Фурье (fast Fourier transform) — это метод, позволяющий вычислять ДПФ за время . Этот метод основывается на свойствах комплексных корней из единицы (а именно, на том, что степени одних корней дают другие корни).

Основная идея БПФ заключается в разделении вектора коэффициентов на два вектора, рекурсивном вычислении ДПФ для них, и объединении результатов в одно БПФ.

Итак, пусть имеется многочлен степени , где — степень двойки, и :

Разделим его на два многочлена, один — с чётными, а другой — с нечётными коэффициентами:

Нетрудно убедиться, что:

Многочлены	и	имеют вдвое меньшую степень, чем многочлен . Если мы сможем за линейное время
по вычисленным		и	вычислить	, то мы и получим искомый алгоритм
быстрого преобразования Фурье (т.к. это стандартная схема алгоритма "разделяй и властвуй", и для неё
известна асимптотическая оценка			).
Итак, пусть мы имеем вычисленные вектора				и	.
Найдём выражения для			.

Во-первых, вспоминая (1), мы сразу получаем значения для первой половины коэффициентов:

Для второй половины коэффициентов после преобразований также получаем простую формулу:

(Здесь мы воспользовались (1), а также тождествами , .)

Итак, в результате мы получили формулы для вычисления всего вектора :

(эти формулы, т.е. две формулы вида	и	, иногда называют "преобразование
бабочки" ("butterfly operation"))

Тем самым, мы окончательно построили алгоритм БПФ.

Обратное БПФ

Итак, пусть дан вектор	— значения многочлена	степени в точках	.
Требуется восстановить коэффициенты	многочлена. Эта известная задача

называется интерполяцией, для этой задачи есть и общие алгоритмы решения, однако в данном случае будет получен очень простой алгоритм (простой тем, что он практически не отличается от прямого БПФ).

ДПФ мы можем записать, согласно его определению, в матричном виде:

Тогда вектор	можно найти, умножив вектор	на обратную матрицу к

матрице, стоящей слева (которая, кстати, называется матрицей Вандермонда):