Алгоритмы C++

Функция Эйлера

Определение

Функция Эйлера 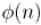или 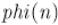— это количество чисел от 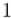до 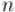, взаимно простых с 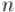. Например, , , , , .

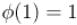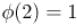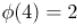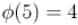Свойства

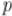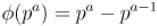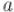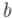Если — простое, то . Кроме того, . Если и взаимно простые, то .

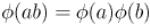Отсюда можно получить функцию Эйлера для любого через его факторизацию (разложение на простые множители):

Реализация

Простейший код, вычисляющий функцию Эйлера, факторизуя число простейшим методом (за ):

int phi (int n) { int result = n;

for (int i=2; i*i<=n; ++i) if (n % i == 0) {

while (n % i == 0) n /= i;

result -= result / i;

}

if (n > 1)

result -= result / n; return result;

}

Ключевое место — это нахождение факторизации числа 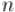, что можно осуществить за время, значительно меньшее 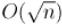: см. Эффективные алгоритмы факторизации.

Приложения функции Эйлера

Самое известное и важное свойство функции Эйлера выражается в теореме Эйлера:

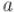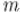где и взаимно просты.

В частном случае, когда 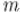простое, теорема Эйлера превращается в так называемую малую теорему Ферма:

Теорема Эйлера достаточно часто встречается в практических приложениях, например, см. Обратный элемент в поле по модулю.

Бинарное возведение в степень

Бинарное (двоичное) возведение в степень — это приём, позволяющий возводить любое число в 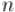-ую степень за умножений (вместо 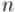умножений при обычном подходе).

Более того, описываемый здесь приём применим к любой ассоциативной операции, а не только к умножению чисел. Напомним, операция называется ассоциативной, если для любых выполняется:

Наиболее очевидное обобщение — на остатки по некоторому модулю (очевидно, ассоциативность сохраняется). Следующим по "популярности" является обобщение на произведение матриц (его ассоциативность общеизвестна).

Алгоритм

Заметим, что для любого числа 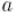и чётного числа 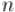выполнимо очевидное тождество (следующее из ассоциативности операции умножения):

Оно и является основным в методе бинарного возведения в степень. Действительно, для чётного 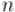мы показали, как, потратив всего одну операцию умножения, можно свести задачу к вдвое меньшей степени.

Осталось понять, что делать, если степень 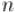нечётна. Здесь мы поступаем очень просто: перейдём к степени 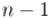, которая будет уже чётной:

Итак, мы фактически нашли рекуррентную формулу: от степени мы переходим, если она чётна, к				, а иначе —
к	. Понятно, что всего будет не более	переходов, прежде чем мы придём к	(базе
рекуррентной формулы). Таким образом, мы получили алгоритм, работающий за			умножений.

Реализация

Простейшая рекурсивная реализация:

int binpow (int a, int n) { if (n == 0)

return 1; if (n % 2 == 1)

return binpow (a, n-1) * a; else {

int b = binpow (a, n/2); return b * b;

}

}

Нерекурсивная реализация, оптимизированная (деления на 2 заменены битовыми операциями):

int binpow (int a, int n) { int res = 1;

while (n)

if (n & 1) { res *= a; --n;

}

else {

a *= a; n >>= 1;

}

return res;

}

Эту реализацию можно ещё несколько упростить, заметив, что возведение 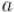в квадрат осуществляется всегда, независимо от того, сработало условие нечётности 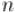или нет:

int binpow (int a, int n) { int res = 1;

while (n) { if (n & 1)

res *= a; a *= a;

n >>= 1;

}

return res;

}

Наконец, стоит отметить, что бинарное возведение в степень уже реализовано в языке Java, но только для класса длинной арифметики BigInteger (функция pow этого класса работает именно по алгоритму бинарного возведения).

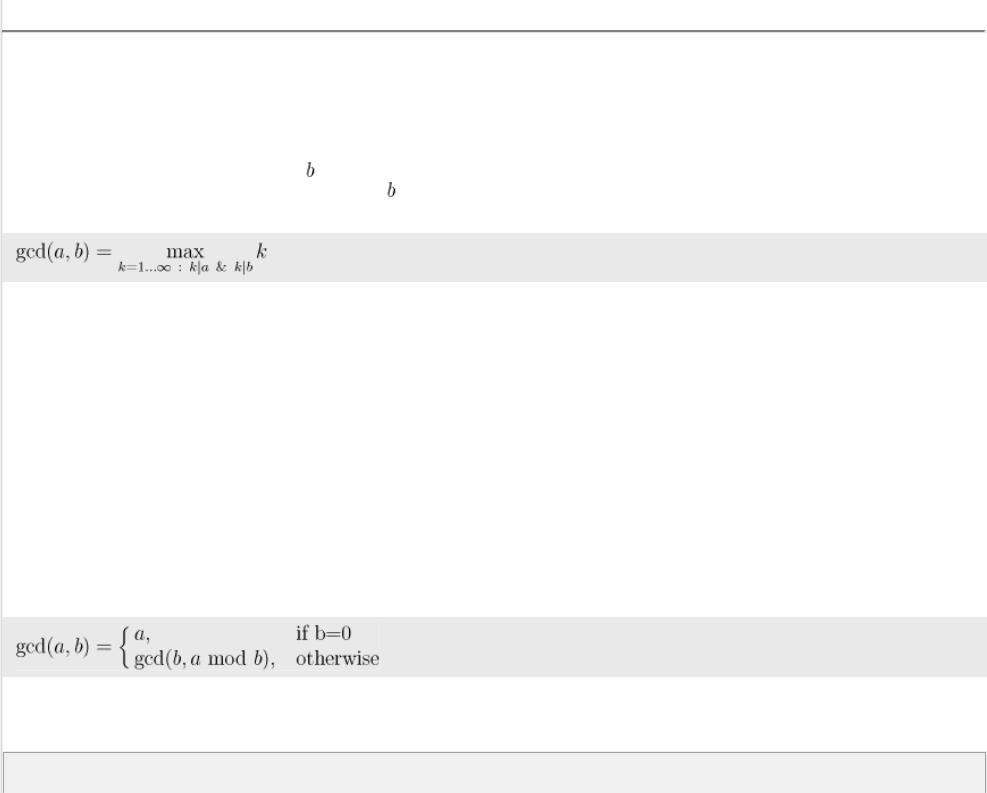
Алгоритм Евклида нахождения НОД (наибольшего общего делителя)

Даны два целых неотрицательных числа 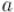и . Требуется найти их наибольший общий делитель, т.е. наибольшее число, которое является делителем одновременно и 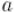, и . На английском языке "наибольший общий делитель" пишется "greatest common divisor", и распространённым его обозначением является :

(здесь символом "" обозначена делимость, т.е. "" обозначае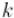т " делит ")

Когда оно из чисел равно нулю, а другое отлично от нуля, их наибольшим общим делителем, согласно определению, будет это второе число. Когда оба числа равны нулю, результат не определён (подойдёт любое бесконечно большое число), мы положим в этом случае наибольший общий делитель равным нулю. Поэтому можно говорить о таком правиле: если одно из чисел равно нулю, то их наибольший общий делитель равен второму числу.

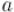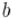Алгоритм Евклида, рассмотренный ниже, решает задачу нахождения наибольшего общего делителя двух чисел и за .

Данный алгоритм был впервые описан в книге Евклида "Начала" (около 300 г. до н.э.), хотя, вполне возможно, этот алгоритм имеет более раннее происхождение.

Алгоритм

Сам алгоритм чрезвычайно прост и описывается следующей формулой:

Реализация

int gcd (int a, int b) {

if (b == 0) return a;

else

return gcd (b, a % b);

}

Используя тернарный условный оператор C++, алгоритм можно записать ещё короче:

int gcd (int a, int b) {

return b ? gcd (b, a % b) : a;

}

Наконец, приведём и нерекурсивную форму алгоритма:

int gcd (int a, int b) { while (b) {

a %= b; swap (a, b);

}

return a;

}

Доказательство корректности

Сначала заметим, что при каждой итерации алгоритма Евклида его второй аргумент строго убывает, следовательно, посколько он неотрицательный, то алгоритм Евклида всегда завершается.

Для доказательства корректности нам необходимо показать, что

для

любых .

Покажем, что величина, стоящая в левой части равенства, делится на настоящую в правой, а стоящая в правой — делится на стоящую в левой. Очевидно, это будет означать, что левая и правая части совпадают, что и докажет корректность алгоритма Евклида.

Обозначим 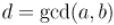. Тогда, по определению, и 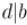. Далее, разложим остаток от деления 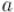на 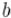через их частное:

Но тогда отсюда следует:

Итак, вспоминая утверждение 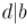, получаем систему:

Воспользуемся теперь следующим простым фактом: если для каких-то трёх чисел		выполнено:	и	,
то выполняется и:	. В нашей ситуации получаем:

Или, подставляя вместо 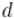его определение как 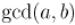, получаем:

Итак, мы провели половину доказательства: показали, что левая часть делит правую. Вторая половина доказательства производится аналогично.

Время работы

Время работы алгоритма оценивается теоремой Ламе, которая устанавливает удивительную связь алгоритма Евклида и последовательности Фибоначчи:

Если и 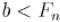для некоторого 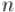, то алгоритм Евклида выполнит не более рекурсивных вызовов.

Более того, можно показать, что верхняя граница этой теоремы — оптимальная. При

будет выполнено именно рекурсивных вызова. Иными словами, последовательные числа Фибоначчи — наихудшие входные данные для алгоритма Евклида.

Учитывая, что числа Фибоначчи растут экспоненциально (как константа в степени 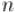), получаем, что алгоритм Евклида выполняется за 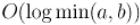операций умножения.

НОК (наименьшее общее кратное)

Вычисление наименьшего общего кратного (least common multiplier, lcm) сводится к вычислению	следующим
простым утверждением:

Таким образом, вычисление НОК также можно сделать с помощью алгоритма Евклида, с той же асимптотикой:

int lcm (int a, int b) { return a / gcd (a, b) * b;

}

(здесь выгодно сначала поделить на , а только потом домножать на 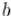, поскольку это поможет избежать переполнений в некоторых случаях)

Литература

● Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: Построение и анализ [2005]

Решето Эратосфена

Решето Эратосфена - это алгоритм, позволяющий найти все простые числа в отрезке		за
операций.
Идея проста — запишем ряд чисел	, и будем вычеркивать сначала все числа, делящиеся на , кроме
самого числа , затем деляющиеся на	, кроме самого числа , затем на , затем на ,	, и все остальные простые
до .

Сразу приведём реализацию алгоритма:

int n; // входные данные vector<char> prime (n+1, true);

prime[0] = prime[1] = false; // если кто-то будет использовать эти значения for (int i=2; i<=n; ++i)

if (prime[i])

for (int j=i+i; j<=n; j+=i) prime[j] = false;

В таком виде алгоритм потребляет 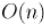памяти и выполняет 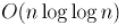действий.

Асимптотика

Докажем, что асимптотика алгоритма равна .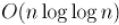

Итак, для каждого простого	будет выполняться внутренний цикл, который совершит	действий.
Следовательно, нам нужно оценить следующую величину: