Алгоритмы C++

else if (a[i][j] == 'T') t_st = i*m+j;

cout << (win[p_st][t_st][true] ? "WIN" : loose[p_st][t_st] [true] ? "LOSS" : "DRAW");

}

Теория Шпрага-Гранди. Ним

Введение

Теория Шпрага-Гранди — это теория, описывающая так называемые равноправные (impartial) игры, т.е. игры,

вкоторых разрешённые ходы и выигрышность/проигрышность зависят только от состояния игры, но не от того, какой игрок ходил. Иными словами, первый и второй игрок различаются только тем, что первый игрок первым совершает ход, а

востальном они равноправны.

Кроме того, предполагается, что игроки располагают всей информацией (в том числе и о положении соперника).

Предполагается, что игра конечна, т.е. при любой игре игроки рано или поздно придут в позицию, из которой нет переходов в другие позиции. Эта позиция является проигрышной для игрока, который должен делать ход из этой позиции. Соответственно, она является выигрышной для игрока, пришедшего в эту позицию. Понятно, ничейных исходов в такой игре не бывает.

Иными словами, такую игру можно полностью описать ориентированным ациклическим графом: вершинами в нём являются состояния игры, а рёбрами — переходы из одного состояния игры в другое в результате хода текущего игрока (повторимся, в этом первой и второй игрок равноправны). Одна или несколько вершин не имеют исходящих рёбер, они является проигрышными вершинами (для игрока, который должен совершать ход из такой вершины).

Поскольку ничейных исходов не бывает, то все состояния игры распадаются на два класса: выигрышные и проигрышные. Выигрышные — это такие состояния, что найдётся ход текущего игрока, который приведёт

к поражению другого игрока даже при его оптимальной игре. Соответственно, проигрышные состояния — это состояния, из которых все переходы ведут в состояния, приводящие к победе второго игрока, несмотря на "сопротивление" первого игрока. Иными словами, выигрышным будет состояние, из которого есть хотя бы один переход в проигрышное состояние, а проигрышным является состояние, из которого все переходы ведут в выигрышные состояния (или из которого вообще нет переходов).

Наша задача — для любой заданной игры провести классификацию состояний этой игры, т.е. для каждого состояния определить, выигрышное оно или проигрышное.

Теорию таких игр независимо разработали Роланд Шпраг (Roland Sprague) в 1935 г. и Патрик Майкл Гранди (Patrick Michael Grundy) в 1939 г.

Игра "Ним"

Эта игра является одним из примеров описываемых выше игр. Однако, как мы увидим чуть позже, любая из рассматриваемых нами игр на самом деле эквивалентна игре "ним" (nim), поэтому изучение этой игры автоматически позволяет нам решать все остальные игры.

Игра "ним" представляет собой следующее. Есть несколько кучек, в каждой из которых по несколько камней (как минимум по одному). За один ход игрок может взять из любой кучки любое строго положительное число камней и выбросить их. Соответственно, когда все кучки опустеют, корректных ходов больше не будет, и текущий игрок проигрывает.

Итак, состояние игры ним однозначно описывается неупорядоченным набором натуральных чисел. За один ход разрешается строго уменьшить любое из чисел (если в результате число станет нулём, то оно удаляется из набора).

Решение этой игры опубликовал в 1901 г. Чарлз Бутон (Charles Bouton).

Теорема. Текущий игрок имеет выигрышную стратегию тогда и только тогда, когда XOR-сумма размеров кучек отлична от нуля. В противном случае текущий игрок находится в проигрышном состоянии. (XOR-суммой чисел

называется выражение , где — операция побитового исключающего или)

Доказательство. Обозначим через

размеры кучек до хода игрока, а через — после

хода. Понятно, что эти два вектора различаются ровно в одном элементе. Обозначим через и XOR-суммы до и после хода игрока, т.е.:

Тогда, по свойству операции , можем записать:

где — номер кучки, в которой совершил ход игрок.

Доказывать теорему будем теперь по индукции. Предполагаем, что теорема верна для всех состояний, в которые мы можем перейти из текущего состояния (поскольку игра ациклична, то это предположение корректно).

Тогда доказательство распадается на две части: если			, то надо доказать, что текущее состояние проигрышно, т.
е. все переходы из него ведут в состояния с		. Если же	, то надо доказать, что найдётся переход,
приводящий нас в состояние с	.

● Пусть . Если из текущего состояния нет переходов, то доказывать нечего (текущее состояние и так проигрышно). Иначе рассмотрим любой переход. Тогда по вышеприведённой формуле получаем для него:

Но поскольку	, то	, что и означает, что новое состояние будет выигрышным, что и требовалось доказать.

● Пусть . Покажем, какой ход надо совершить, чтобы прийти в проигрышное состояние (т.е. с ).

Рассмотрим битовую запись числа . Возьмём старший ненулевой бит, пусть его номер равен						. Пусть — номер того
из чисел		, у которого -ый бит отличен от нуля (такой найдётся, поскольку в их XOR-сумме				этот бит отличен от
нуля). Тогда положим			; утверждается, что это и есть искомый ход.
Сначала надо проверить, что это ход корректный, т.е. что					. Однако это верно, поскольку все биты, старшие -
го, у	и	совпадают, а в	-ом бите у	будет ноль, а у	будет единица.

Теперь посчитаем, какая XOR-сумма получится при этом ходе:

Таким образом, действительно существует ход, приводящий в проигрышное состояние, что и требовалось доказать.

Следствие. Любое состояние ним-игры можно заменить эквивалентным состоянием, состоящим из единственной кучки размера, равного XOR-сумме размеров кучек в старом состоянии.

Эквивалентность любой игры ниму. Теорема Шпрага-Гранди

Здесь мы покажем, как любой (из класса рассматриваемых нами) игре поставить в соответствие ним. Иными словами, любому состоянию любой игры можно поставить в соответствие ним-кучку. Если размер кучки равен нулю, то текущее состояние проигрышно, иначе выигрышно.

Лемма (о ниме с увеличениями). Рассмотрим следующий модифицированный ним: позиция попрежнему задаётся набором натуральных чисел, однако за один ход теперь можно помимо произвольного уменьшения одного из чисел, также увеличивать некоторые из чисел на некоторые указанные величины (но при

этом правила увеличения таковы, что игра остаётся корректной, т.е. никогда не станет бесконечной). Утверждается, что такой модифицированный ним эквивалентен обычному ниму, причём в том же состоянии. Доказательство. Фактически нам надо доказать, что наличие дополнительных увеличивающих ходов ничего не меняет. Действительно, пусть текущее состояние выигрышно; тогда для текущего игрока нет никакого смысла использовать этот ход (ведь если текущий игрок увеличит какое-то из чисел, то второй игрок всегда сможет ответить, уменьшив это число обратно до старого значения). Если же текущее состояние проигрышно, то тем более наличие или отсутствие этого хода ничего не может изменить. Что и требовалось доказать.

Теорема Шпрага-Гранди. Рассмотрим любое состояние		некоторой игры; пусть из него есть переходы
в некоторые состояния	. Утверждается, что состоянию		можно поставить в соответствие кучку
нима некоторого размера	(и эти две игры будут эквивалентны). Более того, это число			можно находить

индуктивно: если мы найдём эти числа для каждого из новых состояний , то равно:

(результатом операции (minimum excludant) от множества чисел является наименьшее неотрицательное число, не встречающееся в этом множестве)

Доказательство. Доказывать теорему будем по индукции: пусть она верна для всех новых состояний . Докажем её для текущего состояния 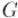. Положим

и докажем, что состояние игры ним с единственной кучкой размера эквивалентно состоянию нашей игры.

Поскольку	определялось как		ним-чисел, соответствующих новым состояниям, то получается, что для
каждого		существует переход из			в некоторое состояние		, которому эквивалентна ним-игра
с единственной кучкой		. Кроме того, по определению операции				, могут существовать и переходы в
состояния, которым соответствуют				.
Таким образом, получается, что состояние				эквивалентно ниму с увеличениями с единственной кучкой размера				:

ведь мы можем произвести любое уменьшение числа , но и, возможно, можем произвести некоторые увеличения. Но по предыдущей лемме, ним с увеличениями эквивалентен обычному ниму в том же состоянии.

Таким образом, состояние	нашей игры эквивалентно ниму с единственной кучкой размера	, что и
требовалось доказать.

Применение теоремы Шпрага-Гранди

Опишем наконец целостный алгоритм, применимый к любой игре (из рассматриваемого нами класса) для определения выигрышности/проигрышности текущего состояния .

Функция, которая каждому состоянию игры ставит в соответствие ним-число, называется функцией Гранди.

● Если из текущего состояния есть переходы в состояния			, то для каждого из них (фактически,
рекурсивно) вычисляем функцию Гранди		. Тогда функция Гранди для состояния			будет равна
	наименьшему неотрицательному числу, не совпадающему ни с одним из чисел			:

●Если текущее состояние представляет собой сумму независимых игр (как, например, ним из нескольких кучек представляет собой сумму нимов из каждой кучки по отдельности), то опять же, вычисляем функцию Гранди

для каждой из этих игр в отдельности. Функция Гранди для состояния будет равна XOR-сумме этих чисел :

Первое применение непосредственно вытекает из теоремы Шпрага-Гранди. Второе применение получается следующим образом: сначала по теореме Шпрага-Гранди каждую из независимых "под-игр" заменяем ним-кучкой; затем по теореме Бутона находим ним-число для нима из этих нескольких кучек.

Также следует отметить следующий момент. Для больших игр, т.е. игр, в которых число состояний слишком велико, чтобы для каждого посчитать функцию Гранди, на помощь приходит следующий факт. Очень часто в выписанных таблицах первых значений функции Гранди можно найти определённые закономерности,

которые сохраняются и для всей бесконечной таблицы. Кроме того, очень часто функция Гранди оказывается периодичной.

Литература

● John Horton Conway. On numbers and games [1979]

Задача Джонсона с одним станком

Это задача составления оптимального расписания обработки деталей на единственном станке, если -ая деталь обрабатывается на нём за время , а за секунд ожидания до обработки этой детали платится штраф .

Таким образом, задача заключается в поиске такого переупорядочения деталей, что следующая величина (размер штрафа) минимальна. Если мы обозначим через перестановку деталей ( — номер первой обрабатываемой детали, — второй, и т.д.), то размер штрафа равен:

Иногда эта задача называется задачей однопроцессорного обслуживания множества заявок.

Решение задачи в некоторых частных случаях

Первый частный случай: линейные функции штрафа

Научимся решать эту задачу в случае, когда все линейны, т.е. имеют вид:

где — неотрицательные числа. Заметим, что в этих линейных функциях свободный член равен нулю, т.к. в противном случае к ответу сразу можно прибавить этот свободный член, и решать задачу с нулевым свободным членом.

Зафиксируем некоторое расписание — перестановку . Зафиксируем какой-то номер			, и
пусть перестановка	равна перестановке , в которой обменяли -ый и	-ый элементы. Посмотрим, на
сколько при этом изменился штраф:

легко понять, что изменения произошли только с -ым и -ым слагаемыми:

Понятно, что если расписание является оптимальным, то любое его изменение приводит к увеличению штрафа (или сохранению прежнего значения), поэтому для оптимального плана можно записать условие:

Преобразуя, получаем:

Таким образом, оптимальное расписание можно получить, просто отсортировав все детали по отношению к в обратном порядке.

Следует отметить, что мы получили этот алгоритм так называемым перестановочным приёмом: мы попробовали обменять местами два соседних элемента расписания, вычислили, насколько при этом изменился штраф, и отсюда вывели алгоритм поиска оптимального расписания.

Второй частный случай: экспоненциальные функции штрафа

Пусть теперь функции штрафа имеют вид:

где все числа неотрицательны, константа положительна.

Тогда, применяя аналогичным образом здесь перестановочный приём, легко получить, что детали надо сортировать в порядке убывания величин:

Третий частный случай: одинаковые монотонные функции штрафа

В этом случае считается, что все совпадают с некоторой функцией , которая является возрастающей. Понятно, что в этом случае оптимально располагать детали в порядке увеличения времени обработки .

Теорема Лившица-Кладова

Теорема Лившица-Кладова устанавливает, что перестановочный приём применим только для вышеописанных трёх частных случаев, и только них, т.е.:

●	Линейный случай:	, где	— неотрицательные константы,
●	Экспоненциальный случай:		, где и — положительные константы,
●	Тождественный случай:	, где	— возрастающая функция.

Эта теорема доказана в предположении, что функции штрафа являются достаточно гладкими (существуют третьи производные).

Во всех трёх случаях применим перестановочный приём, благодаря которому искомое оптимальное расписание может быть найдено простой сортировкой, следовательно, за время .

Задача Джонсона при N = 2

Постановка задачи

Пусть имеется M деталей, которые нужно обработать на двух станках: каждую деталь сначала на первом, а затем на втором станке. Про каждую i-ую деталь известно, что она обрабатывается первым станком за Ai единиц времени,

а вторым станком - за Bi единиц. Кроме того, порядок обработки деталей на первом станке и на втором станке должен совпадать. Требуется найти такой порядок обработки деталей, чтобы потратить наименьшее время.

Математическая модель

Обозначим через Xi время простоя второго станка непосредственно перед началом обработки детали с номером i.

Тогда критерием оптимальности задачи Джонсона при N = 2 станет функционал: F(X) = СУММА Xi => min.

Математическое решение задачи

Расписание обработки деталей на станках задаётся перестановкой R натуральных чисел от 1 до M. Например, при R = (1, 2, ..., M) мы имеем:

X1 = A1

X2 = max ( A1 + A2 - B1 - X1, 0 )

...

и тогда

F(X) = СУММА Xi = max ( A1 + ... + AM - B1 - ... - BM-1,

...,