
Алгоритмы C++
.pdfA1 + ... + Ai - B1 - ... - Bi-1,
..., A1 )
Теперь рассмотрим две перестановки R = (1, 2, ..., i, i+1, ..., M) и Q = (1, 2, ..., i+1, i, ..., M), т.е. поменяли местами детали i и i+1.
Предположим, что F(R) > F(Q). Тогда имеем: max (
A1 + ... + Ai - B1 - ... - Bi-1, A1 + ... + Ai+1 - B1 - ... - Bi,
) > max (
A1 + ... + Ai-1 + Ai+1 - B1 - ... - Bi-1,
A1 + ... + Ai+1 - B1 - ... - Bi-1 - Bi+1,
)
Теперь вычтем из правой и левой частей величину A1 + ... + Ai+1 - B1 - ... - Bi-1. После несложных преобразований получим:
min ( Ai+1, Bi ) < min ( Ai, Bi+1 )
Итак, последнее неравенство выполняется тогда и только тогда, когда F(R) > F(Q), т.е. деталь с номером i+1 должна обрабатываться раньше детали с номером i.
Описание алгоритма решения задачи
Вариант 1.
Сортируем детали, при этом операцию сравнения i-ой и i+1-ой деталей определяем следующим образом: если min ( Ai+1, Bi ) < min ( Ai, Bi+1 ), то деталь с номером i+1 должна идти раньше, иначе - наоборот. Вариант 2. (непосредственно следует из первого варианта)
1. Найти минимальную величину среди всех Ai и Bi.

2.Если минимум достигается на Ai, то деталь с номером i нужно ставить на обработку самой первой. Если же на Bi, то деталь с номером i ставится на обработку самой последней.
3.Найденная деталь исключается из рассмотрения. Переходим к шагу 1.
Этот, второй, вариант алгоритма называется алгоритмом Джонсона.
Сложность алгоритма Джонсона, очевидно, составляет O (N log N) при использовании быстрой сортировки.
Реализация алгоритма Джонсона
Здесь я приведу пример реализации алгоритма Джонсона. Входные данные - Ai и Bi.
Помимо искомого порядка деталей, программа также вычисляет минимальное время, требуемое для обработки всех деталей.
int main()
{
int n; cin >> n;
vector < pair<double,double> > a (n); for (int i=0; i<n; ++i)
cin >> a[i].first >> a[i].second;
vector < pair < double, pair<int,int> > > b; b.reserve (n*2);
for (int i=0; i<n; ++i)
{
b.push_back (make_pair (a[i].first, make_pair (i, 0))); b.push_back (make_pair (a[i].second, make_pair (i, 1)));
}
sort (b.begin(), b.end());
vector<char> used (n); vector<int> res_temp [2];

res_temp[0].reserve (n); res_temp[1].reserve (n); for (int i=0; i<n*2; ++i)
if (!used [ b[i].second.first ])
{
used [ b[i].second.first ] = true;
res_temp [ b[i].second.second ] .push_back (b[i].
second.first);
}
vector<int> result; result.reserve (n);
copy (res_temp[0].begin(), res_temp[0].end(), back_inserter (result)); copy (res_temp[1].rbegin(), res_temp[1].rend(), back_inserter (result));
double time1 = 0, time2 = 0; for (int i=0; i<n; ++i)
{
int cur = result[i]; time1 += a[cur].first; if (time2 < time1)
time2 = time1; time2 += a[cur].second;
}
double res_time = max (time1, time2);
printf ("%.5lf\n", res_time); for (int i=0; i<n; ++i)
printf ("%d ", result[i]+1); printf ("\n");
}

Оптимальный выбор заданий при известных временах завершения и длительностях выполнения
Пусть дан набор заданий, у каждого задания известен момент времени, к которому это задание нужно завершить, и длительность выполнения этого задания. Процесс выполнения какого-либо задания нельзя прерывать до его завершения. Требуется составить такое расписание, чтобы выполнить наибольшее число заданий.
Решение
Алгоритм решения - жадный. Отсортируем все задания по их крайнему сроку, и будем рассматривать их по очереди в порядке убывания крайнего срока. Также создадим некую структуру данных Q, в которую мы будем постепенно помещать задания, и извлекать из структуры задание с наименьшим временем выполнения (например,
можно использовать set или priority_queue). Изначально Q пустая. Пусть мы рассматриваем i-ое задание.
Сначала поместим его в Q. Рассмотрим отрезок времени между сроком завершения i-го задания и сроком завершения (i- 1)-го задания - отрезок некоторой длины T. Будем извлекать из Q задания и помещать на выполнение в этом отрезке, пока отрезок T не станет равным нулю. Важный момент - если в какой-то момент времени очередное извлечённое
из структуры задание можно успеть частично выполнить в отрезке T, то мы выполняем это задание частично - именно настолько, насколько это возможно, т.е. в течение T единиц времени, а оставшуюся часть задания
помещаем обратно в Q. По окончании этого алгоритма мы выберем оптимальное решение (или, по крайней мере, одно из нескольких решений).
Итоговая асимптотика алгоритма - O (N log N).
Реализация
int n;
vector < pair<int,int> > a; // пары крайний срок - длительность
... чтение n и a ...
sort (a.begin(), a.end());
typedef set < pair<int,int> > t_s; t_s s;

vector<int> result;
for (int i=n-1; i>=0; --i) {
int t = a[i].first - (i ? a[i-1].first : 0); s.insert (make_pair (a[i].second, i)); while (t && !s.empty()) {
t_s::iterator it = s.begin(); if (it->first <= t) {
t -= it->first; result.push_back (it->second);
}
else {
s.insert (make_pair (it->first - t, it->second)); t = 0;
}
s.erase (it);
}
}
for (size_t i=0; i<result.size(); ++i) cout << result[i] << ' ';

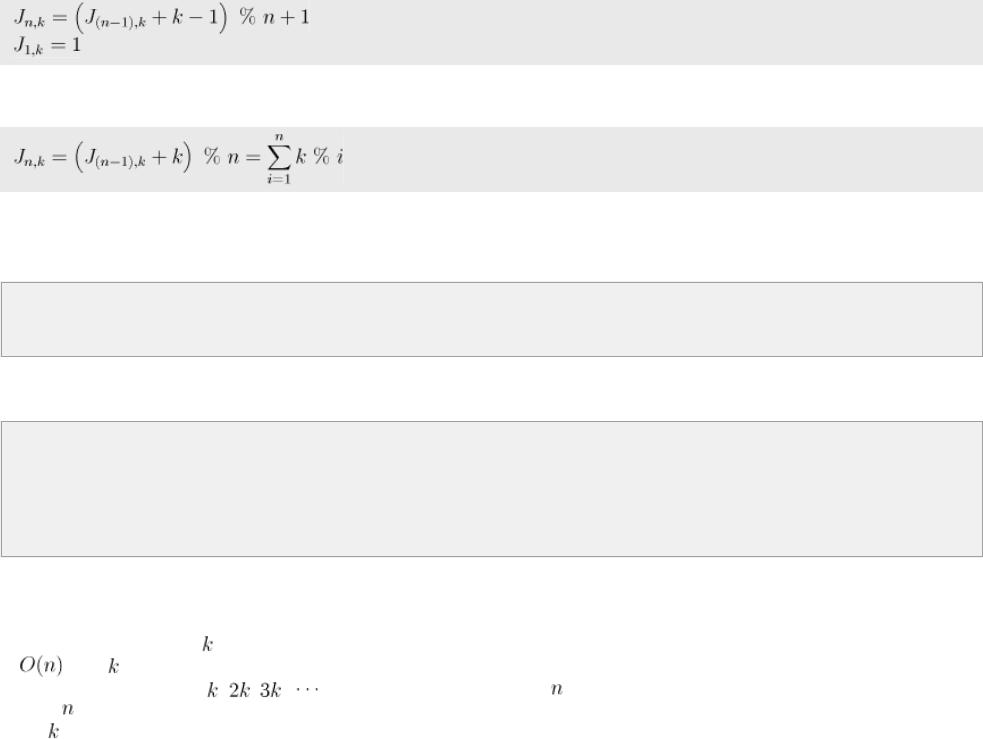
Здесь 1-индексация несколько портит элегантность формулы, если нумеровать позиции с нуля, то получится очень наглядная формула:
Итак, мы нашли решение задачи Иосифа, работающее за 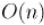 операций.
операций.
Простая рекурсивная реализация (в 1-индексации):
int joseph (int n, int k) {
return n>1 ? (joseph (n-1, k) + k - 1) % n + 1 : 1;
}
Нерекурсивная форма:
int joseph (int n, int k) { int res = 0;
for (int i=1; i<=n; ++i) res = (res + k) % i;
return res + 1;
}
Решение за 
Для сравнительно небольших |
можно придумать более оптимальное решение, чем рассмотренная выше динамика |
|||
за |
. Если небольшое, то даже интуитивно понятно, что тот алгоритм делает много лишних |
|||
действий: рассматривая числа |
, |
, |
, , и лишь только когда он достигнет и совершит переход по кругу |
|
из числа |
в число 1, — только тогда происходят сильные изменения, до этого же алгоритм просто шагает шагами |
|||
длины . Соответственно, попытаемся избавиться от этих ненжных шагов, т.е. научимся удалять сразу все числа, кратные 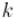 , за одну операцию.
, за одну операцию.
Сложность здесь в том, что после удаления этих чисел у нас получится задача с меньшим 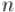 , но стартовой позицией не
, но стартовой позицией не

в первом числе, а, возможно, где-то в другом месте. Поэтому, вызвав рекурсивно себя от задачи с новым 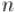 , мы затем должны перевести результат в нашу систему нумерации из его собственной. Впрочем, сложности здесь чисто технические — надо аккуратно и кратко реализовать этот пересчёт.
, мы затем должны перевести результат в нашу систему нумерации из его собственной. Впрочем, сложности здесь чисто технические — надо аккуратно и кратко реализовать этот пересчёт.
Также отдельно надо разбирать случай, когда  станет меньше . В этом случае вышеописанная оптимизация выродится в бесконечный цикл, поэтому для разбора этого случая можно просто взять решение старой динамикой.
станет меньше . В этом случае вышеописанная оптимизация выродится в бесконечный цикл, поэтому для разбора этого случая можно просто взять решение старой динамикой.
Реализация (для удобства в 0-индексации):
int joseph (int n, int k) { if (n == 1) return 0; if (k == 1) return n-1;
if (k > n) return (joseph (n-1, k) + k) % n; int cnt = n / k;
int res = joseph (n - cnt, k); res -= n % k;
if (res < 0) res += n; else res += res / (k - 1); return res;
}
Оценим асимптотику этого алгоритма. Сразу заметим, что случай |
разбирается у нас старым |
решением, которое отработает в данном случае за . Теперь рассмотрим сам алгоритм. Фактически, на каждой
его итерации вместо чисел мы получаем примерно |
чисел, поэтому общее число итераций |
алгоритма примерно можно найти из уравнения:
логарифмируя его, получаем:

пользуясь разложением логарифма в ряд Тейлора, получаем приблизительную оценку:
Таким образом, асимптотика алгоритма действительно 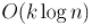 .
.
Аналитическое решение для
В этом частном случае (в котором и была поставлена эта задача Иосифом Флавием) задача решается значительно проще.
В случае чётного  получаем, что будут вычеркнуты все чётные числа, а потом останется задача для , тогда ответ для
получаем, что будут вычеркнуты все чётные числа, а потом останется задача для , тогда ответ для 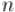 будет получаться из ответа для
будет получаться из ответа для  умножением на два и вычитанием единицы (за счёт сдвига позиций):
умножением на два и вычитанием единицы (за счёт сдвига позиций):
Аналогично, в случае нечётного 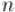 будут вычеркнуты все чётные числа, затем первое число, и останется задача для
будут вычеркнуты все чётные числа, затем первое число, и останется задача для  , и с учётом сдвига позиций получаем вторую формулу:
, и с учётом сдвига позиций получаем вторую формулу:
При реализации можно непосредственно использовать эту рекуррентную зависимость. Можно эту закономерность перевести в другую форму: представляют собой последовательность всех нечётных
чисел, "перезапускающуюся" с единицы всякий раз, когда  оказывается степенью двойки. Это можно записать и в виде одной формулы:
оказывается степенью двойки. Это можно записать и в виде одной формулы:
Аналитическое решение для 
Несмотря на простой вид задачи и большое количество статей по этой и смежным задачам, простого аналитического представления решения задачи Иосифа до сих пор не найдено. Для небольших выведены некоторые формулы, но, по-видимому, все они трудноприменимы на практике (например, см. Halbeisen, Hungerbuhler "The Josephus Problem" и Odlyzko, Wilf "Functional iteration and the Josephus problem").

Игра Пятнашки: существование решения
Напомним, что игра представляет собой поле на , на котором расположены фишек, пронумерованных числами от до , а одно поле оставлено пустым. Требуется, передвигая на каждом шаге какую-либо фишку на свободную позицию, прийти в конце концов к следующей позиции:
Игру Пятнашки ("15 puzzle") изобрёл в 1880 г. Нойес Чэпман (Noyes Chapman).
Существование решения
Здесь мы рассмотрим такую задачу: по данной позиции на доске сказать, существует ли последовательность ходов, приводящая к решению, или нет.
Пусть дана некоторая позиция на доске:
где один из элементов равен нулю и обозначает пустую клетку 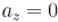 . Рассмотрим перестановку:
. Рассмотрим перестановку:
|
|
|
|
|
(т.е. перестановка чисел, соответствующая позиции на доске, без нулевого элемента) |
|
|
||
Обозначим через |
количество инверсий в этой перестановке (т.е. количество таких элементов |
и , что |
, |
|
но |
). |
|
|
|

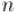 и . По кругу выписывают все натуральные числа от 1 до
и . По кругу выписывают все натуральные числа от 1 до 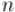 . Сначала отсчитывают -ое число, начиная с первого, и удаляют его. Затем от него отсчитывают чисел и -ое удаляют, и т. д. Процесс останавливается, когда остаётся одно число. Требуется найти это число.
. Сначала отсчитывают -ое число, начиная с первого, и удаляют его. Затем от него отсчитывают чисел и -ое удаляют, и т. д. Процесс останавливается, когда остаётся одно число. Требуется найти это число.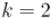 ).
).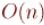
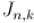 через решение предыдущих задач. С помощью моделирования построим таблицу значений, например, такую:
через решение предыдущих задач. С помощью моделирования построим таблицу значений, например, такую: