Вопрос 3.2

Асимптотой графика функции у =¦( х) называется прямая, обладающая следующим свойством, что расстояние от переменной точки на графике до этой прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.

Теорема 1. Пусть функция у = ¦( х) определена в некоторой окрестности точки х₀ (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х® х₀ – 0 (слева) или при х® х₀ + 0 (справа) – равен бесконечности, тогда прямая при х = х₀ является вертикальной асимптотой графика функции у = ¦( х).

Замечание. Вертикальные асимптоты следует искать в точках разрыва функции у = ¦( х) или на концах ее области определения (а, b) если а и b - конечные числа.

Теорема 2. Пусть функция у = ¦(х) определена при достаточно больших х и существует конечный предел функции при х ® ¥ и он равен числу b. Тогда прямая у = b есть горизонтальная асимптота графика функции у = ¦( х).

Замечание. Если конечен лишь один из пределов слева или справа, то функция имеет лишь левостороннюю или правостороннюю асимптоту.

Теорема 3. Пусть функция у = ¦( х) определена при достаточно больших х и существует конечные пределы

Тогда прямая у = kx + b является наклонной асимптотой. Тогда прямая у = kx + b является наклонной асимптотой.

Вопрос 4 Непрерывность функции

Определение 1. Функция ¦(х) называется непрерывной в точке х₀, если она удовлетворяет следующим трем условиям:

1) определена в точке х₀ (т.е. существует ¦(х₀));

2) имеет конечный предел функции при х ® х₀;

3) этот предел равен значению функции в этой точке , т.е.

Определение 2. Функция у =¦(х) называется непрерывной в точке х₀, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: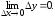

Теорема. Сумма, разность, произведение и частное двух функций непрерывных в одной и той же точке а, есть функция непрерывная в той же точке, причем в случае частного предполагается, что функция делитель не обращается в нуль при х = а. (Теорема остается верной для суммы и произведения любого конечного числа функций).

Функция у = ¦(х) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.

Доказано, что все элементарные функции непрерывны в области их определения.

Вопрос 5 точки разрыва первого и второго урода-рода гг…

Точка х₀, в которой функция ¦(х) не является непрерывной называется точкой разрыва.

Точка х₀ называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции слева или справа при х ® х₀, не равные друг другу, либо если они равны между собой, но не равны значению функции в точке х₀.

Обозначим

а) в этом случае функция имеет скачок

б) но не равно значению функции в точке х₀ , имеем устранимый разрыв.

Точка х₀ называется точкой разрыва второго рода, если хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.