моделирование инфоком / Полный Курс лекций по Моделирование ИнфКом Систем

Критерий согласия Пирсона

В критерии согласия Пирсона сравниваются между собой теоретические и эмпирические числа попаданий в интервалы.

Возьмѐм те интервалы, по которым была построена гистограмма. Эмпирические числа попаданий в эти интервалы nj сравниваем с теоретическим числом попаданий npj, где pj – вероятность попадания нашей величины в j-й интервал.

Теоретическое распределение можно считать подобранным верно на уровне значимости p, если суммарная квадратичная относительная разность между теоретическим и практическим числом попаданий в каждый интервал будет не очень большой, т.е. должно выполняться условие:

k n		j	np	j	2		k L .
					2
						1 p
			np j
j 1
где
―k - L‖			- число степеней свободы,

L – число независимых условий, наложенных на частоты pj , например: а) условие p j 1;

б) условие совпадения теоретического среднего значения и экспериментального; в) условие совпадения теоретической дисперсии и экспериментальной, и т. д.

Чаще всего L = 3. Чем больше число степеней свободы, тем больше случайная величина 2 подчиняется распределению Пирсона.

При использовании данного критерия следует учитывать, что он дает достоверные результаты для случая, когда все npj 5.

Для удобства расчетов строится таблица результатов, в которую заносятся: номера интервалов, границы интервалов aj и bj, практическое число попаданий nj, вероятность попадания в интервал pj, теоретическое число попаданий npj и величины (nj npj)2/npj .

Вероятность попадания в j-й интервал подсчитывается по формуле p j Fx bj Fx a j .

Проверяется выполнение условия все npj 5, и объединяются те интервалы, в которых npj<5.

Перестраивается таблица и подсчитывается статистика Пирсона. На последнем этапе сравнивается полученная величина с квантилем 2-распределения Пирсона на заданном уровне значимости.

Замечание. В целом, с помощью критерий согласия, можно опровергнуть выбранную гипотезу, если же условие критерия при выбранном уровне значимости выполняется, то это не может служить доказательством правильности гипотезы, а указывает лишь на то, что гипотеза не противоречит данным эксперимента.

111

Пример. Результаты опроса общественного мнения говорят о том, что наибольшей популярностью покупателей пользуются мужские пальто серого цвета (30% опрошенных), затем пальто черного цвета (26% опрошенных), синего (22%) и коричневого (22%). Имеется ли существенная разница между цветами пальто с точки зрения покупателей, если считать, что результаты получены 1) при n=100, 2) при n=1000?

Применим критерий хи-квадрат при уровне значимости =0.05. Здесь проверяется гипотеза о принадлежности данных опроса к равномерному распределению. Число интервалов K=4.

При n=100 имеем значения частот n1 = 0.3· n =30, n2 =26, n3 =22, n4 =22; вероятности pi (i =1,..., 4) для равномерного распределения равны 0.25; теоретические частоты npi =

100∙0.25 =25; критическое значение с числом степеней свободы r =(4-2-1)=1, равно 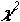0.95 = 3.8, значение критерия

,

поэтому гипотеза о принадлежности данных опроса к равномерному распределению принимается.

При n=1000 значение критерия

,

поэтому гипотеза о принадлежности распределения популярности пальто различного цвета к равномерному распределению должна быть отвергнута. В этом случае имеет смысл упорядочить все цвета мужских пальто по уровню спроса.

Регрессионные модели

Определение коэффициентов модели по экспериментальным данным

Достаточно часто встречаются случаи, когда сложно, а иногда и невозможно теоретически определить зависимость функции выхода от внутренних параметров. В таких случаях решение задачи возможно лишь с помощью эксперимента.

Показатель свойства, для которого нужно построить модель, называют выходным (наблюдаемым) параметром или откликом.

Параметры, от которых зависит этот отклик, называются факторами.

Эксперимент, в котором наблюдатель только измеряет значения факторов, называется пассивным.

Эксперимент, в котором наблюдатель задаѐт значения факторов, называется активным.

При активном эксперименте можно составить такие планы, которые упрощают процедуру определения коэффициентов модели. Исходная формула для определения коэффициентов одна т та же, но при определенных планах она существенно упрощается

112

настолько, что коэффициенты можно считать в ручную. Составлением таких планов занимается теория планирования эксперимента.

Задача состоит в определении зависимости выходного параметра от факторов: y f x1 , x2 ,...,xn .

Знак приближенного равенства стоит по причине возможного влияния других факторов, не вошедших в функцию f. В таком случае можно записать:

y f x1 , x2 ,...,xn ,

где ε – случайная составляющая.

Стараются строить такие модели, чтобы M y f x1 , x2 ,....,xn .

Модель, в которой это равенство выполняется, называется регрессионной, функция f

– функцией регрессии.

Мы будем пользоваться понятием регрессионная модель и в случае, если строгого равенства не получается, имея в виду стремление к нему.

В общем виде, без каких-либо предположений, функцию регрессии определить не удается. Предполагается, что она имеет вид

n

y b0 b1 f 1 (xi ) b2 f2 (xi ) ....,bn fn (xi ) bj f j (xi ) ,

j 0

где fj - функции от факторов, причем f0 = 0; bj – неизвестные коэффициенты.

Если ничего о функциях fj неизвестно, то обычно полагают, что достаточно учесть факторы, их квадраты и произведения между собой.

Так при двух факторах модель может иметь следующий вид:

y b0 b1 x1 b2 x2 b11x12 b22 x22 b12 x1x2 .

Характер зависимостей fj(xi) может быть известен, например: f1(x1)=sin(ax1), f2(x2)=ex2, f3(x3)=ln(x3) и т.д.

В итоге задача сводится к определению неизвестных коэффициентов bj. Результаты эксперимента сводят в таблицу.

Опыт		Факторы				Функции fj			y
	x1	x2	…	xn	f1	f2	…	fn
1	x11	x12		x1n	f11	f12		f1n	y1
2	x21	x22		x2n	f21	f22		f2n	y2
3	x31	x32		x3n	f31	f32		f3n	y3
.				.
.				.
.				.
N	xN1	xN2		xNn	fN1	fN2		fNn	yN

113

Наблюдаемыми величинами являются факторы и выходной параметр y. Функции fj вычисляются по известным зависимостям от xi.

Коэффициенты bj должны быть такими, чтобы модельные значения y (вычисляемые по модели) мало отличались от наблюдаемых.

Наиболее часто для определения коэффициентов bj используют критерий минимума суммы квадратов невязок:

N			2
		n
		оценки
R yi		bj fij		min .
i 1		j 0
		невя зка

Значения коэффициентов bj, удовлетворяющих заданному критерию, можно найти из системы уравнений:

	R	0	R	0		R	0 .
	b		b			b
	0		1			n

В результате дифференцирования получим систему уравнений

N			n				0
	y			b	f	f
			j		ij	i0
i
i 1			j 0
N			n
			bj		fij		0
yi						fi1
i 1			j 0
N			n
yi			bj		fij	fi n	0
			j 0
i 1

Введѐм обозначения:

n

N

N

bj fij

fi0

fi0 yi

j 0

i 1

i 1

n

N

N

b

j

f

ij

f

i n

f

i n

y

i

i 1

i 1

j 0

b
	0
b			B
	1
bn

	y
	1
y2			Y
yN

	f10	f11		f1n
	f20	f21		f
					2n		F0 F1....Fn F .
	f N 0	f N1
				f Nn

В новых обозначениях последнюю систему уравнений можно записать в следующем виде:

n

T

Fj

T

Y

T

n

T

bj F0

F0

F0

bj Fj

YF0

F T F B Y F T

j 0

j 0

0

0

....................

....................

.......................... ,

n

T

Fj

T

Y

T

n

T

F T F B Y F T

bj Fn

Fn

Fn

bj Fj

YFn

n

n

j 0

j 0

или в матричном виде F T FB F T Y .

Отсюда получим вектор искомых коэффициентов B F T F 1 F T Y ,

где F T F - информационная матрица.

114

Пример.

Требуется определить коэффициенты модели y b0 b1 x b0 f0 b1 f1 при следующих результатах наблюдений:

x	f0	f1	y
0	1	0	1
0	1	0	2
1	1	1	3
1	1	1	4

Решение.

Исходя из таблицы исходных данных, матрица значений базовых функций, ее транспонированный вид и информационная матрица будут равны соответственно:

	1	0
						1				1			4		2
F	1 0			F	T			1	1		F	T
													F
	1 1						0	0	1	1				2	2
		1
	1

Проведя несложные матричные операции, получим следующее:

		1					1		a			a				1		2		2			1			1
F T F										11			12											2			2
							T
						F		F								4			2	4			1			1
									a21			a22
											1														2
		1			1 1 1						2			10
F	T
		Y
			0		0 1 1						3			7
											4

В итоге вектор искомых коэффициентов будет иметь следующий вид:

	1	2		1	2		10			1,5
B												.
	1			1				7			2
			2

Таким образом, искомая модель имеет вид y 1,5 2x .

Проверка адекватности модели

Очевидно, что после получения модели необходимо определить насколько, полученная зависимость отражает реальную систему или исследуемое явление, другими словами – проверить адекватность модели. При этом нужно учитывать влияние случайных возмущений на выходную величину y.

В случае отсутствия таких возмущений опыты полностью повторяемы, т.е. при одном и том же наборе факторов выходная величина должна получиться одной и той же.

Отклонение выходной величины (если есть) объясняется наличием случайных выбросов (промахов), появившихся по причине грубых ошибок при измерении.

115

В этом случае адекватность модели можно проверить по отклонениям модельных значений от реальных, причем проверить модель необходимо и в других точках измерений при других значениях факторов (смотри рис. 8.2).

y

модель

реальная

зависимость

x

x2

Дополнительная точка для проверки адекватности

Рис. 8.2 Проверка адекватности

При наличии существенных отклонений обычно повторяют опыты при соответствующих значениях факторов, а также задаются другими значениями факторов из заданного диапазона и сравнивают модельные и реальные значения при этих факторах.

При подтверждении существенных отклонений модель необходимо изменить, причем эксперимент повторять необязательно и можно использовать для ее построения уже имеющиеся данные.

Для принятия решения об адекватности надо иметь в виду, что число опытов должно быть больше числа неизвестных, в противном случае можно принять ошибочное решение. Очевидно, что тем больше число опытов тем лучше для проверки адекватности.

При наличии случайных возмущений для проверки адекватности требуется неоднократное повторение каждого опыта. При этом определяется среднее значение выходной величины для каждого опыта. Отличие средних значений от модельных в какой-то степени характеризует адекватность, но простое сравнение еще не дает основания для принятия решения.

Наиболее адекватной является модель, проходящая через математические ожидания M [ yi ] т.е. регрессионная модель (см.рис. 8.3).

y

Матожидания	Модель, полученная из эксперимента
	Регрессионная

Рис. 8.3.Регрессионная модель

Обычно от модели не требуется, чтобы она точно проходила через математические ожидания и при проверке адекватности можно ограничиться ответом на вопрос: есть ли

116

основание утверждать, что модель не проходит через математические ожидания выходной величины в точках измерений? Если оснований нет, то модель считается достаточно адекватной. В противном случае модель необходимо пересмотреть.

На поставленный вопрос можно получить ответ при известных дисперсиях выходного параметра относительно математических ожиданий в точках измерений и относительно модели.

Если дисперсии равны, то и точки, относительно которых определяются, дисперсии близки.

Таким образом, расхождение дисперсий и позволяет ответить на поставленный вопрос, а значит принять решение об адекватности. Проблема состоит в том, что сами дисперсии не известны, а по опытным данным можно определить только их оценки.

Таким образом, вопрос свелся к следующему: есть ли основание по известным оценкам дисперсий, утверждать, что дисперсии не совпадают?

На этот вопрос дается ответ в математической статистике в рамках теории проверки гипотез (при некотором допущении относительно распределения случайной величины yi).

Решается эта задача следующим образом:

1)выдвигается гипотеза о том, что дисперсии совпадают;

2)рассматривается статистика, равная отношению оценок дисперсий и строится для него плотность распределения (для нормального распределения случайной величины yi это распределение Фишера) при условии, что гипотеза справедлива;

3)задается уровень значимости α – вероятность того, что гипотеза, при ее верности, ошибочно отвергается. Этой вероятности в области возможных значений отношения оценок дисперсий соответствует так называемая критическая область. Гипотеза отвергается при попадании в критическую область, так как это область больших расхождений (обычно в числителе ставят ту оценку, которая больше);

4)по значению отношения оценок дисперсий гипотеза принимается или отвергается:

S 2 ост	F	( f		, f		) ,
S 2 вoc
	1		ост		вос

где F1 ( fост , fвос ) - квантиль распределения Фишера.

Таким образом, если неравенство выполняется, то принимается решение об адекватности математической модели (точнее нет оснований отвергнуть полученную модель).

Оценки дисперсий определяются следующим образом.

Оценка дисперсии относительно математических ожиданий M [ yi ] называется

дисперсией воспроизводимости:

			N	mi
	S 2 вос	1	yij			y	i 2 ,
		fвос
			i 1	j 1

где yij – значение выходного параметра в i-той точке при j-том его повторении,

117

		1	mi
	yi		yij - среднее значение выходного параметра в i-той точке,
		m j 1

mi – число повторений в i-той точке, N – число различных опытов,

fвос – число степеней свободы.

Число степеней свободы определяется как разность общего числа измерений и числа опытов:

N

fвос mi N .

i 1

До определения средних значений число степеней свободы равнялось общему числу измерений, затем для определения средних значений их пришлось связать N уравнениями. Осталось fвос – число степеней свободы.

Дисперсия воспроизводимости характеризует произвольное изменение тех факторов, которые оказывают влияние на выходной параметр, но при испытаниях не измеряются.

Оценка дисперсии относительно модели называется остаточной дисперсией:

		1	N	mi
	Sост		yij		yмi 2 ,
		fост
			i 1	j 1

где fост – число степеней свободы, равное разности общего числа измерений и числа неизвестных параметров модели (n+1, т.е. столько должно быть уравнений для определения параметров, которые связывают опыты):

N

fост mi n 1 .

i 1

Остаточная дисперсия характеризует точность построения математической модели.

Пример.

Пусть N=5, k=3, m1 .... m5 3 .

Модель имеет вид: y b0 b1x1 b2 x2 b3 x3 b11x12 b22 x22 b33x32 ,

Значения оценок дисперсии воспроизводимости и остаточной дисперсии равны соответственно:

		5			3
			yij					i 2
							y
S				i 1	j 1				,
	вос
					5 3 5
		5			3
				yij yмi 2
S				i 1	j 1					.
	ост
					5 3	7

При 0,05, F1 (8,10) 3,07.

118

Если в результате практических расчетов условие

S 2 ост ,

S 2 вос

3,07

выполнится, то принимается решение об адекватности математической модели, при выбранном уровне значимости.

Лекция 9. Планирование экспериментов

Цель лекции: ознакомить обучающихся с порядком планирования активных факторных экспериментов. Раскрываются особенности активных факторных экспериментов, понятие плана эксперимента, указываются общие требования, предъявляемые к планам. Подробно описываются полные факторные и дробные эксперименты, свойство ортогональности плана, которое дает возможность использовать при расчете коэффициентов модели упрощенную формулу.

Определение коэффициентов модели при ортогональных планах

Планом называют задание количества опытов, числа повторений каждого опыта и задание значений факторов в каждом опыте.

Общим требованием к планам является требование неодинаковости, а точнее непропорциональности значений факторов. В противном случае нельзя почувствовать их

раздельное влияние. Математически это приведет к тому, что при одинаковых функциях
от этих факторов, например f1 = x1 , f2 = x2 , определитель F T F X T X			будет равен
нулю, и обращать в этом случае матрицу нельзя.
В активном факторном эксперименте функции fi равны в основном самим факторам,
	1	F T Y эквивалентен записи через X , т.е.
и в этом случае вектор коэффициентов В F T F
1	X T Y .
B X T X

При близких значениях факторов определитель будет близок к нулю. Такие матрицы называют плохо обусловленными. Решение в этих случаях будет сильно зависеть от погрешностей задания факторов, т.е. маленькие ошибки в Х будут приводить к большим ошибкам в определении коэффициентов вектора В. Поэтому значения разных факторов нужно задавать в разных сочетаниях. В ряде случаев планы могут быть составлены так, что вычисление вектора В значительно упрощается.

Рассмотрим такие планы.

Обозначим Gi – число различных уровней i-го фактора.

Эксперимент, в котором уровни каждого фактора комбинируют со всеми уровнями других факторов, называется полным факторным экспериментом (ПлФЭ).

ПлФЭ записывают в виде G1G2 ….GK, при одинаковом количество уровней для каждого фактора ПлФЭ представляют в виде GK.

Эксперимент, в котором число опытов N G1G2 ….GK называют неполным

(дробным) факторным экспериментом.

119

Выбор числа уровней факторов обычно определяется видом математической модели. Например, для линейной модели достаточно варьировать факторы на двух уровнях. Для построения нелинейных моделей число уровней может быть увеличено.

Для построения плана применяют кодированные факторы, меняющиеся от –1 до +1 , так что при двух уровнях фактор принимает значения –1 и +1. Кодированное значение фактора получается из реального путем преобразования по формуле

x2 i max min ,

imax min

где i – значение фактора xi,

χmin и χmax – минимальное и максимальное значения фактора xi. Покажем, как получена данная формула.

Отрезки [x, -1] и [χ, χmin] должны быть пропорциональны:

x ( 1)	1 ( 1)			.
			min
	max min

После очевидных преобразований можно перейти к искомому выражению:

x	2			2	2 max min		, что и требовалось показать.
			min
	max min				max	min

После построения модели можно перейти к прежним реальным факторам:

	max min	(x 1)		.
			min
2
Пример.
Рассмотрим полный факторный план 22, т.е. эксперимент их 4 опытов над 2
факторами.
Таблица плана имеет следующий вид:
					x0	x1	x2
					+1	-1	-1
					+1	+1	-1
					+1	-1	+1
					+1	+1	+1

При добавлении третьего фактора (эксперимент станет 23) таблица удлиняется вдвое и может быть построена следующим образом: третий фактор записывается со значением - 1, а затем таблица для двух факторов копируется для значения +1 третьего фактора:

x1	x2	x3
-1	-1	-1
+1	-1	-1
	120