Q xk ak ei Q xk ak ei ,i , ,...,n,	(3.13)
					ak
где ak – величина			пробного шага на k-ом шаге поиска,				часто
ak const,e,...,en	- координатные орты единичного вектора.
Здесь Q xk	ak ei – измеренное (или вычисленное) значение функции в
точке xk ak ei .

Оценка (3.12) имеет меньше число пробных экспериментов по сравнению с (3.13), но неэффективную оценку градиента, а соответственно и неудовлетворительную работоспособность в зоне экстремума. Оценка (3.13) лишена этих недостатков, но имеет удвоенное число пробных экспериментов.

3.5.Квадратичные методы оптимизации

Сделаем предположение, что в окрестностях экстремума любая функция может быть аппроксимирована квадратичной функцией вида

Q(x) Q bT x xT Aх ,

(3.14)

где Q – константа, b – вектор, А – положительно определенная симметрич-

ная матрица.

Ее градиент в точке экстремума

gradQ x Q x b Ax ,

(3.15)

x

откуда

x A b .

Если в некоторой точке xk

функция (3.14) непрерывна, то она может

быть аппроксимирована в точке xk

функцией (разложение в ряд Тейлора)

Q(x) Q xk x xk T gradQ xk x xk T A xk x xk ,

(3.16)

, так как Q xk

где A x

k

– матрица Гессе, вычисленная в точке x

k

A x

k

.

x xT

Если взять производную по x x xk от функции (3.16), то для точки

x x

k

имеем

gradQ xk A xk xk xk ,

откуда x

k

x

k

A x

k

gradQ x

k

или в более удобной форме

xk xk

k рk ,

(3.17)

40

			Q xk		gradQ xk для задачи минимизации.
где рk
	x xT

Для квадратичной функции n переменных вида (3.14) наилучшим направлением является направление, сопряженное с предыдущим направлением поиска. Говорят, что два направления рk и рk сопряжены относительно

симметричной положительно определенной матрицы А, если

xTk Axk .

Можно показать, что если p , p ,...,pn , есть n взаимно сопряженных

направлений в n-мерном пространстве, то они линейно независимы. Рассмотрим некоторые квадратичные методы оптимизации.

Метод Ньютона. Итерационный процесс организуется в соответствии с выражением (3.17).

Один из подходов выбора k – скаляр для задач минимизации: 1) полагаем и вычисляем x xk рk ;

2) вычисляем Q(x) Q xk рk ;

3) производим проверку неравенства

Q(x) Q xk gradQ xk ,рk , / ;

4) если это неравенство не выполняется, то производим дробление до выполнения этого неравенства.

Методы Ньютона обеспечивают высокую скорость движения для квадратичных поверхностей, у которых существует обратимая ограниченная матрица вторых производных. Количество же вычислений по сравнению с рассмотренными градиентными, за счет вычисления вторых производных и обращения значительно больше.

Метод сопряженных градиентов [3] – разновидность методов сопря-

женных направлений. Эффективный метод оптимизации гладких функций, особенно квадратичных.

Идея метода для задач минимизации. В начальной точке вычисляем градиент и движемся в направлении антиградиента до достижения точки x ,

где целевая функция достигает минимума в выбранном направлении. Вычисляем в точке x градиент и в направлении, сопряженном предыдущему и

представляющем собой линейную комбинацию направления градиента и предыдущего направления, опять движемся до минимума и т.д.

41

xk

рk

k

xk k рk ,	k min Q xk рk ,	k , ,...,	р ,

gradQ xk k рk ,

gradQ xk T gradQ xk gradQ xk .grad xQ xk T рk

Для квадратичных объектов поиск сходится к цели за n-шагов поиска, т.к. в n-мерном пространстве можно построить ортогональную систему n- векторов.

Данный метод не требует вычисления вторых частных производных, имеет высокую скорость сходимости, но весьма чувствителен к погрешностям вычислений.

Метод Давидона-Флетчера-Пауэлла не требует вычисления на каждом шаге поиска обратного гессиана A xk , т.к. направление поиска определяется направлением Hk gradQ xk .

Процедура поиска [5]:

1) на шаге k имеются точка xk и положительно определенная симметрическая матрица H k (обычно в начале поиска единичная или любая сим-

метрическая положительно-определенная матрица);

2) рассчитаем направление рk Hk gradQ xk , (поиск минимума);

3) поиск оптимального шага k путем одномерного поиска функции

Q xk k рk ;

4) положить Vk k рk ;

5) положить xk xk Vk ;

6) найти (рассчитать) Q xk и gradQ xk . Завершить процедуру,

если gradQ xk или Vk достаточно малы. Иначе к п. 7). Замечание

gradQ xk T Vk ;

7)положить Uk gradQ xk gradQ xk ;

8)обновить матрицу H

/ V TU

Hk Hk Gk Bk

,

где G V V T

k

, B H

U

U T H

k

/ U T H

U

k

;

k

k k

k

k

k

k

k

k k

9)

положить k k и перейти к п. 2).

Процесс будет устойчив, если функция Vk

убывает и величина k по-

ложительна. Поскольку

gradQ xk есть направление наискорейшего возрас-

тания, функция Vk будет убывать тогда, когда произведение

V T gradQ x

k

grad T Q x

k

V

k

grad T Q x

k

H

k

gradQ x

k

положи-

k

k

тельно.

42

Это справедливо, если H k – симметрическая положительно определенная матрица для любого k. Начальная матрица H обладает этими свойства-

ми по определению. Процесс обновления сохраняет симметричность гессиана.

При использовании метода для квадратичной функции с симметрической положительно определенной матрицей А, имеем Hn A и поиск ми-

нимума закончится за n шагов.

Метод очень эффективен при оптимизации большинства функций независимо от того, квадратичны они или нет.

Подобные методы реализованы в стандартных процедурах Mathcad. Рассмотрим оптимизацию некоторых функций многих переменных без

ограничений (рис. 3.7).

Для ORIGIN=1

Q1(x1 x2 x3) (x1 3)2 (x2 3)2

(x3 3)2

x1 0

x2 0

x3 0

-начальная точка пои с ка

3

Q1 x01x02x03 0

x0 MaximizeQ1( x1 x2 x3)

x0

3

x-вектор

3

1

3

0

-начальная точка пои с ка

n 3

a 1

xx

3

x

0

1

3

0

n

Q(x)

2

ai xi

xxi

i 1

3

xv MaximizeQ( x)

xv 3

Q(xv) 0

3

Функция Розенброка

QR(x1 x2) 100 x2 x12 2

(1 x1)2

x1 0

x2 0

-начальная точка пои с ка

xr MinimizeQR( x1 x2)

1

QR xr xr

2.004

10

xr

10

1

1

2

Функция " изогнутый гребень"

3

2

QG(x1 x2) 0.3 x12 0.7 x22 exp 1

0.6 (x1 x2) 0.3 x12 0.7 x22

x1 0

x2 0

Рис. 3.7. Решение задач безусловной оптимизации стандартными процедурами Mathcad

43

xg MinimizeQG( x1 x2)			xg		0			QG xg		xg		0
					0				1		2
Многоэкс тремальная функция
Q2(x1 x2) 0.3 x12 0.7 x22			3						0.3 x12 0.7 x22					2
			exp 1			0.6 (x1 x2)
x1 0	x2 0
					0					1	2
xm MaximizeQ2( x1 x2)			xm										0
								Q2 xm xm
					0
Другая начальная точка поис ка
x1 5	x2 5			1.789
									1		2
xm MaximizeQ2( x1 x2)		xm										4.953
								Q2 xm		xm
				0.767
Функция Пауэлла
f(x1 x2 x3 x4) (x1 10 x2)2 5 (x3 x4)2								(x2 2 x3)4			10 (x1 x4)4
x1 0	x2 1	x3 0	x4 1
								0.034
								3.341 10 3
xh Minimizef( x1 x2 x3 x4)					xh
								0.049
								0.057

f xh1xh2xh3xh4 3.845 10 4

Точное решение x=(0,0,0,0)

Рис. 3.7. Окончание

В системе Matlab квадратичные методы оптимизации использованы в функции fminunc, обеспечивающей безусловный поиск минимума гладких функций. Для ускорения процесса поиска в описание функции желательно включить формулы для вычисления градиента и гессиана. Об этом необходимо сообщить в списке управляющих параметров options.

Если целевая функция формируется путем свертки компонентов векто-

ра (или матрицы), например, сепарабельных функций вида n i i* 2 ,

Q x x

i 1

можно воспользоваться функцией lsqnonlin, либо fminimax.

Рассмотрим работу функций на примере рассмотренных функций (рис.

3.7).

44

%Безусловная оптимизация function ris38

clear all x01=[0;0;0];

[x,Q1]=lsqnonlin(@q,x01)

[x,Q1]=fminimax(@q,x01)

[x,Q1]=fminunc(@q,x01) X0=-3:0.1:3;Y0=-2:0.1:5; [X,Y]=meshgrid(X0,Y0); s=size(X);Z=zeros(s); for i=1:s(1)

for j=1:s(2) Z(i,j)=Rosenbrock([X(i,j);Y(i,j)]);

end

end axes('Xlim',[-3,3],'Ylim',[-2,5]); axis equal;grid off;hold on; v=1:2:10;V=10:4:20; contour(X,Y,Z,[v V]); xlabel('x1');ylabel('x2')

options=optimset('Display','final','GradObj','on','Hessian','on'); x0=[-2;2];

line(x0(1),x0(2),'Marker','.','MarkerSize',10);

%[x,Q,e_flag,out,grad,hes]=fminunc(@Rosenbrock,x0,options)

%[x,Q]=lsqnonlin(@Rosenbrock,x0)

[x,Q]=fminunc(@Rosenbrock,x0)

%[x,Q]=fminimax(@Rosenbrock,x0)

line(x(1),x(2),'Marker','.','MarkerSize',20); plot([x0(1),x(1)],[x0(2),x(2)],'k-'); colormap copper

function Q1=q(x) Q1=(x(1)-3)^2+(x(2)-3)^2+(x(3)-3)^2; function [f,g,H]=Rosenbrock(x) f=5*(x(2)-x(1)^2)^2+(1-x(1))^2;

if nargout>1 g=[-20*x(2)*x(1)+20*x(1)^3-2+2*x(1);10*x(2)-10*x(1)^2];

end

if nargout>2

H=[-20*x(2)+60*x(1)^2+2 -20*x(1);-20*x(1) 10];

end

ris38

Warning: Trust-region-reflective algorithm requires at least as many equations as

variables; using Levenberg-Marquardt algorithm instead. > In lsqncommon at 77

In lsqnonlin at 237 In ris38 at 5

Local minimum found.

Optimization completed because the size of the gradient is less than the default value of the function tolerance.

Рис. 3.8. Безусловная оптимизация в Matlab

45

<stopping criteria details>

x=

2.9993

2.9993

2.9993

Q1 = 2.5912e-012

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than twice the default value of the step size tolerance and constraints are

satisfied to within the default value of the constraint tolerance.

<stopping criteria details>

x=

3.0000

3.0000

3.0000

Q1 = 1.9232e-015

Warning: Gradient must be provided for trust-region algorithm; using line-search algorithm instead.

> In fminunc at 365 In ris38 at 9

Local minimum found.

Optimization completed because the size of the gradient is less than the default value of the function tolerance.

<stopping criteria details>

x = 3 3 3

Рис. 3.8. Продолжение

46

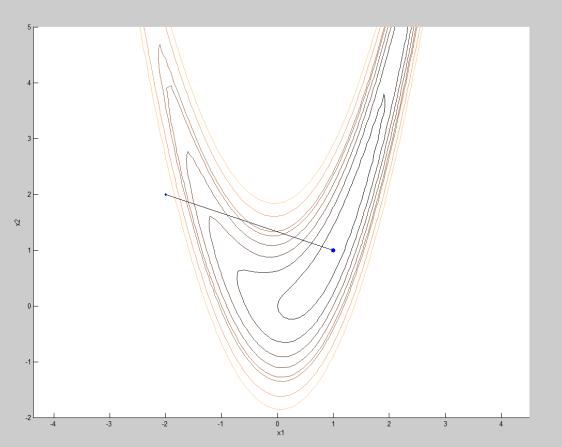
Q1 = 0

Warning: Gradient must be provided for trust-region algorithm; using line-search algorithm instead.

> In fminunc at 365 In ris38 at 29

Local minimum found.

Optimization completed because the size of the gradient is less than the default value of the function tolerance.

<stopping criteria details>

x=

1.0000

1.0000

Q = 2.0188e-012

Рис. 3.8. Окончание

47