Ис пользование функции minimize
x1 5	x2 5 - начальное приближение

			0		1
xm MinimizeQ( x1 x2)	xm	Q xm		xm
				0		1
xmax MaximizeQ( x1 x2)	xmax	Q xmax			xmax

*

Решение не получено, так как точкахточка ус тойчивого равновес ия (точка

минимакс а).

x1 5

x2 5

Given

d

Q(x1 x2)

0

d

Q(x1 x2)

0

- дополнительное ус ло вие

dx1

dx2

2

0

1

xm MinimizeQ( x1 x2)

xm

0

- решение найдено

Q xm

xm

3

x1 0

x2 0

Given

d

Q(x1 x2)

0

d

Q(x1 x2)

0

- дополнительное ус ло вие

dx1

dx2

2

0

1

12

xmax MaximizeQ( x1 x2)

xmax

1.8 10

- решение найдено

Q xmax xmax

3

Рис. 2.5. Окончание

	2.2. Метод множителей Лагранжа
Рассмотрим задачу оптимизации
	Q x extr,		(2.10)
	x X
где X x : x E n ,q x b .
Решим эту задачу методом множителей Лагранжа. Для этого [2]:
1)	введем вектор-строку множителей Лагранжа λ		...	m	.
Здесь m – число ограничений-равенств задачи;
2)	определим функцию Лагранжа как сумму целевой функции и ска-

лярного произведения вектора множителей Лагранжа и разности ограничений

L x,λ Q x λ b q x

(2.11)

или в развернутом виде

L x , x

,...,x

n

, ,

,...,

m

Q x , x

,...,x

n

m

b q

x , x

,...,x

n

;

i

i i

i

21

3) найдем стационарные точки функции Лагранжа (точки экстремума)

L x , λ					Q x			λ q x
x					x			x			(2.12)
L x λ			b q x
λ

Первые n соотношений (2.12) показывают, что градиент целевой функции должен равняться вектору множителей Лагранжа, умноженному на мат-

рицу Якоби для функций ограничений, т.е.

Q x

λ

q x

(2.13)

x

x

или в развернутом виде

x ,...,x

Q x ,...,x

m

q

n

i

n

, j

, ,...,n .

x j

j

x j

i

Остальные m условий представляют систему ограничений

q x

b .

Решая совместно m+n уравнений (2.12) получим значения m+n неиз-

вестных x

x

,...,x

и

λ

. Значения

x

дают локальное реше-

n

,...,

m

ние, т.е. являются решением задачи, если выполнены необходимые условия (2.12) и достаточные, которые состоят в том, что матрица Гессе

				L
				x
	L x , λ
				L
				x x
	x
		...
				L
				x	n	x

L		...		L
x x				x x
					n
L	...			L
							(2.14)
x				x xn
...	...			...
L			...	L
xn x
				xn

отрицательно определена или отрицательно полуопределена в точке локального максимума x , λ при том условии, что

q x dx .

x

Из (2.13) видно, что вектор градиента целевой функции Q x пред-

x

ставляет собой взвешенную сумму нормалей к кривым ограничений (или
градиентов к кривым ограничений	q x	), в качестве взвешивающих коэф-
	x

фициентов берутся неизвестные множители Лагранжа i .

22

Пример 2.1. Найти максимум функции Q x x x

при ограниче-

нии x x .

Поскольку

ограничение равенство

одно,

то m

и

вектор-строка

λ

.

Функция Лагранжа имеет вид

L x, λ x x

x x

.

Соответственно условия максимума (минимума) функции Лагранжа,

равно целевой функции

L x , λ

x

x

,

L x , λ

x

x

,

L x

, λ

x

x

.

	Решая систему уравнений находим x				, , x
								, , .
		, соответствующие решению задачи, измеряют
	Множители Лагранжа i
	чувствительность оптимального значения целевой функции Q x										к измене-
	ниям констант ограничений b	Q x				Q x*
	λ		, или	*i					,i	, ,...,m .	(2.15)
		b				bi
										равен нулю, то ма-
	Например, если какой-то множитель Лагранжа i

лые изменения соответствующей константы ограничений bi не окажут ника-

кого влияния на оптимальное значение целевой функции. В экономических задачах распределения ресурсов целевая функция имеет размерность стоимости, а ограничения устанавливают определенное значение количества ресурса (затрат и т.п.). Соответственно из (2.15) следует, что множитель Лагранжа имеет размерность цены.

Поэтому в экономических задачах множитель Лагранжа часто называют теневой ценой данного вида ресурса (затрат).

Рассмотрим примеры решения задач в Mathcad (рис. 2.6).

Поиск минимума с использованием функции find (классическая задача МП)

n 20	k 20	i 0 n	j 0 k
Q(x1 x2) 0.5 (x1 2)2 0.2(x2 3)2				q(x1 x2) x1	x2 1
x1i 0 0.2 i		x2j 0 0.2 j		Mi j Q x1ix2j	Zi j q x1ix2j

Рис. 2.6. Решение задачи методом множителей Лагранжа

23

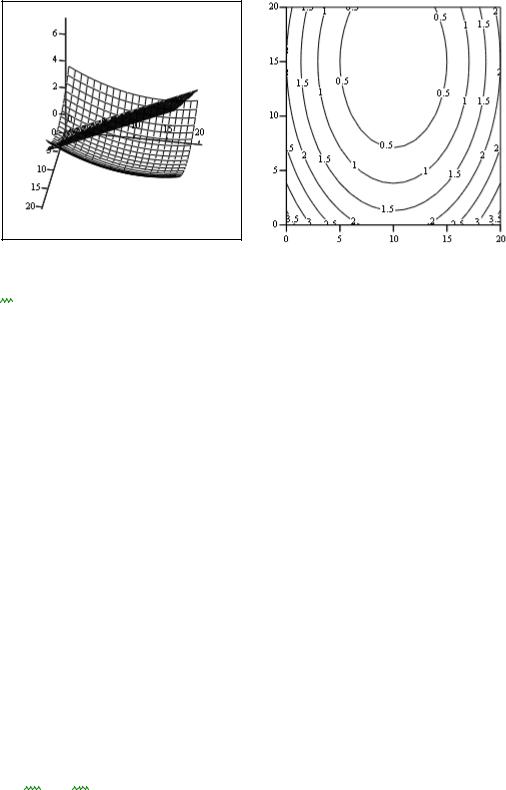
M Z	M
L(x1 x2 1 ) Q(x1 x2) 1 (1 x1 x2)	- функция Лагранжа

Необходимые ус ловия экс тремума (минимума или макс имума)

x1 0 x2 0 1 0

- начальное приближение

Given

d

d

d

L(x1 x2 1 )

0

L(x1 x2 1 )

0

L(x1 x2 1 )

0

d 1

dx1

dx2

x Find(x1 x2 1 )

xT (

0.857 0.143 1.143)

Q x0x1 2.286

L x

0x1x2 2.286

Дос таточные ус ловия

			d	2
						L(x1 x2 1 )
					2
MG		dx1
d			d				L(x1 x2 1 )

dx2 dx1

d d
							L(x1 x2 1 )
dx1 dx2
			d	2		L(x1 x2 1 )
		dx22

	x1	1		0
		G1				T	G1
	x2		0	0.4

		1		14
MG				1.469 10
			10 4
	3.189			0.4

x12 0.4 x22

Решение задачи с ис пользованием функции minimize

Вариант 1 (непос редс твенно)

x1 5 x2 5 - начальная точка поис ка

Рис. 2.6. Продолжение

24

Given

x1

x2

1

xm 0.857

xm MinimizeQ( x1 x2)

1

0.143

0

0

1

Q xm

xm

2.286

xm

xm

1

Вариант 2 (с ис пользованием функции Лагранжа)

x1 0

x2 0

1 0

- начальное приближение

Given

d

L(x1 x2 1 )

0

d

L(x1 x2 1 )

0

d

dx1

L(x1 x2 1 )

0

dx2

d 1

x MinimizeL( x1 x2 1 )

0.857

Q x0

x1 2.286

L x0x1x2 2.286

x

0.143

1.143

x0 x1 1

Рис. 2.6. Окончание

25