x0 MaximizeQ( x1 x2)

x0	0			0	1	70	0	1	1	8		0	2			1	2	1
	1		Q x0		x0		x0	x0				x0				x0

Рис. 3.4. Окончание

3.3.Методы решения задач нелинейного программирования

Хотя, условия Куна-Таккера (3.6) дают полную характеристику решения, но они не содержат конструктивного метода отыскания решения. Основными методами решения задач НЛП являются рекуррентные методы. Иногда их называют релаксационными, итеративными. Суть методов заключается в построении последовательности приближенных решений задачи, которая обладает следующими свойствами:

каждый последующий член последовательности x , x ,...,xk , где xk

–вектор х на к-ом шаге поиска, в определенном смысле предпочтительнее предыдущего, т.е. xk xk , где – знак предпочтения;

эта последовательность при больших k приближается к решению задачи x .

Рекуррентный процесс решения задачи можно представить как движение в n-мерном пространстве от точки к точке (рис. 3.5).

x

x

xk

x

xk

x

x

Х

x

x

Рис. 3.5. Иллюстрация итерационного процесса решения задачи НЛП

Наиболее распространенная форма организации процесса поиска

xk xk Гk рk ,k , ,...,

(3.8)

34

где xk - значение вектора х на k шаге поиска, рассчитывается; xk - значение вектора х на k-ом шаге поиска, уже реализованное;

Гk - матрица параметров рабочего шага на k -ом шаге поиска;

рk - вектор направления движения поиска, рассчитанный на k-ом шаге поис-

ка.

Выбор вектора рk определяет общую скорость сходимости процесса, а выбор элементов гk существенно влияет на количество вычислений на каж-

дом шаге.

Выражение (3.8) можно представить в виде xk xk xk ,

где xk - величина приращения вектора х или вектор-поправок на k-ом шаге

поиска.

Среди множества рекуррентных методов оптимизации можно выде-

лить:

градиентные методы и их модификации;

методы прямого поиска.

В градиентных методах поиска направление поиска на k-ом шаге

рk gradQ

Аэто значит, что целевая функция Q(x) задана аналитически и непре-

рывно дифференцируема.

Если есть проблема в аналитическом вычислении градиента, то прибегают к его оценке, например, методами планирования эксперимента в текущей точке xk .

Методы прямого поиска предполагают организацию процесса поиска непосредственно по соотношению значений целевой функции (вычисленных или измеренных) в заданных точках текущего плана эксперимента. Это ме-

тоды поисковой оптимизации.

3.4. Градиентные методы оптимизации

Рассмотрим задачу НЛП без ограничений

Q(x) min,	(3.9)
x X
где X x : x E n .
Для решения задачи (3.9) используем итерационный процесс (3.8)
xk xk Гk gradQ xk ,k , ,...,	(3.10)

35

			Q x	k
			x
где gradQ x					.
	k
			Q xk
			xn

Здесь знак «-» соответствует поиску минимума Q(x) , т.е. движение в

направлении, противоположном градиенту.

В зависимости от свойств матрицы параметров рабочего шага гk личают алгоритмы:

стационарные, когда Гk не зависит от k;

нестационарные, когда Гk зависит от k;

линейные, когда Гk не зависит от х;

нелинейные, когда Гk Г xk зависит от х.

Так для n	и линейной стационарной матрицы Г
		k

цедура (3.10) имеет вид

Q xk

Q xk

x

x

,

,k

,k

x

x

x

,k

x

,k

Q xk

Q xk

.

x

x

Отсюда следует взаимное влияние составляющих градиента.

Выбор значений элементов матрицы Гk

это непростая задача.

раз-

про-

Часто прибегают к диагональным матрицам, которые исключают взаимное влияние составляющих градиента

								k I ,
Гk				, Гk k
		nn				nn

где I – единичная матрица.

Рассмотрим процесс поиска на примере.

Пример 3.2.

Q(x)	x x x				x min .
						x E

Находим

36

												Q(x)
													x					x	x
																			x
							gardQ(x) Q(x)											x								.
													x
Выберем Г
		k	I .									.
Начальная точка поиска (стартовая точка) x
																										. В соответствии с
(3.10) для
1)	k
								x ,
					x								.													;
								x
									,
2)	k
					x			x ,																		.
													.													;
								x
									,																	.
3)	k
			x				x ,				.			. .								.
													.													.
							x							. .
								,			.														.

Как видно из расчетов, последовательность xk сходится к точке опти-

мума x

.

Выберем

Г

k

.

Повторим предыдущий расчет:

1)

k

x

;

2)

k

x

;

3)

k

x

.

Совершенно очевидно, что процесс поиска расходится, а потому оптимум не будет найден.

37

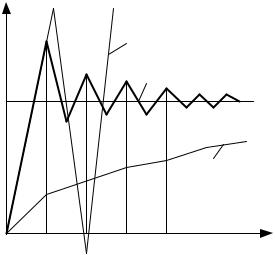
Влияние величины рабочего шага k					можно схематично представить
(рис. 3.5).
	xk		k
			k .
x
					k .
0	1	2	3		k
	Рис. 3.5. Влияние k			на процесс поиска

Как и при исследовании переходных процессов динамических систем от параметров системы (например, коэффициента усиления) процесс поиска может быть апериодическим, с перерегулированием и расходящимся.

Рассмотрим следующую процедуру выбора оптимального	на k-ом
k
шаге поиска:

1)задаем значение пробного шага h (одного и того же на всех итера-

циях);

2)определяем точку (вектор) y xk h gradQ xk ;

3)вычисляем Q(y) и Q xk ;

4)производим проверку неравенства gradQ xk T gradQ xk , (3.11)

где - произвольно выбранная константа (одна и та же при всех итерациях), а выражение в скобках есть скалярное произведение векторов градиента;

5) если неравенство (3.11) выполнится, то k h , иначе производим

дробление h (путем умножения на произвольное число ), до тех пор, пока не будет выполнено неравенство (3.11).

Алгоритм градиентного метода (метода наискорейшего спуска) [3]:

1) задать параметры задачи: n, Q(x) , начальную матрицу параметров

Q(x)

рабочего шага Г , вычислить вектор-функцию gradQ(x) ;

x

2) задать начальную точку поиска x , и итерации k ;

38

3)вычислить gradQ xk ;

4)найти значение k ;

5)положить xk xk k I gradQ xk ;

6)вычислить модуль градиента gradQ xk ;

7)если gradQ xk , то k k и переход к п. 3), иначе к п.8);

8)печать результатов: x xk , Q x , k.

Метод наискорейшего спуска (подъема) не пригоден для оптимизации сложных «овражных» функций, так как зацикливается не доходя до цели. Он обладает слабой способностью движения вдоль оврага (гребня) целевой функции.

Если неизвестно аналитическое выражение функции Q(x) , например,

она задана в виде формуляра расчета или алгоритма, либо вычисление производных функции Q(x) связано с трудностями, прибегают к вычислению

оценки градиента функции.

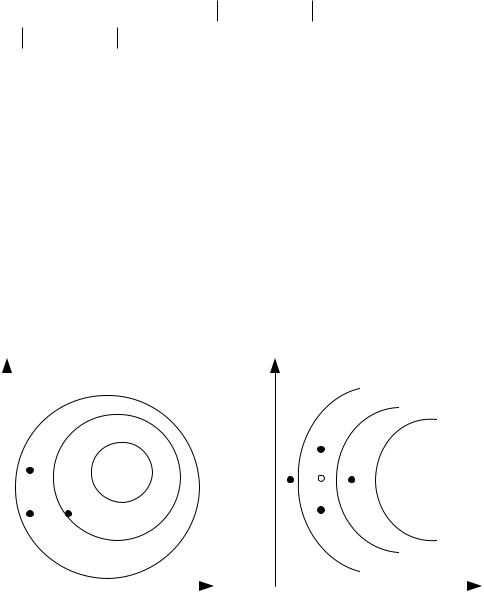
Для этого используют принцип линейной аппроксимации в текущей точке поиска. Реализуют либо план эксперимента центральной пробой, либо с парными пробными шагами (рис. 3.6).

x

x

xk ak e

xk ak e

xk ak e

xk

ak e

x k

xk ak e

x

k

a e

x k

k

x

x

а)

б)

Рис. 3.6. Планы эксперимента для оценки градиента: а) с центральной пробой, б) с парными пробами

Оценки градиента для плана с центральной пробой равны

					Q xk ak ei Q xk ,i , ,...,n	(3.12)
				ak

и для плана с парными пробами соответственно

39