3. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

3.1.Постановка задачи

Общая постановка задачи
Q x extr,							(3.1)
где X x : x En , x , q(x) b	x X
или в развернутом виде
Q x , x ,...,xn						extr	,
				x ,x ,..., xn X
при условии, что
q x , x ,...,xn b
q x , x ,...,xn b
...........................							(3.2)
qm x , x ,...,xn bm
x , x		,..., x	n		.

Здесь целевая функция Q(x) , или хотя бы одно из ограничений задачи qi (x) bi нелинейны относительно x.

Сделаем несколько замечаний относительно задачи нелинейного программирования (НЛП):

1)выбор знаков неравенств , совершенно условен. Например,

умножая неравенство x x на -1, можно превратить его в неравенство

x x , изменив тем самым знак неравенства на противоположный;

2)ограничение в форме равенств, например, x x , можно заменить ограничениями неравенствами x x и x x ;

3)условие неотрицательности переменных xi не является обязательным. Если некоторая переменная x не ограничена, то эту переменную

можно		заменить двумя переменными x'		и	x"	, полагая, что
x	x'	x"	, так что новая формулировка задачи не будет включать x					.

Таким образом, классическую задачу математического программирования (2.1) можно рассматривать как частную задачу НЛП, в которой условие неотрицательности переменных отсутствует и ограничения задачи в форме равенств.

Геометрически каждое из п условий неотрицательности x j , j , ,...,n

определяет полупространство неотрицательных значений независимых переменных, а пересечение всех таких полупространств представляет собой под-

27

X x En | g(x) b, x .

множество n-мерного евклидова пространства, называемое неотрицатель-

ным ортантом. Например, в E n неотрицательный ортант — это неотрицательный квадрант, т.е. первый квадрант плюс соответствующие полуоси. Каждое из т ограничений-неравенств

qi x , x ,...,xn bi ,i , ,...,m

также определяет множество точек в n-мерном евклидовом пространстве, а пересечение этих т множеств с неотрицательным ортантом составляет до-

пустимое множество

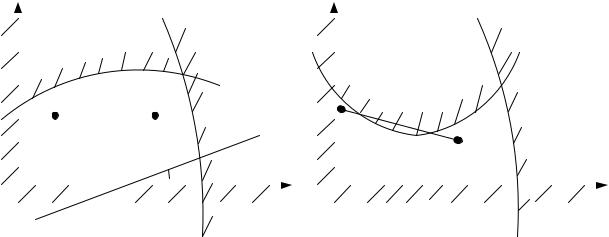
Важную роль в задачах НЛП играют выпуклости. Область Х является выпуклой, если отрезок прямой, соединяющей любые две точки области Х принадлежит этой области (рис. 3.1).

x

q (x) b

x

q (x) b

q (x) b

p

q (x) b

p

p

p

q (x) b

Х

Х

x

x

а)

б)

Рис. 3.1. Геометрическая интерпретация множества Х:

а) выпуклое; б) невыпуклое

Если область ограничений задана неравенствами

qi x bi , i ,...,m ,

где qi (x) – выпуклые функции, то эта область выпукла.

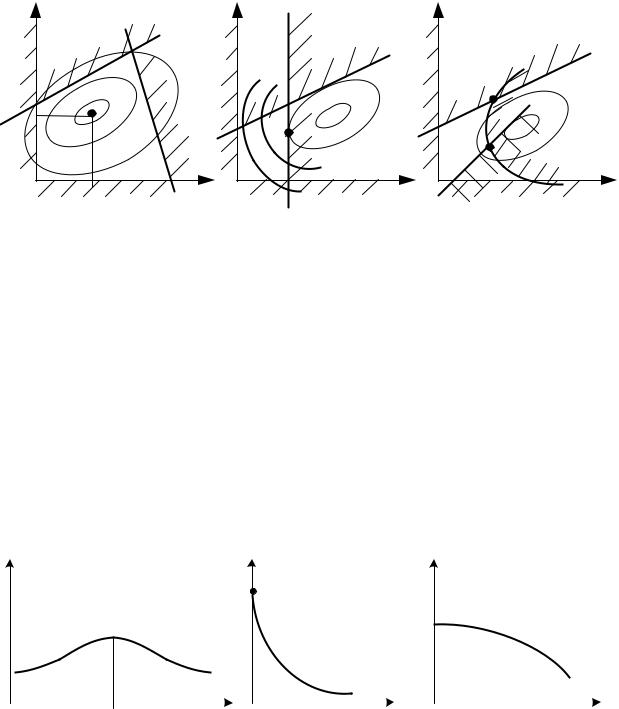
На рис. 3.2 проиллюстрированы решения задачи НЛП, когда точка экс-

тремума x является внутренней точкой множества Х (рис. 3.2 а), граничной точкой (рис. 3.2 б).

28

x		x	x
			А
x		x	Х
		Х
			Б
	x
		x	x
а)		б)	в)

Рис. 3.2. Решение задачи: а) внутри множества Х; б) на границе; в) два локальных экстремума А, Б

3.2.Условия Куна-Таккера

Рассмотрим частный случай задач НЛП вида
Q x max,	(3.3)

x X

X x : x E n , x .

Задачу (3.3) можно разбить на подзадачи, а именно: рассмотреть случай, когда x (рис. 3.3 а) и когда x (рис. 3.3. б, в).

Q(x)		Q Q x		Q	Q x
Q x
x		x			x

	x*	x	x		x
0			x*=0		x*=0
	а)		б)		в)

Рис. 3.3. Иллюстрация возможных решений задачи НЛП

В общем случае

29

Q x*	,если x*
x j	j
Q x*	,если x*
x j	j

j , ,...,n. (3.4)

Вводя дополнительные переменные в ограничения задачи (3.1), ее можно свести к классической задаче математического программирования (2.1) и воспользоваться методом множителей Лагранжа для ее решения.

Определим функцию Лагранжа в виде

L x,λ

Q x λ b q x .

(3.5)

Условия Куна-Таккера записываются следующим образом [2]

L x , λ

Q x

λ

q x

,

x

x

x

L x , λ

Q x

q x

λ

x

,

x

x

x

x

L x , λ

b q x ,

(3.6)

λ

λ L x , λ λ b q x

,

λ

x ,

λ .

Эти условия являются необходимыми и достаточными для существования (строго) локального максимума, если целевая функция (строго) вогнутая, а функции ограничений выпуклые, и если, при этом выполнено условие регулярности ограничений задачи, состоящее в том, что в некоторой точке допустимого множества Х все ограничения-неравенства выполняются как

строгие неравенства, т.е. если существует такой вектор			x , что	x и
q x b .
Как и в задаче классического математического программирования
множители Лагранжа задачи НЛП
	Q x	, i ,...,m ,		(3.7)
i	bi

и оценивают чувствительность оптимального значения целевой функции при изменении констант ограничений bi .

Пример 3.1.

30

Q x x

x

x x

x

x

max ,

x ,x X

x x

X

x x

x , x

.

Поскольку здесь целевая функция строго вогнутая (выпуклая вверх)

(т.к. минус стоит перед x

и x

),

а функции ограничений выпуклые, то сис-

тема неравенств, входящих в условия Куна-Таккера, имеет единственное ре-

шение в точке глобального максимума.

Функция Лагранжа имеет вид

x x ,

L x, λ x

x

x x

x x

x x

а условия Куна-Таккера

L

x

x

x

,

x

L

x

x

x

,

x

L

x

L

x

x x

x

x

x

x

x x x x ,

x , x .

L

x

x

L

x

x

L

L

x x

x x

, .

Хотя эти условия полностью характеризуют решение, тем не менее, они малопригодны для практического отыскания решений задачи.

Для решения примера 3.1 используем средства Mathcad.

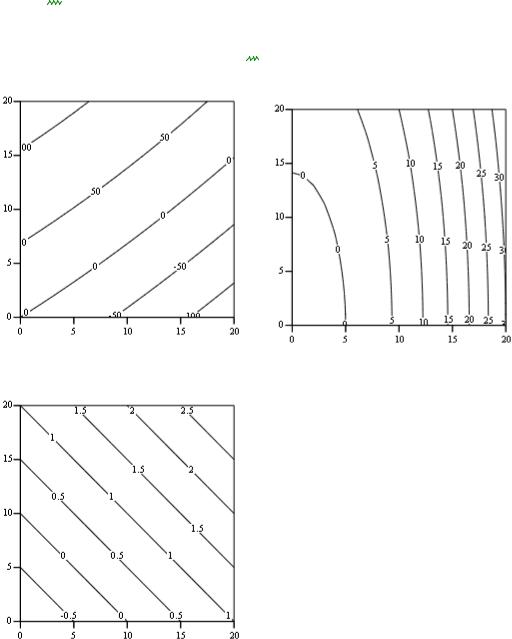
Как следует из результатов решения (рис. 3.4), точка экстремума x ( , ) лежит на границе допустимого множества Х. В этой точке

31

λ , ,			L x , λ		, ,	L x , λ	, ,	Q x ,
			x			λ
Q x
	, .
x
Решение задачи нелинейного программирования
Q(x1 x2) 8 x12			10x22 12x1 x2 50x1 80x2
q1(x1 x2) x1 x2 1				q2(x1 x2) 8x12 x22		2
n 20		m 20	i 0 n	j 0 m
x1i 0 0.1 i			x2j 0 0.1 j

M Q x1 x2 i j i j

Zi j q1 x1ix2j

Fi j q2 x1ix2j

M F

Z

Рис. 3.4. Решение задачи НЛП различными методами

32

С ис пользовани ем функции Лагранжа и ус ловий Куна-Т акера

L(x1 x2 1 2 ) Q(x1 x2) 1 (1 x1 x2) 2

2 8 x12 x22

Необходимые и дос таточные ус ловия экс тре мума

x1 1

x2 1

1 1

2 1

- начальное приближение (точка)

Given

d

d

L(x1 x2 1 2 ) 0

L(x1 x2 1 2 )

0

dx1

dx2

d

d

L(x1 x2 1 2 ) x1

L(x1 x2 1 2 )

x2

0

dx1

dx2

d

d

L(x1 x2 1 2 )

0

L(x1 x2 1 2 )

0

d 1

d 2

d

d

1

L(x1 x2 1 2 )

2

L(x1 x2 1 2 )

0

d 1

d 2

1 0

2 0

x1 0

x2 0

0

x Find(x1 x2 1 2 )

x

1

60

Q x0x1

L x0x1x2x3 70

70

0

V1(x1 x2)

d

Q(x1 x2)

12 x2

16 x1 50

V1 x0x1 38

dx1

V2(x1 x2)

d

Q(x1 x2)

12 x1

20 x2 80

V2 x0x1

60

dx2

V3(x1 x2 1 2 )

d

L(x1 x2 1 2 ) 12 x2 16 x1 1

16 2 x1 50

dx1

V3 x0x1x2x3 98

V4(x1 x2 1 2 )

d

L(x1 x2 1 2 )

12 x1 1

20 x2 2 2 x2 80

dx2

V4 x0x1x2x3

8.527

10 14

V5(x1 x2 1 2 )

d

L(x1 x2 1 2 )

1 x2 x1

V5 x 0 x 1 x 2 x 3

10 15

d 1

1.221

d

2

2

V6 x0x1x2

x3 1

V6(x1 x2 1 2 )

L(x1 x2 1 2 ) 2 x2

8 x1

d 2

В ис ходной пос тановке

x1 0

x2 0

- начальная точка поис ка

Given

x1 x2 1

8x12 x22

2

x1 0

x2 0

x0 MaximizeQ( x1 x2)

Рис. 3.4. Продолжение

33