2. КЛАССИЧЕСКАЯ ЗАДАЧА МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Общая постановка задачи
	Q x max,	(2.1)
	x X
	X x : x E n ,q x b .	(2.2)
Геометрически каждое из равенств, входящих в систему ограничений
qi x , x ,...,xn bi ,	i , ,...,m определяет множество точек в n-мерном евк-

лидовом пространстве, а пересечение всех m множеств представляет собой допустимое множество.

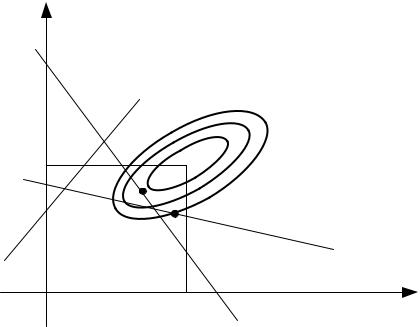
Ограничения типа равенств уменьшают размерность пространства поиска. На рис. 2.1 представлены линии равного уровня двумерной задачиn . Допустимое множество Х представляет собой плоскость прямоугольной системы координат. Если ввести одно ограничение q x b , то об-

ласть поиска решения задачи сужается до размерности ограничения – равенства.

	x
	q x b
			X
x
	A
	B		q x b
			x
	x		q x b
Рис. 2.1. Геометрическая иллюстрация задачи оптимизации

Точка экстремума x должна лежать на ограничении q x b (точка

А).

Если ввести еще одно ограничение q x b задача поиска экстремума

потеряет смысл. Решение задачи определено точкой В пересечения ограничений. Введение третьего ограничения не позволяет решить задачу (2.1).

16

Для решения задачи необходимо, чтобы n m. Разность n m называется числом степеней свободы задачи.

2.1. Задачи оптимизации при отсутствии ограничений

В случае отсутствия ограничений m необходимые условия экстремума – это равенство нулю градиента

											T
gradQ x Q x			Q x			Q x		... Q x
											. (2.3)
x				x		x		xn

Точка, в которой выполняется условие (2.3) называется стационарной точкой. Если функция Q x имеет в некоторой окрестности точки

x x ,...,xn непрерывные вторые частные производные и в этой точке вы-

полняются необходимые условия (2.3), то в случае, когда второй дифференциал

x T G x x ,

(2.4)

есть отрицательно определенная квадратичная форма, то x – точка строго локального максимума

Q x Q x x .

(2.5)

Это достаточные условия экстремума.

Если условие (2.4) строго положительно, то x – точка строго локаль-

ного минимума.

Здесь xT x x

... x

n

– произвольно малое приращение вектора x,

Q x

Q x

Q x

...

x

x x

x x

n

Q x

G x

Q x

Q x

Q x

...

– матрица Гессе.

x

x

x

x

x

x

x

j

n

i

Q x

...

...

Q x

x

n

x

x

n

(2.6)

Для интерпретации задачи оптимизации важное значение имеет выпуклость и вогнутость как целевой функции, так и ограничений задачи.

Функция Q x является выпуклой (выпуклой вниз) (рис. 2.2), если для

любых двух точек x и x выполняется условие
Q αx2 1 α x1 αQ x2 1 α Q x1 ,	(2.7)

при .

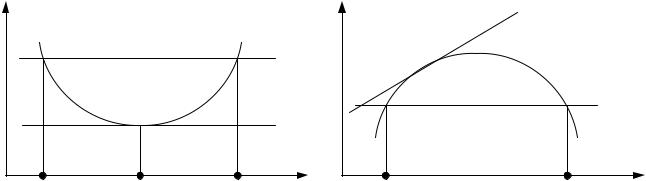
Выпуклые функции одной переменной (двух переменных) лежат выше любой касательной (плоскости) к данной функции (см. рис. 2.2).

17

Функция выпукла вниз,				если гессиан		2Q x
					G x	x x	положительно
						i	j
определен.
Q (x)					Q (x)
	αQ x2 1 α Q x1
				хорда			касательная
								хорда
				касательная
				x				x
x	α x	2	1 α Q x x		x			x
			1
Рис.2.2. Выпуклая вниз функция				Рис. 2.3. Выпуклая вверх (вогнутая)
						функция
Для выпуклых функций одной переменной это означает, что вторая
производная положительна, а для n-переменных положительно определена
квадратичная форма xT G x x .
Для выпуклой вверх (вогнутой) функции (рис. 2.3) справедливо соот-
ношение			Q αx2 1 α x1 αQ x2 1 α Q x1 ,
								(2.8)
при .
Такая функция лежит выше хорды, соединяющей любые две точки ее
графика. Соответственно гессиан вогнутой функции G x							отрицательно оп-
ределен.
Прямые, плоскости и гиперплоскости
			Q x a0x0 a1x1		a2x2 ... anxn ,			(2.9)
являются одновременно и выпуклыми и вогнутыми функциями и их гессиан
равен нулю.
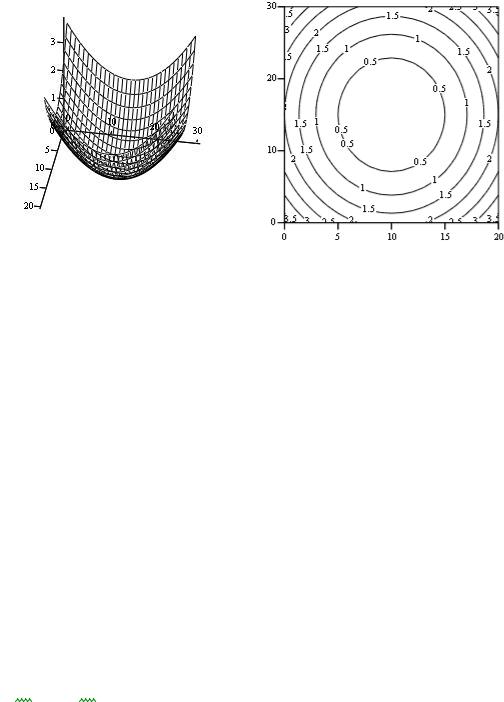
Примеры решения задач оптимизации в Mathcad (рис. 2.4, 2.5).

18

Поис к минимума с ис пользованием функции fi nd

n 20	k 30	i 0 n	j 0 k
Q(x1 x2) 0.5(x1 2)2 0.2(x2 3)2
x1i 0 0.2 i		x2j 0 0.2 j		Mi j Q x1ix2j

M

M

Необходимые ус ловия

x1 0

x2 0

- начальное приближение (начальная точка поис ка)

Given

d

d

2

Q x00x01 0

Q(x1 x2)

0

Q(x1 x2)

0

x0 Find(x1 x2)

x0

dx1

dx2

3

Дос таточные ус ловия

d2

d

d

Q(x1 x2)

Q(x1 x2)

dx12

dx1 dx2

14

MG

MG

1

1.469 10

d

d

d2

4

Q(x1 x2)

Q(x1 x2)

3.189 10

0.4

dx2 dx1

dx22

x1

1

0

M

T

M

x1

2

0.4 x2

2

x2

0

0.4

Квадратичная форма положительно определена для любого ?x и с ледовательно

	x0 - точка с трого глобального минимума.
	Поис к минимума с ис пользованием функции m inimize
	x1 0	x2 0 - начальное приближение
				2		0	1
	xmin MinimizeQ( x1 x2)		xmin					0
					Q xmin		xmin
				3

Рис. 2.4. Поиск экстремума с использованием функций find и minimize

19

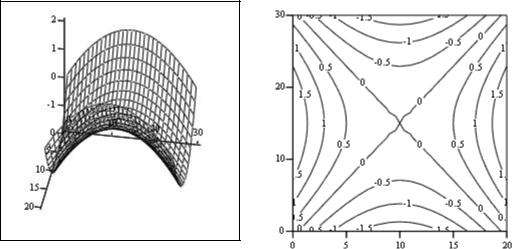
Нахождение экс тремума с ложной функции типа "с едло"

n 20

k 30

i 0 n

Q(x1 x2) 0.5 (x1 2)2 0.2 (x2 3)2

x1i 0 0.2 i

x2j 0 0.2 j

j 0 k

M Q x1 x2 i j i j

M

M

Необходимые ус ловия

x1 5

x2 5

- начальное приближение (начальная точка поис ка)

Given

d

Q(x1 x2)

0

d

Q(x1 x2)

0

dx1

dx2

2

0

1

xx Find(x1 x2)

xx

0

Q xx

xx

3

Дос таточные ус ловия

			d	2
						Q(x1 x2)
					2
MG		dx1
d			d				Q(x1 x2)
dx2 dx1

d d
							Q(x1 x2)
dx1 dx2
			d	2		Q(x1 x2)
		dx22

	x1	1		0
		M
			0	0.4
	x2

	1		0
MG		10 15
4.046			0.4

T M x12 0.4 x22

Квадратичная форма не удовлетворяет ус ловиям положительнос ти. В с едловой точке дос тигаетс я минимум по переменной х1 и макс имум по переменной х2.

Рис. 2.5. Нахождение экстремума сложной функции

20