9) если Qr Qs , то шаг признать неудачным, и точку xr следует сместить к центру x на половину расстояния между ними

xн		xri x i	,i ,...,n
ri

идалее перейти к п.6), пока не будет получена допустимая точка;

10)если Qr Qs , то шаг признается удачным

xsi xri , ,...,n, Qs Qr ;

11) проверить условие останова. Для этого вычислим оценку среднего квадратического отклонения целевой функции для текущего «комплекса»

			l
SQ			Q j Q ,
		l j

где Q l Q j ,

l j

и среднее квадратичное отклонение координат вершин текущего «комплекса»

Sx

n

Sxi ,

n i

l

Sxi

x ji xi

,

l j

xi

l

где

l

x ji ,i ,...,n .

j

Если S

Q

и S

x

, то останов процедуры, иначе переход к п.3).

Здесь и – достаточно малые константы, определяющие точность реше-

ния задачи.

Для невыпуклых функций и многоэкстремальных функций рекомендуется повторить процедуру поиска несколько раз. Так как точки «комплекса» формируются случайно, то имеется вероятность поиска глобального экстремума.

3.10. Методы случайного поиска

Методы случайного поиска являются прямым развитием известного метода проб и ошибок. Разработано достаточно много различных алгоритмов случайного поиска [3]. Основную идею методов рассмотрим на локальном случайном поиске с возвратом при неудачном шаге:

1) из исходного состояния делается шаг в случайном направлении

78

,n

где i – составляющие случайного вектора, например, равномерно распреде-

ленного в интервале [-1, 1];

xk xk k ;

2)определяется значение целевой функции Q xk ;

3)если Q xk Q xk , то при поиске максимума шаг признается удачным, точка xk считается новым исходным состоянием, и переход к п.

5), иначе к п. 4);

4) если шаг неудачный, то система возвращается в исходное состояние xk и переход к п. 1);

5) проверить условие останова (поиск максимума)

Q xk Q xk или k N .

Если хотя бы одно из условий выполняется, то останов процесса поиска, иначе k k и переход к п. 1).

Этот алгоритм можно записать в виде следующего рекуррентного выражения

x	k		k	удачный шаг,
xk				неудачный шаг.
xk

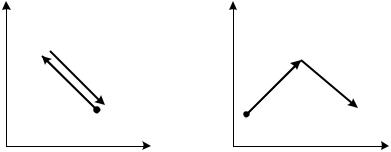
Геометрические представления поиска изображены на рис. 3.22.

x	x
xk	xk

x k	x	x k	x

а) неудачный шаг

б) удачный шаг

Рис. 3.22. Геометрия локального случайного поиска

Для генерации случайного вектора используют генератор случайных чисел вида rnd ( ) , который обеспечивает равномерное распределение

в интервале [-1, 1].

79

Предложенное правило останова на гладких, пологих функциях не всегда позволяет найти экстремум с заданной точностью. Так если xk и xk от-

личаются не значимо, в силу малости k k k k , то процесс поиска ос-

тановится, не доходя до экстремума.

С другой стороны, в области экстремума со свойствами острого пика, крутого гребня или оврага правило останова может не сработать, особенно при достаточно малом . В этом случае, процесс поиска при отсутствии ограничений на число шагов поиска может зациклиться. Потому желательно в процедурах поиска ввести ограничение на число шагов поиска.

Найденное решение xk можно использовать в качестве стартовой точ-

ки для более точных методов поиска экстремума. Учет ограничений задачи типа неравенств достигается возвратом:

x	k		k	- при удачном шаге;
xk				- при неудачном шаге или нарушении
xk
				ограничения типа неравенств.

Для повышения эффективности поиска прибегают к изменению величины рабочего шага k и изменению параметров распределения генератора

случайных чисел, к так называемой параметрической адаптации алгоритмов случайного поиска [3].

Величина рабочего шага k увеличивается при удачном шаге и умень-

шается при неудачном на тех же условиях, что и у ПСМ переменным шагом. Изменение параметров распределения связано со смещением центра

распределения случайной величины , например, в противоположную сторону от часто нарушаемых ограничений задачи.

Пример 3.4. Необходимо воспользоваться методом случайного поиска для решения следующей задачи

/

max ,

Q x , x x

x

X x : x E , x x

.

x X

и из точки x ,

Поиск реализовать из начальной точки x ,

без элементов адаптации. Результаты решения приведены на рис. 3.23.

Поис к макс имума

OR IGIN 1

F0 1

c 1

xx 5

xx 5

d 0.5

1

2

2

2 d

x

F0 c

x

xx

x

xx

F x

1

2

1

1

2

2

Рис. 3.23. Результаты решения примера 3.4

80

( k x Q )

k 1

xk

0

0

Q

F x

x

k

k

k

2

1

0.1

k k 1

xk xk 1

rnd(2) 1

rnd(2) 1

Q

F x

x

k

k

k

2

1

10 4

while

Qk

Qk 1

k k 1

xk xk 1

rnd(2) 1

rnd(2) 1

Q

F x

x

2

k

k

1

k

xk xk 1 if Qk Qk 1 ( k x Q )

k		663 i 1 k
x				x
i	1			i	2
		0				0
		-0.1			-0.061
		-0.1			-0.061
		-0.035			-0.127
	6.92·10-3				-0.166
	6.92·10-3				-0.166
		0.105			-0.242
		0.105			-0.242
		0.125			-0.309
		0.125			-0.309
		0.182			-0.305
		0.257			-0.213
		0.257			-0.213
		0.329			-0.158
		0.429			-0.135
		...				...
x		4.905		x		4.991
k		1			k	2

Рис. 3.23.

81

При поис ке минимума необходимо в логичес ком выражении изменить знак неравенс тва на противоположный.

Qi

-6.071

-6.185

-6.194

-6.186

-6.184

-6.292

-6.172

-6.235

-6.207

-6.28

-6.166

-6.048

-6.049

-5.958

-5.875

...

Qk 0.904

Продолжение