1.ВВЕДЕНИЕ В ЗАДАЧИ ОПТИМИЗАЦИИ

Встатических задачах оптимизации обычно не рассматриваются мето-

ды реализации принятого решения, т.е. определяется не величина и характер управляющего воздействия u t (закон управления), а непосредственно зна-

чение вектора состояния системы x, которое обеспечивает достижение цели управления.

Общая задача математического программирования состоит в поиске

(выборе) вектора х из допустимого множества X ,

обеспечивающего экстре-

мальное (максимальное или минимальное) значение целевой функции:

Q x extr,

(1.1)

где X x : x E n ,q x b ,

x X

q x и b – m-мерные вектор-столбцы,

q x , x ,...,xn

b

x

q

x , x

b

,...,x

x

x x

T ,

q x

n

, b

, x

...x

n

...................

...

...

q

x , x

,...,x

b

x

m

n

n

m

E n – n-мерное евклидово пространство (конечномерное действительное векторное пространство).

Функции ограничений q x ,...,qm x известны и непрерывно диффе-

ренцируемы. Вектор b – это вектор констант ограничений (заданные действительные числа).

Отметим, что максимизация Q x эквивалентна максимизации a сQ x при с , или минимизации a сQ X при с .

Введение дополнительного слагаемого а или положительного множителя с не изменяет задачи. Введением отрицательного множителя с можно преобразовать задачу максимизации в задачу минимизации (и наоборот). Хотя большинство стандартных процедур отдельно решают задачи максимизации и минимизации.

Эффективность решения задачи (1.1) определяется видом целевой функции Q x , видом ограничений задачи q x b и выбранным методом

решения задачи.

1.1.Функции одной переменной

Рассмотрим некоторые геометрические и практические аспекты решения задачи (1.1) для одной переменной.

Пример 1.1. Пусть целевая функция зависит от одной переменной и нет ограничений задачи.

5

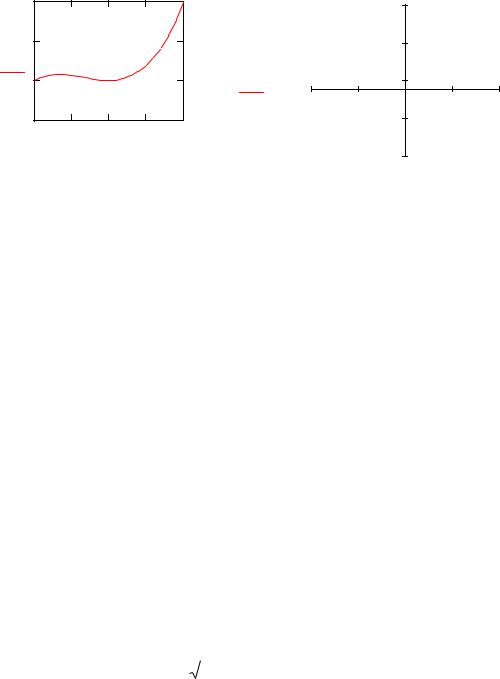
Построим плоский график функции в Mathcad (рис. 1.1) на интервалеa,b с шагом h и для случая, когда интервал аргумента не задан.

a 0	b 2		h 0.1
x a a h b			Q(x) x3	2x2	x 1	Q1(z) z3	2z2	z 1
3								1 103
2								550
Q(x)
1					Q1(z)			100
						10	5		0	5	10
00	0.5	1	1.5	2				350
		x						800
									z

а)

б)

Рис. 1.1. Решение примера 1.1: а) интервал задан; б) интервал не задан

Из графика видно, что функция Q x имеет точку локального минимума xmin и точку локального максимума xmax . . Знак приближенного

равенства свидетельствует о том, что мы воспользовались оценкой точек экстремума непосредственно с графика. Для детального исследования функции Q x интервал a,b можно расширить или изменить h . Первичное же пред-

ставление функции, когда интервал не задан (рис. 1.1, б) не отражает локальных экстремумов.

При аналитическом исследовании функции одной переменной необхо-

димым условием существования экстремума (максимума или минимума) не-
прерывной функции Q x является равенство нулю ее производной
Q x			.	(1.2)
x	Q x

Для примера 1.1 имеем

Q x x x .x

Это уравнение имеет два корня

x
									.
x								/

6

Определить какой из них максимум, а какой минимум можно только подстановкой в исходную функцию, либо провести исследование второй производной функции в точке экстремума

			Q x
			x			Q x x .
Имеем Q x		Q , т.е. положительна и, следовательно, это точка
минимума. Соответственно
			Q x		Q / , т.е. отрицательна, и это

точка максимума. Расчеты подтвердили очевидное из рис. 1.1.

Если Q x , то возникает неоднозначность. В этом случае можно воспользоваться следующим правилом:

- если функция Q x и ее производные непрерывны, то точка x являет-

ся точкой экстремума (максимума или минимума) тогда, и только тогда, когда n четное, где n-порядок первой необращающейся в нуль производной в

точке x ;

- если n-я производная Qn x , то точка x – точка максимума; - если n-я производная Qn x , то точка x – точка минимума.

Для поиска экстремума функции численными методами, реализованными в Mathcad, можно:

1)для непрерывной функции использовать равенство нулю производной от заданной функции (функция root);

2)для функции с переломами использовать функцию minerr. Для этого по графику выбирают число заведомо большее (или меньшее) экстремального значения функции и записывают его в качестве ограничения в блоке Given-minerr. Функция minerr возвращает значение аргумента, при котором расхождение между заданным числом и значением функции минимально. Возвращаемый результат зависит от выбора начального приближения (начальной точки поиска);

3)для непрерывных функций удобно использовать функции maximize и minimize. Ключевое слово Given можно опускать — оно необходимо лишь при наличии ограничений.

При анализе конкретного уравнения рекомендуется внимательно изучить график функции, на котором хорошо видны области нахождения экс-

тремумов. Построение графиков функции дано в разделе 3.6 части I. Определим экстремумы функции Q x примера 1.1 предложенными

методами (рис. 1.2) с учетом того, что мы построили и исследовали график функции (рис.1.1).

7

x 0

Ис пользование функции решения алгебраичес кого уравнения root (f(x),x)

Q(x) x3	2x2 x 1 - функция
x 2	- начальная точка пои с ка минимума

d

x0 root

Q(x)

x

x0

1

- экс тремум (минимум)

dx

d

2

Q(x0) 1

-значение функции в точке экс тремума

V(x)

Q(x) 6 x 4

2

V(x0) 2

dx

x 0

- начальная точка пои с ка макс имума

d

x1 root

Q(x) x

x1 0.333

- точка макс имума

dx

V(x1) 2

Q(x1) 1.148

-значение функции в точке макс имума

Ис пользование функции приближенного решения с ис темы уравнений minerr (x1,x2,...,xn)

x 2		- начальная точка пои с ка минимума
Given
Q(x)		0.9	- значение функции, заведомо меньшее чем в точке xmin
x2 Minerr(x)
x2 1				Q(x2) 1
x 0		- начальная точка пои с ка макс имума
Given			Q(x)			10
x3 Minerr(x)						x3 0.333	Q(x3) 1.148
Q(x) x3 2x2				x 1

Ис пользование функции minimize (Q,x1,...,xn) и maximize (Q,x1, ...,xn) - начальная точка пои с ка минимума

Given		x 1
xmin MinimizeQ( x) xmin 1				Q(xmin) 3
x2 2	- начальная точка пои с ка минимума
Given		x 0.5
xmn MinimizeQ( x) 1			xmn 1
x 2		- начальная точка пои с ка макс имума
Given		x 3
xmax MaximizeQ( x)			xmax 3	Q(xmax) 13
x 0	- начальная точка пои с ка макс имума

Рис. 1.2. Поиск экстремума стандартными функциями Mathcad

8

Given
xmm MaximizeQ( x) 0.333			xmm 0.333
x 2
Given	x 3
xm MaximizeQ( x) 3		xm 3
x 2
Given	x 0
xmm MaximizeQ( x) 0.333			xmm 0.333

Рис. 1.2. Окончание

Для непрерывных функций удобно использовать функции maximize и minimize. При этом оператор Given вводится только при наличии ограничений. Все рассмотренные методы требуют задания начальной точки поиска x0 . Вот почему важно иметь графическое представление функции.

Рассмотрим некоторые особенности поиска экстремума в условиях ограничений на переменную x в виде неравенства a x b . Данное неравенство выделяет некоторое допустимое множество Х, на котором необходимо исследовать функцию на экстремум. В этом случае точки экстремума могут лежать на границах допустимого множества Х. При этом первая производная в этих точках может быть не равна нулю. Поэтому использовать функцию root для поиска экстремума не следует.

Так, для примера 1.1 глобальный минимум функции Q(x) при x лежит на границе множества Х. При начальной точке поиска x (см. рис. 1.2), а глобальный максимум при ограничении x и начальной точке x лежит также на границе xmax .

Если множество Х не ограничено справа при поиске максимума из начальной точки поиска x , то решение не будет найдено, т.к. x

(множество не замкнуто).

Аналогично не будет найден и минимум функции, если множество не ограничено слева и начальная точка поиска x .

Если ограничение представлено строгим неравенством x , то максимум функции не существует, поскольку допустимое множество не замкнуто и xmax , но не может достичь ее границы в силу строгого неравенства.

Отметим, что применение процедуры maximize для данного условия выдает результат xmax . Итерационные методы осуществляют поиск с заданной

точностью, а поэтому выдают результат для этой точности.

В системе Matlab для поиска минимума на заданном интервале используется функция fminbnd. Обращение к функции

[х, Q]= fminbnd (@имя функции, xmin, xmax).

9

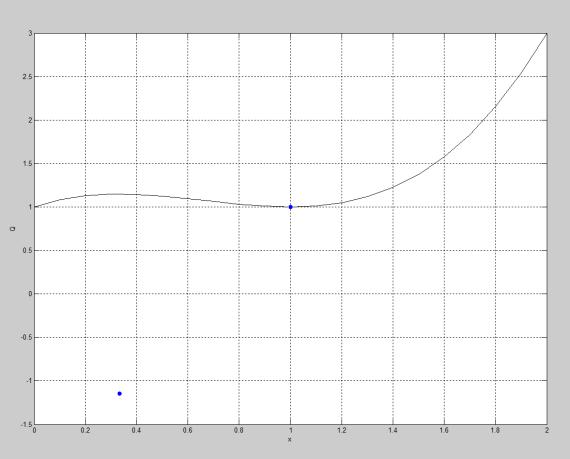
Для примера 1.1 результаты расчета представлены на рис.1.3.

Для поиска максимума функция Q(x) умножена на «-1». Первая точка вне графика отмечает xmax , Q xmax , вторая – xmin ,Q xmin .

%Одномерная отимизация function prog1.1

clear all x=0:0.1:2; y=f(x); plot(x,y,'k-'); hold on;grid;

xlabel('x'); ylabel('Q'); [x,Q1]=fminbnd(@f1,0,1) line(x,Q1,'Marker','.','Markersize',20); [x,Q]=fminbnd(@f,0.5,2) line(x,Q,'Marker','.','Markersize',20);

function Q=f(x) Q=x.^3-2*x.^2+x+1;

function Q1=f1(x) Q1=-1*(x.^3-2*x.^2+x+1);

Рис. 1.3. Решение примера 1.1 в Matlab

10