n
Q(δ) c j j extr,
j	δ

n
aij j bi , i ,...,m
j
	s n
p j k,
	j

где последнее ограничение может учитывать самые разнообразные условия. Если накладывается требование «должен», то в ограничении ставится

знак равенства: (число принятых вариантов «должно

быть» три).

Если требование «может», то — знак неравенства, в частности: - если накладывается требование «И», то

s

j ,

j

например, принятие и первого и третьего вариантов запишется ;

- если для вариантов накладывается требование «ИЛИ», то условие запишется

s

j .

j

Следовательно, если принять, что б соответствует «быть», нб — «не быть», то извечный вопрос «быть или не быть» запишется б нб .

5.4.Дискретное программирование

Взадачах дискретного программирования результатом решения должны быть целые, но не любые целые [4].

Пример 5.3. Мебельная фабрика выпускает диваны, кресла и стулья. Требуется определить, сколько можно изготовить спинок диванов, подлокотников кресел и ножек стульев при известном удельном расходе ресурсов (табл. 5.5), чтобы доход был максимальным.

126

Таблица 5.5

Условия примера 5.3

			Изделия		Наличие
	Показатели
		спинка	подлокотники	ножка	ресурса
		дивана	кресла	стула
	Цена, за единицу	20	6	8	-
	Древесина	10	5	3	206
	Трудозатраты	2	7	4	100
	Спрос	10	8	12	-
	План	x	x	x	bi

Причем выпуск спинок дивана может принимать любое значение, подлокотники изготавливаются парами, т.е. их количество должно быть кратно двум, а количество ножек стульев кратно четырем.

Решение. С учетом этих требований математическая модель задачи запишется:

Q(x) x x

x max,

x X

x x x ,

x

x

x

,

x ,

,

x

X

x ,

x

,

x ,

,

,

где k , k

— варианты количества подлокотников и ножек k ,...,ki .

Здесь

дополнительное

введение булевых

переменных дает возмож-

ность обеспечить выпуск изделий в кратном заданном количестве. Так, число подлокотников x может принимать следующие значения: если в результате

решения будет получено , а остальные , то x ; если , а остальные , то x и т.д.

Для решения задачи с учетом дополнительных условий мы ввели еще семь переменных и четыре ограничения. Следовательно, введение дополнительных требований привело к увеличению размерности задачи. Заметим, что

127

если бы нам требовалось определить выпуск спинок, подлокотников и ножек для одного изделия (комплекта), то можно было бы записать x x ;

x x и не вводить дополнительных ограничений и булевых переменных.

Но это была бы другая задача.

В результате решения задачи были получены следующие значения:

maxQ ;

x

;

x ;

x ;

;

.

При этом оказались не полностью использованы ресурсы: резерв по древесине равен 50, по трудозатратам — 4 ед.

Такое недоиспользование характерно для задач целочисленного программирования, т.е. ресурс остается, но на увеличение дискретного количества продукции его оказывается недостаточно

В общем виде задачу распределения ресурсов с учетом требования дискретного значения переменных можно записать:

n
Q(x) c j x j extr,
j		x X
n		bi , i	,...,m,
aij x j
j
	k j
X x j	dkj kj ,		j ,...,n,
	k
k j

kj ,

k

где d j , d j ,...,dkj ,...— дискретные значения, которые может принимать пере-

менная x j .

Для решения задач дискретного программирования применим метод ветвей и границ, метод сплошного перебора и метод фильтрующего ограничения [4].

Задача раскроя или задача рационального раскроя также относится к задачам дискретного программирования. Она заключается в выборе такого размещения заготовок в кусках материала, которое обеспечивает требуемую комплектность при минимальном расходе материала. В соответствии с особенностями технологии и организации раскроя различаются математические модели рационального раскроя для массового (серийного) и индивидуального (штучного) производства.

В массовом производстве при поступлении одинаковых кусков материала (например, бревна или листы стального проката одинакового размера), если можно перечислить все i , ,...,n доступные способы раскроя одного

128

куска материала на некоторые из j , ,...,m нужных видов заготовок, то за-

дача раскроя формулируется следующим образом: найти интенсивность применения (количество раз) xi каждого из раскроев, при которых

	n
	Q(x) xi min,
	i	x X
	n
x x : x E n , x , aij x j bj , j , ,...,m. ,
	i

где aij - количество j-х заготовок в i-м раскрое, b j - необходимое на одно из-

делие количество этих заготовок.

В условиях массового производства эта задача может быть решена как задача линейного программирования. При индивидуальном производстве (например, в судостроении, в штучном производстве крупных агрегатов) задача раскроя формулируется как задача целочисленного программирования.

Задача о рюкзаке. Пусть имеется n предметов, a j - вес, а c j - ценность j-го предмета, a j , с j . Требуется загрузить рюкзак, выдержи-

вающий вес b, набором предметов, суммарная ценность которых максимальна.

Введем булеву переменную x j , принимающую значение 1, если j-й предмет грузится в рюкзак, и 0 - в противном случае, j ,...,n . Задача имеет вид

n
Q(x) c j x j max,
j	x X
n	x j , ,
X a j x j b,		j ,...,n .
j

5.5.Задача коммивояжера

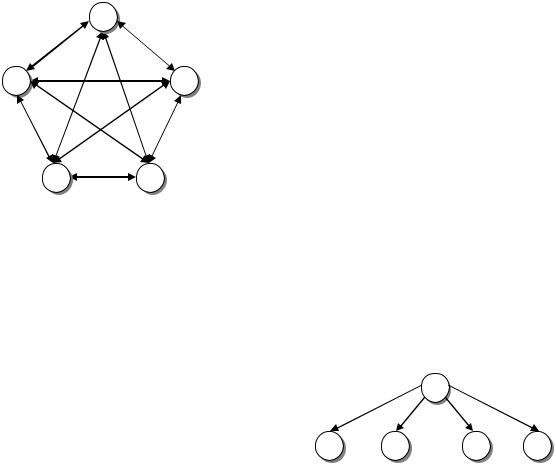
Пример 5.4 [4]. Пусть имеются пять пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт (рис. 5.6). Известно время перевозки из пункта i в пункт j (табл. 5.6).

Требуется найти такой маршрут, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда, чтобы его продолжительность была наименьшей.

Решение. Для решения этой задачи необходимо составить математическую модель. Введем обозначения: i и j — номера пунктов выезда и въезда; tij — время переезда из пункта i в пункт j. Из таблицы 5.6 видно, что tij в

общем случае может быть не равно времени переезда в обратном направле-

129

нии tij t ji (например, когда один пункт на вершине горы, а другой — у ее подножия). Введем булевы переменные:

,	если из пункта i торговец переедет в пункт j,
ij
,	если не поедет.
								Таблица 5.6
	1		Условия примера 5.4
		Из			В пункт j
		пункта
5	2
			1	2		3		4	5
		i
		1	0	10		25		25	10
		2	1	0		10		15	2
4	3	3	8	9		0		20	10
Рис. 5.6. Маршруты переезда		4	14	10		24		0	15
		5	10	8		25		27	0

Составим модель (рис. 5.7). Из п. 1 можно выехать в п. 2 или 5, или 3, или 4, или остаться в п. 1. Но при этом можно выехать только в одном единственном направлении. Это условие можно записать так:

,

или j ,

j

или для произвольного i-го пункта

ij , i ,..., .

j

	1
2	3	4	5

Рис. 5.7. Варианты переезда

Эти зависимости обеспечивают выполнение условия, что из каждого пункта выезд производится только один раз и только в одном направлении.

Условие въезда в п. 1 аналогично условию выезда из п. 1 (рис. 5.7). Требование минимальной продолжительности маршрута запишется в

виде целевой функции:

Q(δ) t t t t

t t t ... t min,

δ

130

где tij берутся из исходной таблицы 5.6, а ij - искомые переменные. Тогда всю задачу можно сформулировать:

Q(δ) tij ij min,
		i j		δ
ij , i ,..., ,
j
ij ,				j ,..., ,
i			; , i, j ,..., .
		ij

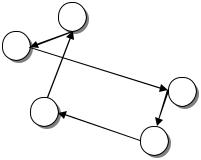
В результате решения задачи получим (рис. 5.8) следующие значения

					, остальные	;
					ij

min Q .

Переходя от частной к общей поставке, задачу коммивояжера можно сформулировать как:

n n
Q(δ) tij ij min,
i j	δ

n
ij , i ,...,n,
j
n
ij ,			j ,...,n,
i		; , i, j ,...,n.
	ij

1

10

5

8

14

2

4	10

20 3

Рис. 5.8. Оптимальный маршрут переезда

Попытаемся решить пример 5.4 непосредственно в Mathcad. Результа-

ты решения для ORIGIN=0 представлены на рис. 5.9.							Q x* . Это два не-
Полученное решение x*	x*	,	x*	x*	x*	,

связанных между собой контура.

Для получения гамильтонова контура, соответствующего обходу всех вершин графа, введем дополнительное ограничение x x , исключаю-

щее возврат из пятого пункта в исходный тотчас. Полученное решение (рис. 5.10) обеспечивает обход всех вершин графа.

131

n 4		i 0 n							j 0 n							xi j 0
110		10					25	25	10
	1	110					10	15	2
t	8	9					110	20	10
	14	10					24	110	15
10		8					25	27	110
				n			n
Q(x) ti jxi j
		i 0 j 0
Given
n							n							n						n							n
x							1 x					1 x							1 x
																									1	xi 4
	i	0						i 1						i 0		i 2						i 3								1
i 0							i 0													i 0						i 0
n								n									n					n
x0 j							1 x1 j						1				x2 j					1 x3 j					1		n
																												x4 j				1
j 0							j 0										j 0					j 0
																												j 0
x 0
x0 MinimizeQ( x)													0						1
															0	0	0
Q(x0) 60
													0		0	1	0		0
																					получили два нес вязанных контура
									x0 0						0	0	1		0
																					х15 =х51 ; х23 =х34 =х42
														0	1	0	0		0
													1		0	0	0		0

Рис. 5.9. Решение задачи коммивояжера

132

n 4		i 0 n							j 0 n					xi j	0
110		10					25	25	10
	1	110					10	15	2
t	8	9					110	20	10
	14	10					24	110	15
10		8					25	27	110
				n			n
Q(x) ti jxi j
		i 0 j 0
Given
n							n						n				n								n
x							1 x					1 x					x
																1							1	xi 4
i 0		i 0						i 1					i 0	i 2			i 0			i 3								1
							i 0																	i 0
n								n						n						n
x0 j							1 x1 j						1	x2 j						1 x3 j					1		n
																										x4 j				1
j 0							j 0							j 0						j 0

j 0

Вводим дополнительное ограничение, ис ключающее возврат тот час из 5 пункта в 1-ый

x 0	x0 4 x4 0			1
x0 MinimizeQ( x)				0					1
						0	0	0
					0	0	1	0	0
Q(x0) 62
		x0 0				0	0	1	0
					1	0	0	0	0
				0		1	0	0	0

Рис. 5.10. Решение задачи коммивояжера с дополнительным условием

133