x : x E , x ,i ,..., ,

i

x x x

x

x

X x x

x .

x x

x

x

x

x x x x x

Двойственная задача имеет вид

G λ max ,

λ

λ : λ E ,

i

,i ,..., ,

.

4.3.Методы решения задач линейного программирования

Если число переменных или число ограничений неравенств равно двум или трем, задачу возможно решить графически. Пусть

Q x cT x x			x		max ,						(4.12)
						x X
X x : x E , x											. (4.13)
	, x		, x			x		,	x x

Первым шагом решения задачи является введение вспомогательных переменных с целью превратить неравенства в равенства. Для неравенств вида вводят неотрицательные переменные xn i (либо yi )

ai x ai x ... ain xn xn i bi ,

и для неравенств вводят неотрицательные переменные xn i (либо yi )

со знаком минус

ai x ai x ... ain xn xn i bi ,

где i – номер строки в системе ограничений.

Введение новых переменных приводит к увеличению числа переменных, но не меняет существа задачи.

Для нашего примера имеем

	x x x ,	x , x		(4.14)
	X	x , x
	x x x ,
Число ограничений-равенств m , число неизвестных стало				n , а
именно:	x , x , x , x . Задача оптимизации имеет смысл, когда		n m . Оче-
	94

видно, если бы m n , то данная система имела бы единственное решение. Поскольку m n , то система имеет бесчисленное множество решений, т.е. имеется бесчисленное множество наборов переменных xi , удовлетворяющих

данным уравнениям-неравенствам. Если n m переменных положить равными нулю, то система m m может дать решение, при условии, что ее определитель . Если определитель равен нулю, то можно приравнять нулю другие n m переменных и т.д. Если решение получено, то оно называется базисным, а набор m-переменных при котором получено решение называется базисом, переменные – базисными. Остальные же n m переменные называются небазисными или свободными переменными. Для нашего примера имеем m базисных переменных и n m -свободных переменных. Выразим (4.14) через переменные x и x и представим на плоскости

x x x .		(4.15)
x x x
Полагая, что x , x находим	x x ,	x x ,

которые представим на плоскости (рис. 4.2). Для построения первой полуплоскости (прямой) полагая x , находим из (4.15) x (точка А), далее

полагаем x , находим из (4.15) x (точка В). Аналогично для второй полуплоскости: x находим из (4.15) x (точка С), x находим из

(4.15) x (точка D).

x

10

x 8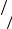

6	А
						направление
	С					градиента
4	Е
2
		В		D		x
	0
	2	4	6	8	x

Рис. 4.2. Графическое решение задачи ЛП

95

Выделение допустимого множества Х (4.13). Ограничениям - неравенствам x и x соответствует первый квадрант (штрихуем недопусти-

мое пространство слева от оси x и снизу от оси x ). Полагая в первом неравенстве (4.13) x , x находим , т.е. неравенство выполня-

ется и следовательно, точка 0 (начало координат) лежит в допустимом пространстве относительно полуплоскости x . Поэтому штрихуем недопус-

тимое полупространство справа от x .

Аналогично для второй полуплоскости x берем точку 0 ( x , x ) и получаем, что второе неравенство (4.13) выполняется, и, следовательно, недопустимое пространство лежит справа от полуплоскости x .

Таким образом, допустимое множество Х (4.13) – это выпуклый многогранник ОВЕС.

Далее для решения задачи нам необходимо найти вектор градиента целевой функции

		Q(x)
		x
	gradQ(x)					(4.16)
					.
		Q(x)
		x

Из (4.16) следует, что градиент целевой функции постоянен в любой точке множества Х. Для удобства рисования умножим составляющие градиента на константу, например, 3 и представим направление градиента на рис. 4.2. Линии равного уровня целевой функции (4.12) будут перпендикулярны направлению градиента. Поскольку задача на max, то мы должны двигаться в направлении градиента до граничной точки (вершины) или отрезка (грани) множества Х. Из графика видно, что граничной точкой множества Х будет точка Е. Все последующие линии равного уровня целевой функции будут за пределами допустимого множества Х. Для решения задачи минимизации необходимо двигаться в сторону антиградиента, т.е. в сторону уменьшения гра-

диента (4.16).

В вершине Е пересекаются две прямые x и x , т.е.

x x

xx .

Решая эту систему уравнений совместно находим x* , x* , Q x* .

Следует особо подчеркнуть, что при графическом решении задачи масштаб осей x и x должен быть одинаковым, т.е. сетка должна быть квад-

ратной (регулярной).

96

Для прямой задачи (4.12) сформулируем двойственную задачу

G λ					min ,			(4.17)
						λ
			,			,
				,				.

Решим прямую и двойственную задачу с использованием функций maximize и minimize (рис. 4.3).

Результаты (см. рис. 4.3) подтверждают теорему двойственности (4.8),
равенство Q x* , x* G *			, *	, а также выполнение теоремы о дополняющей

нежесткости (4.9).

Полученное решение позволяет оценить чувствительность оптимального решения прямой задачи к изменению констант ограничений задачи в соответствии с (4.10).

Так, например, если бы константа b в первом ограничении прямой задачи изменилась с 6 до 8, то оптимальное значение целевой функции изме-

нилось бы на Q *							b и новое оптимальное значение ста-
ло бы равным							.
Q(x1 x2) 3x1 2x2								- прямая задача
x1 0				x2 0			- начальная точка поис ка (начало координат)
Given			x1 0				x2 0		2x1 x2 6			x1 2x2 8
xmax MaximizeQ( x1 x2)										xmax	1.333				0	1	10.667
											3.333			Q xmax		xmax
G( 1 2 ) 6 1 8 2									- двойс твенная задача
1 0					2 0			- начальная точка
Given					1 0 2 0					2 1 2 3				1 2 2 2
min MinimizeG( 1 2 )										min			1.333		G min0		min1 10.667
													0.333
Проверка теоремы о дополняющей нежес ткос ти (4.9) для "ORIGIN=0"
				3			A	2	1		6
	C									b
				2				1	2		8
	CT minTA xmax 0													minT(b A xmax) 0

Рис. 4.3. Решение прямой и двойственной задачи ЛП

97

4.4.Идея симплекс-метода линейного программирования

Симплекс-метод линейного программирования позволяет решать задачи с числом ограничений до нескольких тысяч. Алгоритм симплекс-метода ЛП относится к итерационным алгоритмам, обеспечивающим последовательное движение к экстремуму целевой функции от вершины к вершине. Рассмотрим последовательность этапов алгоритма симплекс-метода на конкретном примере [4].

Пример 4.2. Четыре предприятия П , П , П , П выпускают продукцию в объемах x , x , x , x . Необходимо составить план производства с целью по-

лучения максимальной прибыли (табл.4.2).

Решение. Математическая модель задачи:

Q(x) x x x

x

max,

x X

x x x x ,

x

x x ,

x

X

x

x x

x

,

x , x

, x

, x

.

Таблица 4.2

Условия задачи

Ресурсы

Норма расхода ресурсов

Запас

П1

П2

П3

П4

ресурса

Трудовые

1

1

1

1

16

Сырье

6

5

4

3

110

Оборудование

4

6

10

13

100

Прибыль

60

70

120

130

-

План

x

x

x

x

-

В ограничения задачи введем дополнительные переменные y ,

y ,

y и

перепишем условие задачи в виде уравнений:

Q(x) x x x

x

max

x X

x x x x y ,

x

x x

y ,

x

X x

x

x

x

y

,

x

j

,

j ,..., ; y

i

, i ,..., .

98

Перепишем эти условия задачи в виде

Q(x) x x x x max,

x X

y x x x x ,

y

x

x

x

x

,

X y

x

x

x

x

,

x

j

, j ,..., ; y

i

, i ,..., .

Здесь y , y , y – базисные переменные в первом решении;

x , x , x , x –

свободные переменные в первом решении.

Последнюю постановку можно представить в виде первой таблицы симплекс-метода (табл. 4.3).

Правила составления симплекс-таблиц. Для первой таблицы:

1) в первый столбец записывают yi – базисные переменные, которые

находятся в уравнениях слева;

2) свободные переменные x j , заключенные в скобках, выносят в верхнюю строку таблицы;

3)в остальные столбцы записывают коэффициенты перед свободными переменными;

4)индексная строка есть результат вычитания из нуля коэффициентов перед свободными переменными целевой функции.

Для последующих таблиц (табл. 4.3, 4.4, 4.5, 4.6):

Таблица 4.3

Первая симплекс-таблица

	Базис	Свободные		Свободные переменные
		члены	x	x	x	x
	y	16	1	1	1	1
	y	110	6	5	4	3
	y	100	4	6	10	13
	Индексная строка	0	-60	-70	-120	-130

99

Таблица 4.4

Вторая симплекс-таблица

Базис	Свободные			Свободные переменные
	члены		x	x	x	x
y	108/13		9/13	7/13	3/13	0
y	1130/13		66/13	47/13	22/13	0
x	100/13		4/13	6/13	10/13	1
Индексная строка	1000		-20	-10	-20	0
						Таблица 4.5
			Третья симплекс-таблица
Базис	Свободные			Свободные переменные
	члены		x	x	x	x
y	12		1	7/9	1/3	0
y	26		0	-1/3	0	0
x	4		0	2/9	26/39	1
Индексная строка	1240		0	50/9	-40/3	0
						Таблица 4.6
		Последняя симплекс-таблица
Базис	Свободные			Свободные переменные
	члены		x	x	x	x
x	10		1	1/18	0	…
y	26		0	-1/3	0	…
x	6		0	13/6	1	…
Индексная строка	1320		0	70/9	0	…

1)выбираем наименьший отрицательный элемент в индексной строке при отыскании максимума, но наибольший положительный – при отыскании минимума, исключая вектор свободных членов;

2)этот элемент определяет ключевой вектор-столбец, и он вводится в

базис (столбец x выделен жирно в табл. 4.3);

3)компоненты вектора свободных членов делятся на положительные элементы ключевого столбца (16/1, 110/3, 100/13);

100

4)из полученных отношений выбирается наименьшее (100/13);

5)вектор-строка, содержащая наименьшее положительное частное, – ключевая и выводится из базиса (строка y выделена жирно в табл. 4.3);

6)на пересечении ключевых строк и столбца находится разрешающий элемент ( эр табл. 4.3);

7)преобразование матрицы:

7.1.Каждый элемент ключевой строки делится на разрешающий элемент (100/13, 4/13,6/13, 10/13, 13/13). Полученные частные являются элементами ключевой строки следующей таблицы (строка x табл. 4.4).

7.2.Ключевой столбец в новой таблице – нули, за исключением разрешающего элемента.

7.3.Остальные элементы новой таблицы рассчитываются по схеме:

Эн Эс Э Э , Эр

где Эн – новый элемент; Эс – старый элемент; Э – элемент ключевой строки; Э – элемент ключевого столбца; Эр – разрешающий элемент.

7.4. Если нулевая строка (столбец) содержит нуль, то соответствующий столбец (строка) в новой таблице не изменится.

Пункты 1-7 повторяются до тех пор, пока в индексной строке не останется ни одного отрицательного элемента при отыскании максимума (но ни одного положительного при отыскании минимума).

Из последней таблицы (4.6) видно, что:

1) в столбце свободных членов все элементы положительны, это значит, что полученное решение является допустимым;

2)в индексной строке все элементы также положительны. Это значит, что полученное решение — оптимально, т.е. максимизирует целевую функ-

цию. При этом оптимальным планом будут величины: x* , x* (значит, они базисные); x* x* (так как они свободные), целевая функция

Q x* .

Из этой таблицы также следует, что базисная переменная y* , а свободные переменные y* y* , т.е. в оптимальном плане резервы трудовых ресурсов и оборудования равны нулю, так как они используются полностью. А резерв ресурсов сырья y* , что свидетельствует о его излиш-

ках.

Проверим решение задачи с использованием функции maximize (это не симплекс-метод).

101

Q(x1 x2 x3 x4) 60x1				70x2	120x3 130x4
x1 0	x2 0		x3 0		x4 0 - начальная точка поис ка
Given
x1 x2 x3 x4 16
6x1 5x2		4x3	3x4 110
4x1 6x2		10x3 13x4 100
x1 0 x2		0	x3 0	x4 0

		10
x0 MaximizeQ( x1 x2 x3 x4)	x0		0	Q x00x01x02x03 1.32	3
			6		10
			0

Рис. 4.4. Решение примера 4.2

В системе Matlab используем функцию linprog, которая используется для решения задач линейного программирования вида

		Q(x) cТ x max ,			(4.18)
где X x : x En ,x				x X
	min	x x	max	, Ax b, A1x b1 .

Обращение к функции

[x, Q]= linprog(C, A, b, A1, b1, xmin, xmax).

В функции linprog по умолчанию используется прямо-двойственный алгоритм, который одновременно решает прямую и двойственную задачу.

Результаты решения двойственной задачи на печать не выводятся. Если в списке options входных параметров свойств итерационных алго-

ритмов, определить для Large Scale значение off, то будет использоваться симплекс-метод линейного программирования. Более подробно о списке options смотри [8].

Если исходная задача на максимум, то вектор «с» вводим со знаком минус. Если одно из неравенств, или более, определено как , то соответствующая строка матрицы А и элемент вектора b умножаются на «-1», что соответствует изменению знака неравенства.

Для примера 4.2 решение представлено на рис. 4.5.

%Пример 4.2

A=[1 1 1 1;6 5 4 3;4 6 10 13]; b=[16;110;100]; c=[60;70;120;130]; xmin=zeros(4,1); [x,Q]=linprog(-c,A,b,[],[],xmin)

Рис. 4.5. Решение примера 4.2 в Matlab

102

prim4.2

Optimization terminated. x = 10.0000

0.0000

6.0000

0.0000

Q = -1.3200e+003

Рис. 4.5. Окончание

Изложенные этапы симплекс-метода заложены в стандартных программах метода. Заметим, что если бы искать оптимальное решение путем перебора всех вершин, то например, для n , m число вершин множе-

ства Х равно . При скорости вычисления целевой функции в вершине

сек, просмотр всех вершин займет время T лет.

Аналогично, если проводить оптимизацию классическими методами с использованием множителей Лагранжа, получим количество решений, совпадающей с количеством вершин. В симплекс-методе число шагов, необходимое для поиска решения N , m , где m – число равенств (т.е. окончательный вид канонической формы).

103