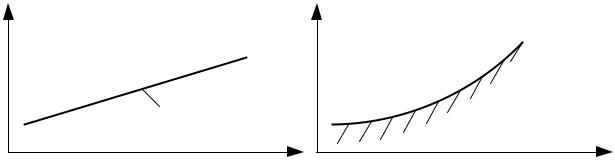
Представленная программа позволяет оценить эффективность методов оптимизации на достаточно гладких сепарабельных функциях и на овражной функции Розенброка, но с измененным множителем перед первым слагаемым (измените коэффициент на 100 и поэкспериментируйте с методами).

3.6.Учет ограничений в градиентных методах оптимизации

Мы уже ранее отмечали, что ограничения типа равенств уменьшают размерность исходного пространства, а ограничения типа неравенств выде-

ляют некоторую допустимую область в пространстве E n (рис. 3.9). Разработано много различных методов, учитывающих ограничения ти-

па равенств или неравенств или всѐ вместе. Например, метод возможных направлений, метод условного градиента, метод отсекающей гиперплоскости, метод линеаризации, методы проектирования с восстановлением связей, метод штрафных функций и др. Каждый из методов учитывает особенности задачи и наиболее эффективен при решении определенного класса задач.

x

q (x)

область решения

x

x

область решения

q (x)

x

Рис. 3.9. Области решения задач НЛП

Рассмотрим работу метода градиента при наличии ограничений неравенств (рис. 3.10а) [3].

Если имеется только ограничения типа неравенств, то при нарушении ограничений следует оптимизацию производить не по целевой функции, а по нарушенным ограничениям, то есть фактически вести оптимизацию функции

~	Q(x), при q j (x) 0,		j 1,2,...,s,
Q(x)		p
	qi (x), при qi (x) 0, p s,
		i 1

где р – число нарушенных ограничений.

Этот метод не эффективен, так как зацикливается не доходя до цели.

Поэтому чаще используют метод проецирования градиента [3].

48

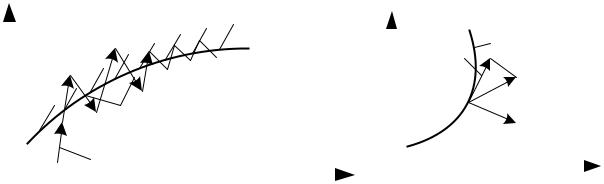
Смысл этого метода состоит в проецировании вектора градиента на ограничения и движении в направлении проекции градиента (антиградиента).

Определим сначала проекцию произвольного вектора p p ,...,pn на ограничение q(x) (рис. 3.10б).

		q(x)
Градиент ограничения			,...,	q(x)
	grad q(x)	x		xn	.

Очевидно, что проекция z вектора р на ограничение q(x) ортогональна градиенту ограничения и скалярное произведение z, grad q(x) . В

силу линейной зависимости
					z p grad q(x),				(3.18)
где		p, grad q(x) .
			grad q(x)
	x							x
								z	q(x)
			xk
									р
			движение по grad q(x)						gradq(x)
			xk
			движение по grad Q(x)			x			x
			а)						б)
			Рис. 3.10. Работа градиентного метода в условиях ограничений
					а) неравенств; б) равенств
	Тогда (3.18) перепишем в виде
					z p p,dir grad q(x) dir grad q(x) ,

где dir x			x			– знак направления.
			x

Рассмотрим далее проекцию вектора р на два ограничения q (x) и q (x) . Очевидно, что в этом случае процедуру проецирования следует произвести два раза, сначала получить z -проекцию р на первое ограниче-

ние, а затем z -проекцию z на второе ограничение:
z p p, dir grad q (x) dir grad q (x)

z z z , dir grad q (x) dir grad q (x) .

49

Подставляя первое уравнение во второе получим окончательное выражение для проекции вектора р на оба ограничения. Совершенно аналогично можно получить проекции произвольного вектора на любое число ограничений типа равенств.

Если нарушено ограничение типа неравенств, то движение будет аналогично, что и при нарушении ограничений типа равенств, вдоль поверхности q j (x) .

Совершенно очевидно, что за вектор р можно взять gradQ(x) , и тогда процесс поиска можно представить в виде

	~	xk xk k pk ,
		– проекция градиента целевой функции на ограничения,
	где pk gradQ(x)
	которые нарушены.
	Например, при нарушении i-го ограничения qi (x)		имеем
	~		нару-
	gradQ(x) gradQ(x) gradQ(x),dir grad qi (x) dir grad qi (x) , а при

шении j-го ограничения q j (x) имеем

~ . gradQ(x) gradQ(x) gradQ(x),dir grad q j (x) dir grad q j (x)

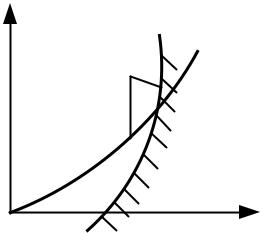
Метод штрафных функций является одним из наиболее простых и широко известных методов решения задачи математического программирования при ограничениях. Основная идея метода состоит в приближенном сведении задачи оптимизации при ограничениях к задаче оптимизации некоторой функции без ограничений. При этом эта функция выбирается так, чтобы она совпадала с искомой целевой функцией внутри допустимой области и быстро возрастала в задачах минимизации или спадала (максимизации) вне допустимой области (рис. 3.11).

Q

~	Q(x)
Q ( x )

q(x)

x

Рис. 3.11. Вид штрафной функции

Общий вид этой функции

50

~ ,

Q(x) Q(x) f q (x),...,qm (x) qm (x),...,qs (x)

где f и – неотрицательные функции штрафов за нарушение ограниче-

ний типа равенств и неравенств соответственно.

Конструкции f и могут быть самыми разнообразными. Например

~	m
Q(x) Q(x) ai qi (x) ,				(3.19)
~	i
	s
Q(x) Q(x) r			,	(3.20)
	j m q j (x)

где ai , r – коэффициенты штрафа.

Функции штрафа желательно выбирать такими, чтобы они резко воз-

растали при их нарушении и были малы в допустимой области Х. Правда,

~

при этом функция Q(x) вблизи ограничений содержит «гребни или овраги с

крутыми краями», что затрудняет работу градиентных методов.

~

Пример 3.3. Найти функцию Q(x) для следующей задачи

Q(x) x x x x min,

X x : x E , x , x

x X

, x ,

, x , x x x

, x

x

x

Воспользуемся функцией штрафа вида (3.20)

~

Q(x) Q(x) r

,

x x x

x

x x x

x

x

x

для r .

Здесь знак «+» для задач минимизации и «-» для задач максимизации. Целевая функция Q(x) не выпукла. Область ограничений тоже не явля-

ется выпуклой. Следует обратить внимание, что ограничение x , приве-

~

дено к виду x или x . Функция Q(x) овражная и для поиска

оптимума желательно запустить стандартную процедуру оптимизации для задач без ограничений с разных начальных точек. При этом коэффициенты штрафа для каждой новой итерации следует изменять по формуле

rl rl ,l , , ,...,

где l – номер новой итерации запуска процедуры с другой начальной точки. Для ограничений типа неравенств можно также использовать функцию

типа

	~		s
			bj	q j (x)	,
	Q(x) Q(x)
	51		j m

при q	j		(x) ,
где bj				(x) .
при q		j

Рассмотрим работу стандартных процедур Mathcad в условиях позиционных и функциональных ограничений задачи для функций, приведенных на рис. 3.7. Результаты решения для различных форм записи задачи представлены на рис. 3.12.

Стандартные процедуры успешно работают и в условиях ограничений задачи. Исключение представляют задачи с организацией цикла в блоке Given

(см. рис. 3.12).

Для ORIGIN=1
Q1(x1 x2 x3) (x1 3)2			(x2 3)2		(x3 3)2
g(x1 x2 x3) x1		x2 x3
x1 0	x2 0	x3 0		- начальная точка поис ка
Given
1 x1 1	0 x2 5				0 x3 3
g(x1 x2 x3) 10					1
x0 MaximizeQ1( x1 x2 x3)				x0			Q1 x01 x02 x03 4
					3
					3		g x0 x0 x0 7
							1	2	3
x-вектор
	1			3			0
n 3	a	1		xx 3			x 0		- начальная точка поис ка
		1		3			0
n		xxi	2			1
Q(x)
	ai xi			b		1	b1 10
i 1					1

	n	bixi
	g1(x)
	i 1
Given
1 x1 1	0 x2 5	0 x3 3	g1(x) b1

Рис. 3.12. Решение задач НЛП в условиях ограничений стандартными процедурами Mathcad

52

					1
xv MaximizeQ( x)			xv		3			Q(xv) 4								g1(xv) 7
					3
С ис пользованием штрафных функций
0.1
x	0.1 - начальная точка пои с ка
	0.1
F(x) Q(x) 1		1			1				1			1				1			1				1
									1 x							5 x							x
		10 g1(x)			x 1							x							x		3
					1			1			2				2			3					3
					1.398
xg MaximizeF( x)			xg		3.023			F(xg) 3.64							105			g1(xg) 7.421
					3											Q(xg) 2.565

Решение завис ит от начальной точки поис ка(попробуйте только не 0) и от коэффициента штрафа r. Т очное решение xx=(1,3,3)

С организацией цикла в блоке Given

	1				1
xmax	5		xmin		0
	3				0
Given
i 1 n			xmin x xmax
			i	i		i
xk MaximizeQ( x)				Процедура не работает

Рис. 3.12. Окончание

В системе Matlab условная минимизация решается методами безусловной минимизации, после сведения исходной задачи к функции Лагранжа или

штрафной функции.
Для линейных ограничений вида Ax b ,	A1x b1,	xmin x xmax и од-

ной двухкомпонентной нелинейной функцией ограничений вида [c, ceq]=nonlcon (x), для которой искомая точка минимума должна удовлетворять двум ограничениям c(x) 0, и ceq(x)=0, можно воспользоваться функцией

[x, Qval, e_flag, inform, lambda, grad, hes]=fmincon (@имя функции,

X0, A, b, A1, b1, xmin, xmax, @nonlcon, options).

Если какой-то из перечисленных входных параметров не используется, то вместо него задается пустой аргумент ([ ]).

Выходные параметры функции соответствуют:

53

х – решение задачи (точка минимума x* );

Qval – значение функции в точке x* ;

e_flag – признак успешного 1 (неуспешного -1) завершения поиска; inform – определяет число выполненных итераций (iteration), количест-

во обращений к функции (funcCount) и наименование использованного алго-

ритма (algoritm);

lambda – информация о множителях Лагранжа; grad – градиент функции в точке минимума x* ;

hes – матрица Гессе в точке минимума x* .

Для функции lsqnonlin возможны только позиционные ограничения

xmin x xmax .

Обращение к функции имеет вид

[x, Qval, e_flag, inform]= lsqnonlin(@имя функции, х0, xmin, xmax).

Обращение к функции fminimax мало чем отличается от вызова функ-

ции fmincon.

Рассмотрим работу стандартных процедур Matlab в условиях ограничений на примере функций, представленных на рис. 3.12.

%Условная оптимизация function prim3

clear all options=optimset('Display','final','GradObj','on'); x0=[0;0;0];

xmin=[-1;0;0]; xmax=[1;5;3]; [x,Q,Qmax,exitflag,inform]=fminimax(@Q1,x0,[],[],[],[],xmin,xmax,@gx,opti

ons)

function y=Q1(x) y=(x(1)-3)^2+(x(2)-3)^2+(x(3)-3)^2; function [c,ceq]=gx(x) c=x(1)+x(2)+x(3)-10;

ceq=[];

Qmax = 4.0000 exitflag = 4 inform =

iterations: 5 funcCount: 29

lssteplength: 1

stepsize: 9.9687e-009

algorithm: 'minimax SQP, Quasi-Newton, line_search' firstorderopt: []

constrviolation: 0 message: [1x767 char]

Рис. 3.13. Условная оптимизация в Matlab

54

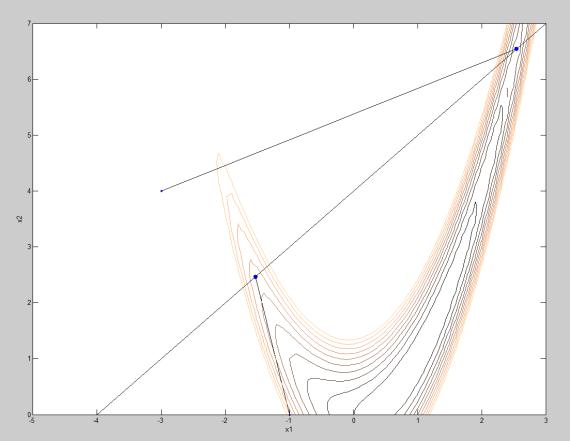
Рассмотрим работу процедуры fmincon при минимизации функции Ро-

зенброка и линейном ограничении	x1 x2 4 с представлением геометрии
поиска (рис. 3.14). В качестве	исходной точки возьмем x0 [ 3;4] и

x01 [ 1;0]. Точка x01 не удовлетворяет ограничениям задачи.

Для ускорения вычислительного процесса используем вычисление градиента и/или гессиана целевой функции.

%Условная оптимизация function rosus

clear all X0=-5:0.1:3;Y0=0:0.1:7; [X,Y]=meshgrid(X0,Y0); s=size(X);Z=zeros(s); for i=1:s(1)

for j=1:s(2) Z(i,j)=Rosenbrock([X(i,j);Y(i,j)]);

end

end V=1:10;

contour(X,Y,Z,V); grid off;hold on; x1=-5:5;x2=0:7;

xlabel('x1');ylabel('x2') plot([-4 3],[0 7],'k-'); x0=[-3;4];graf(x0) x0=[0;1]; graf(x0)

function graf(x0) A=[1 -1]; b=[-4];

options=optimset('Display','final','GradObj','on','Hessian','on');

%x0=[-3;4]; x0=[-1;0];

A=[1 -1];b=[-4]; line(x0(1),x0(2),'Marker','.','MarkerSize',10); [x,Q,e_flag,out,lambda,grad,hes]=fmincon(@Rosenbrock,x0,A,b)

%[x,Q]=fmincon(@Rosenbrock,x0,A,b)

line(x(1),x(2),'Marker','.','MarkerSize',20); plot([x0(1),x(1)],[x0(2),x(2)],'k-'); colormap copper

function [f,g,H]=Rosenbrock(x) f=5*(x(2)-x(1)^2)^2+(1-x(1))^2; if nargout>1

g=[-20*x(2)*x(1)+20*x(1)^3-2+2*x(1);10*x(2)-10*x(1)^2];

end

if nargout>2

H=[-20*x(2)+60*x(1)^2+2 -20*x(1);-20*x(1) 10];

end

Рис. 3.14. Минимизация функции Розенброка в условиях ограничений

55

rosus

Warning: The default trust-region-reflective algorithm does not solve problems with

the constraints you have specified. FMINCON will use the ac- tive-set algorithm instead.

For information on applicable algorithms, see Choosing the Algorithm in the

documentation.

>In fmincon at 486 In rosus>graf at 29 In rosus at 18

Local minimum possible. Constraints satisfied.

fmincon stopped because the predicted change in the objective function

is less than the default value of the function tolerance and constraints

are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>

Active inequalities (to within options.TolCon = 1e-006): lower upper ineqlin ineqnonlin

1

x=

-1.5312 2.4688

Q = 6.4841

e_flag = 5

out =

iterations: 10 funcCount: 31

lssteplength: 1

stepsize: 7.1415e-005

algorithm: 'medium-scale: SQP, Quasi-Newton, line-search' firstorderopt: 0.0042

constrviolation: 0 message: [1x776 char]

Рис. 3.14. Продолжение

56

lambda =

lower: [2x1 double] upper: [2x1 double] eqlin: [1x0 double] eqnonlin: [1x0 double]

ineqlin: 1.2483 ineqnonlin: [1x0 double]

grad = -1.2524 1.2441

hes =

93.5570 30.6164

30.6164 10.0300

Рис. 3.14. Окончание

57