11. Дискретное преобразование лапласа. Z – преобразование лорана

1) Решетчатые функции.

Н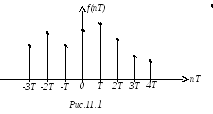аряду с функциями, определенным на всей вещественной прямойt, можно рассматривать функции, которые определены только в некоторых точках t₁, t₂,… Такие функции называют решетчатыми. Мы будем рассматривать функции, определенные только в равноотстоящих точках t=nT, где n – любое целое число, Т – постоянная, называемая периодом дискретности.(рис.11.1).

Эти функции принято обозначать f(nT).

Соответствующим подбором масштаба нетрудно положить Т=1 и рассматривать решетчатую функцию f(n), зависящую от целочисленного аргумента .

Для решетчатых функций вводятся понятия конечных разностей и сумм, которые в некотором смысле соответствуют понятиям производной и интеграла для обычных функций.

2) Конечные разности решетчатых функций.

Выражение

(11.1)

называется конечной разностью первого порядка решетчатой функции, или просто первой разностью.

Ясно, что - представляет собой решетчатую функцию, для которой может быть вычислена конечная разность. Т.о. первая разность от решетчатой функцииназывается разностью второго порядка решетчатой функции, или просто второй разностью

(11.2)

Разность к – го порядка решетчатой функции определяется формулой

(11.3)

Разность любого порядка можно выразить через значения решетчатой функции .

(11.4)

Аналогично для третьей разности:

(11.5)

Для разности произвольного порядка к справедлива формула

(11.6)

где . так называемые биноминальные коэффициенты, такие что:

.

Пример.

Формулы (11.1)-(11.6) позволяют выразить саму решетчатую функцию через её разности различных порядков.

Из (11.1)

(11.7)

Из (11.2)

откуда

. (11.8)

Используя равенство (11.3) при к=3 и равенства (11.4), (11.7), (11.8) получим

(11.9)

Продолжая вычисления можно получить общую формулу

, (11.10)

при n=0

(11.11)

Формулы (11.10) и (11.11) выражают значения решетчатой функции через её конечные разности до порядка l включительно. Эти формулы являются дискретным аналогом разложения непрерывных функций в ряд Тейлора.

Примеры.

1).,

.

2)..

3).

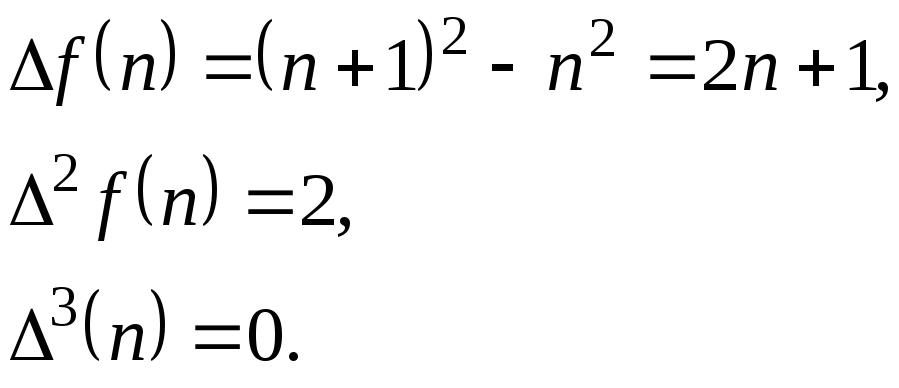
4).

Отметим, что операция взятия конечных разностей является линейной операцией, что следует из определения конечной разности

.

Используя выражение (11.1), можно вывести формулу для вычисления разности произведений 2-х функций

.

3) Суммирование решетчатых функций.

Рассмотрим теперь операцию, которая является обратной по отношению к операции взятия конечной разности. Пусть решетчатая функцияопределена при положительных значениях аргументаn=0,1,2… Требуется найти такую решетчатую функцию F(n), для которой функция является первой разностью.

Эта задача аналогична задаче о нахождении первообразной в анализе обычных функций.

Искомая функция имеет вид

.

Действительно,

Функцию F(n) называют первообразной для решетчатой функции .

Если F(n) является первообразной для , то и функцияF(n)+С так же является первообразной для .

Если решетчатая функция определена при всех целочисленных значениях аргумента, то для определения первообразной необходимо дополнительно потребовать, чтобы при каждом конечномn сходился ряд

.

При этом условии первообразная определяется выражением

.

И общий вид первообразной для данной решетчатой функции определяется формулой

.

Значение постоянной С можно выразить через значение первообразной при некотором фиксированном значении аргумента n=N.

.

Откуда,

.

для любого n>N.

Эта формула является аналогом формулы Ньютона – Лейбница, а выражение стоящее справа иногда называют определенной суммой.

Эту формулу можно преобразовать:

Учитывая, что можно записать и так.

, а

при N=0 получим

.

Пример. Для найти сумму F(n).

по формуле суммы членов геометрической прогрессии.