- •Введение
- •1. Понятие оригинала
- •2. Изображение по лапласу
- •3. Изображения простейших элементарных функций
- •4.Свойства преобразования лапласа
- •2С) Теорема подобия
- •3C) Теорема затухания (Теорема смещения)
- •5C) Теорема опережения.
- •10С) Интегрирование изображений.
- •11С) Теорема умножения изображений (теорема Бореля)
- •12С) Умножение оригиналов.
- •5.Примеры нахождения изображений с помощью таблиц 1 и 2
- •6. Импульсные функции и их изображения
- •7.Формула обращения преобразования лапласа
- •1)Тождественные преобразования и применение таблиц 1 и 2.
- •2) Вычисление оригиналов с помощью вычетов.
- •8.Применение преобразования лапласа для решения уравнений и систем
- •8.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.2 Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.
- •8.3 Решение дифференциальных уравнений с переменными коэффициентами.
- •8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.5 Линейные дифференциальные уравнения с запаздывающим аргументом.
- •8.6 Интегральные уравнения типа «свертки».
- •8.7 Линейные интегро-дифференциальные уравнения.
- •9.Решение диференциальных уравнений в частных производных и задач математической физики
- •10. Применение операторных методов для анализа линейных систем
- •11. Дискретное преобразование лапласа. Z – преобразование лорана
- •1) Решетчатые функции.
- •2) Конечные разности решетчатых функций.
- •3) Суммирование решетчатых функций.
- •4) Определение дискретного преобразования Лапласа.
- •5) Формула обращения.
- •1С) Теорема линейности.
- •Библиографический список
- •Оглавление
10С) Интегрирование изображений.
Если
![]() сходится, то
сходится, то
![]() .
.
Интегрирование
изображения в пределах от р
до
![]() соответствует делению оригинала наt.
соответствует делению оригинала наt.
Доказательство:
![]()
![]()

Этот
интеграл – есть изображение по Лапласу
функции
![]() .
.
Пример.
Найти изображение функции
![]() .
.
Решение:
![]() ,
тогда
,
тогда
![]()
11С) Теорема умножения изображений (теорема Бореля)
Рассмотрим некоторые понятия:
сверткой двух функций f(t) и g(t) называется интеграл
![]() .
.
Этот интеграл является функцией переменной t.
Свертка коммутативна f*g=g*f.
Если f и g – оригиналы, то и f*g тоже оригинал.
Операции свертки оригиналов соответствует произведение изображений.
![]() .
.
Это и есть теорема умножения изображений Бореля.
Доказательство:
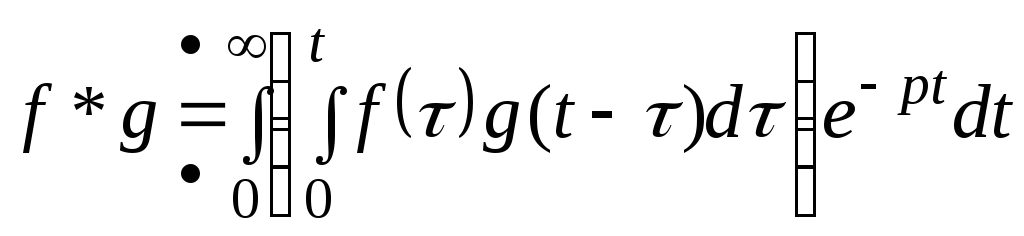 .
.
Р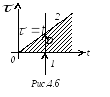 ассмотрим
это выражение как двойной интеграл по
бесконечной областиD
(рис.4.6).
ассмотрим
это выражение как двойной интеграл по
бесконечной областиD
(рис.4.6).
Пределы интегрирования:
по
![]() от
от
![]() до
до
![]() ;
;
по
t
от 0 до
![]() .
.
Изменим порядок интегрирования

![]() ч.т.д.
ч.т.д.
Рассмотрим специальный случай теоремы умножения. Найдем оригинал изображения pF(p)G(p)
![]() ,
тогда по теореме Бореля
,
тогда по теореме Бореля

Эта формула носит название интеграл Дюамеля.
12С) Умножение оригиналов.
Подобно тому, как произведению изображений соответствует свертка оригиналов, так и умножению оригиналов соответствует свертка изображений в комплексной плоскости.
![]()
Выражение справа - свертка изображений.
П
![]()
![]()
![]()
![]()
 уть
интегрирования (
уть
интегрирования (![]() )
показан на рис.4.7.
)
показан на рис.4.7.
Полученные результаты занесем в таблицу 2., которой удобно пользоваться при решении примеров и задач.
Таблица2.
|
|
|
|
1.линейность:
|
|
|
2.Теорема подобия
|
|
|
3.Теорема смещения
|
|
|
4.Теорема запаздывания
|
|
|
5.Теорема опережения
|
|
|
6.Предельные соотношения для изображения
|
|
|
7.Диффенцирование оригинала
…
|
…
|
|
8.Дифференцирование изображения
…
|
…
|
|
9.Интегрирование оригинала
…
|
…
|
|
10.Интегрирование изображения
|
|
|
11.Умножение изображений (теорема Бореля)
|
|
|
12.Интеграл Дюамеля
|
|
5.Примеры нахождения изображений с помощью таблиц 1 и 2
1).Найти
изображение для оригинала
![]() .
.
Решение.
![]() .
.
2).Найти
изображение для оригинала
![]() .
.
Решение.
![]()
3).Найти
изображение для оригинала
![]()
Решение.
![]()
4).Найти
изображение для оригинала
![]() .
.
Решение.
Так
как
![]() (теорема смещения), то
(теорема смещения), то
![]() и
и
![]() .
.
5).Найти
изображение для оригинала
![]() .
.
Решение.
Так
как
![]() ,
то
,
то

6).Найти
изображение для оригинала
![]() .
.
Решение.
Учитывая,
что
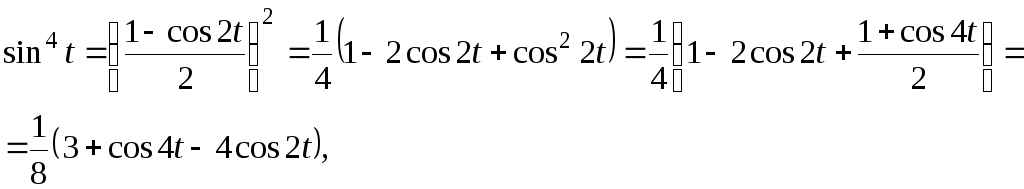 получаем:
получаем:
![]() .
.
7).Найти
изображение для оригинала
![]() .
.
Решение.
Так
как
![]() ,
то
,
то
![]() ;
;
но
если бы
![]() ,
то по теореме запаздывания:
,
то по теореме запаздывания:
![]() ,
получили бы
,
получили бы
![]() .
.
8).Найти
изображение для оригинала
![]() .
.
Решение.
Так
как по умолчанию
![]() ,
то преобразуем
,
то преобразуем
![]() ,
тогда.
,
тогда.
![]() .
.
9).Найти
изображение для оригинала
![]() .
.
Решение.
По теореме запаздывания будем иметь:
![]()
10)
Найти изображение для оригинала
![]() .
.
Решение.
Применяя теоремы запаздывания и смещения, получим
![]()
11)
Найти изображение для оригинала
![]() .
.
Решение.
Применяя теорему дифференцирования изображения:
![]() имеем
в данном случае:
имеем
в данном случае:
![]() потому
потому
![]()
12)Найти
изображение для оригинала
![]() .
.
Решение.
Применяя
теорему смещения:![]() и используя результат примера 11, получим
и используя результат примера 11, получим
![]()
13)Найти
изображение для оригинала
![]() .
.
Решение.
Применяя теорему интегрирования изображения:
![]() ,
имеем в данном случае:
,
имеем в данном случае:
![]() тогда
тогда
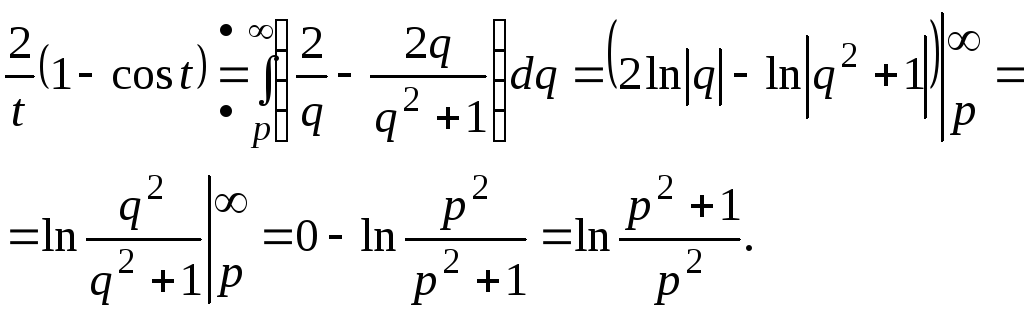
14)Найти
изображение для оригинала
![]() .
.
Решение.
На основе свойства интегрирования оригинала:
![]() имеем
в данном случае:
имеем
в данном случае:
![]() .
Для нахождения
.
Для нахождения
![]() применим теорему интегрирования
изображения:
применим теорему интегрирования
изображения:
![]() в
данном примере
в
данном примере
![]() поэтому
поэтому

Тогда
![]()