6. Импульсные функции и их изображения

Функции, которые не стремятся к нулю при, можно считать изображениями лишь в совершенно условном смысле. Эти условные изображения и соответствующие им оригиналы, так называемые импульсные функции, были введены Дираком и оказались полезными в ряде прикладных задач, в которых приходиться иметь дело с величинами, имеющими характер мгновенного толчка.

Рассмотрим функцию , график которой приведен на рис.6.1.

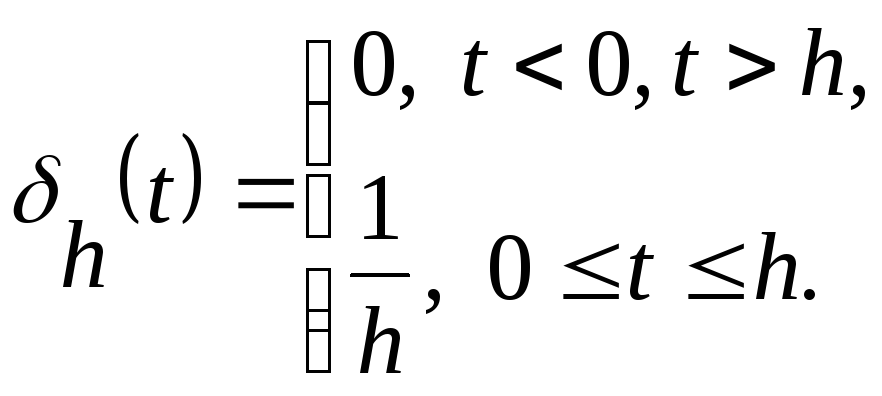
Она представляет величину, которая действует лишь на отрезке , где имеет постоянное значение, суммарный эффект ее действия равен.

1

Рис.6.1

Предположим теперь, что ; семейство функций, очевидно при этом расходится, но мы введем условную функцию, которую будем считать пределом такого семейства,

,

и называть импульсной функцией нулевого порядка, или короче,- функцией. Импульсная функцияравна нулю всюду, кроме точки, где она равнаи, тем не менее, для нее считается справедливым соотношение

,

предельное для такого же соотношения с функцией .

Таким образом, - функция представляет собой условное сокращенное образование для вполне определенного предельного процесса, который часто рассматривается в физике: бесконечно большая величина, действующая в бесконечно малый промежуток времени с суммарным эффектом, равным 1. Введение этой функции сильно упрощает вычисления, связанные с таким предельным процессом. Дельта – функция относится к обобщенным функциям.

Условимся считать, что изображение - функции получается как предельное для изображения функции:

, которое

по теореме запаздывания равно

Переходя к пределу при , получим (условно)

Полученный результат можно «подкрепить» следующими соображениями.

На рис.6.1 изображены пунктиром график интеграла функции

.

Из этого графика видно, что пристремится к функции, так что положим. Но тогда, а так как, то по теореме дифференцирования оригиналов снова получаемЗначение оригинала при, участвующие в этой теореме, считаем равным нулю на том «основании», что оно получается как предельное прииз значений; формальное применение указанной теоремы, где мы должны положить, привело бы к неправильному результату. Удивляться этому не следует, ибо мы применяем теорему в ситуации, когда ее условия нарушаются.

Для любой функции-оригинала по теореме о среднем получаем:

,

где . Переходя здесь к пределу при, считаем по определению

а если разрывна при, тообозначает ее правое предельное значение.

В соответствии с этим снова получаем

Аналогично вводятся импульсные функции высших порядков:

- дельта-функция первого порядка,

- дельта-функция второго порядка,

и т.д.

7.Формула обращения преобразования лапласа

Из математического анализа известно экспоненциальное преобразование Фурье абсолютно интегрируемой функции :

и формула его обращения:

- интеграл понимается в смысле главного значения.

Пусть - функция-оригинал. Тогдапри будет абсолютно интегрируемой и ее можно преобразовать по Фурье:

- преобразование по Лапласу для функции

Таким образом, получили: преобразование по Фурье есть преобразование по Лапласу функции.

Тогда из формулы обращения преобразования Фурье получаем:

или

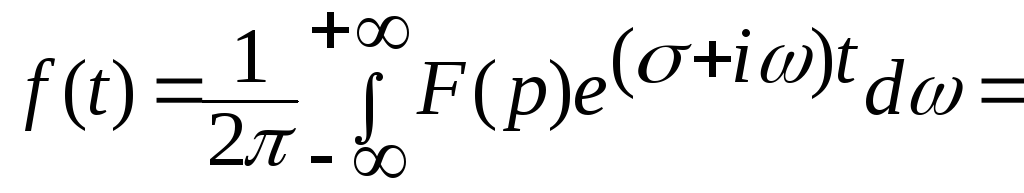
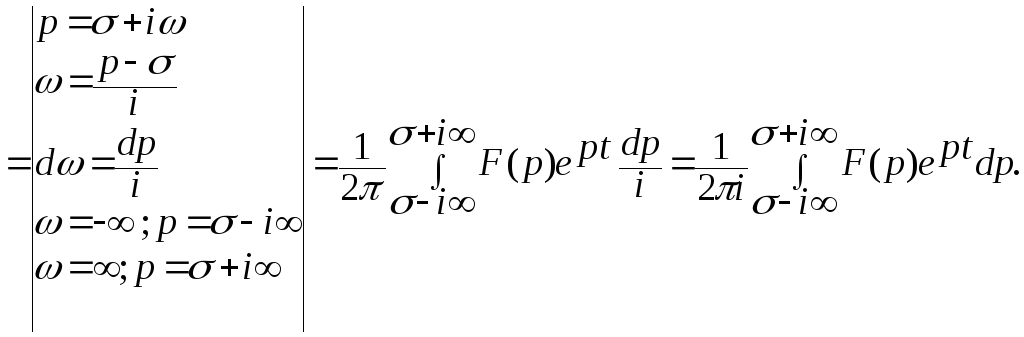
Итак, получим формулу:

(7.1)

где интегрирование производится по любой бесконечной прямой , лежащей в полуплоскости абсолютной сходимости интеграла Лапласа (т.е. левее) (рис.7.1).

Формула (7.1) является формулой обратного преобразования Лапласа. Еще ее называют формулой Римана-Мелина. Пользуясь этой формулой можно найти оригинал, соответствующий данному изображению. Отметим, что несобственный интеграл, стоящий справа понимается в смысле главного значения

Вычисление интеграла (1) для произвольных аналитических функций F(p) представляет большие трудности, поэтому будем рассматривать важные для нас частные случаи, которые исчерпывают наши потребности в вычислениях f(t).