
- •Введение
- •1. Понятие оригинала
- •2. Изображение по лапласу
- •3. Изображения простейших элементарных функций
- •4.Свойства преобразования лапласа
- •2С) Теорема подобия
- •3C) Теорема затухания (Теорема смещения)
- •5C) Теорема опережения.
- •10С) Интегрирование изображений.
- •11С) Теорема умножения изображений (теорема Бореля)
- •12С) Умножение оригиналов.
- •5.Примеры нахождения изображений с помощью таблиц 1 и 2
- •6. Импульсные функции и их изображения
- •7.Формула обращения преобразования лапласа
- •1)Тождественные преобразования и применение таблиц 1 и 2.
- •2) Вычисление оригиналов с помощью вычетов.
- •8.Применение преобразования лапласа для решения уравнений и систем
- •8.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.2 Решение дифференциальных уравнений с постоянными коэффициентами с помощью интеграла Дюамеля.
- •8.3 Решение дифференциальных уравнений с переменными коэффициентами.
- •8.4 Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
- •8.5 Линейные дифференциальные уравнения с запаздывающим аргументом.
- •8.6 Интегральные уравнения типа «свертки».
- •8.7 Линейные интегро-дифференциальные уравнения.
- •9.Решение диференциальных уравнений в частных производных и задач математической физики
- •10. Применение операторных методов для анализа линейных систем
- •11. Дискретное преобразование лапласа. Z – преобразование лорана
- •1) Решетчатые функции.
- •2) Конечные разности решетчатых функций.
- •3) Суммирование решетчатых функций.
- •4) Определение дискретного преобразования Лапласа.
- •5) Формула обращения.
- •1С) Теорема линейности.
- •Библиографический список
- •Оглавление
8.6 Интегральные уравнения типа «свертки».
Интегральным уравнением называется уравнение, содержащее искомую функцию под знаком интеграла.
Например,
![]() (8.10)
(8.10)
-это линейное интегральное уравнение Фредгольма второго рода.
Здесь y(x) – неизвестная функция,
f(x) и r(x,t) – заданные функции.
Функцию r(x,t) называют ядром уравнения (8.10),
a и b=const.
Изменим (8.10) следующим образом.
![]() (8.11)
(8.11)
Получим линейное интегральное уравнение Вольтерра 2го рода.
Если
в (8.10) и (8.11)
![]() ,
то уравнения будут называться однородными.
,
то уравнения будут называться однородными.
Если искомая функция y(x) входит только под знак интеграла, то (8.10) и (8.11) преобразуются в уравнения Фредгольма и Вольтерра 1го рода.
![]() или
или
![]() .
.
Совершенно очевидно, что большую роль в решении будет играть ядро уравнения, т.е. функция r(x,t). Важный класс уравнений Вольтерра получается, если ядро r(x,t) зависит только от разности
r(x,t)=r(x-t).
Уравнение в этом случае имеет вид.
![]() (8.12)
(8.12)
Его еще называют уравнением типа свертки.
Пусть входящие в уравнение (8.12) функции удовлетворяют условиям оригинала, тогда может быть найдено изображение функций по Лапласу
![]()
![]()
![]()
Пользуясь формулой свертки, получим операторное уравнение
![]() .
.
Откуда
![]() .
.
Для
Ф(р)
находим
![]() - решение интегрального уравнения
(8.12).
- решение интегрального уравнения
(8.12).
Пример. Решить интегральное уравнение
![]() .
.
Решение:

Так же решаются и системы интегральных уравнений.
Пример. Решить систему интегральных уравнений
 в
области изображений получим:
в
области изображений получим:
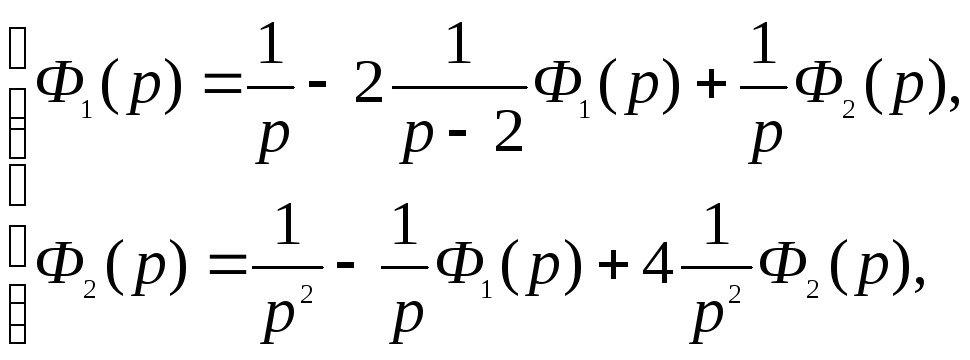 преобразовав,
будем иметь:
преобразовав,
будем иметь:
 или,
или,
 решим
методом Крамера:
решим
методом Крамера:
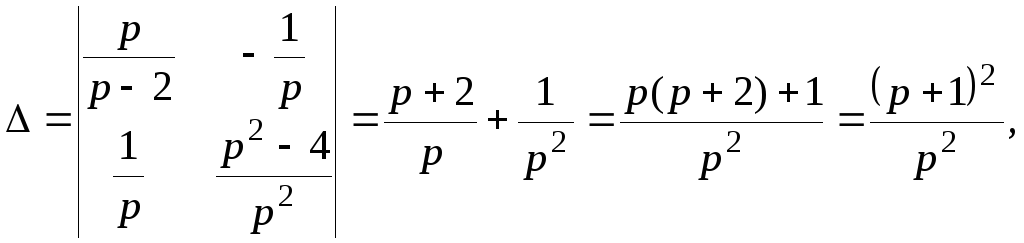
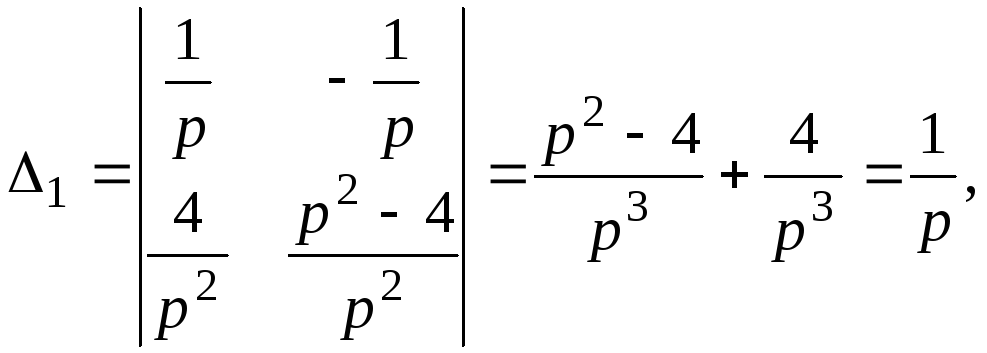
![]()
![]()


8.7 Линейные интегро-дифференциальные уравнения.
Линейными интегро-дифференциальным уравнением называется уравнение вида:
![]() ,
,
где
![]() - известные функции,
- известные функции,
![]() -
неизвестная функция.
-
неизвестная функция.
При решении таких уравнений ставятся начальные условия:
![]()
Если
все
![]() ,
то не нарушая общности можно получить
,
то не нарушая общности можно получить![]() ,
кроме того, будем рассматривать ядра
типа
,
кроме того, будем рассматривать ядра
типа![]() и тогда
и тогда
![]() .
.
Если,
все входящие в последнее уравнение
известные функции являются оригиналами,
то и искомая функция
![]() является оригиналом и можно применить
операторный метод решения.
является оригиналом и можно применить
операторный метод решения.
Пример: Решить уравнение
![]() ,
,
при
начальных условиях:
![]() .
.
Решение:
![]()

![]()
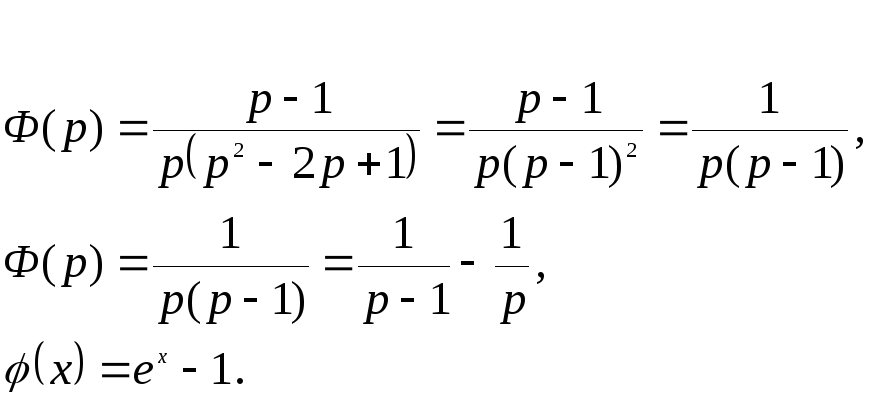
9.Решение диференциальных уравнений в частных производных и задач математической физики
Методы операционного исчисления, основанные на идее использования преобразования Лапласа являются наиболее эффективным при решении основных задач для дифференциальных уравнений в частных производных.
Неизвестная
функция
![]() ,
удовлетворяющая дифференциальному
уравнению в частных производных и
заданным условиям, может быть определена
с помощью однократного
либо
двукратного
преобразования
Лапласа.
,
удовлетворяющая дифференциальному
уравнению в частных производных и
заданным условиям, может быть определена
с помощью однократного
либо
двукратного
преобразования
Лапласа.
В первом случае преобразование Лапласа применяют к дифференциальному уравнению в частных производных по одной из двух независимых переменных в предположении, что другая остается неизменной. Полученное обыкновенное дифференциальное уравнение относительно изображения искомой функции интегрируется не операционным методом, а классическим. Возвращаясь от полученного изображения к оригиналу, находим решение поставленной задачи.
Во
втором случае к обыкновенному
дифференциальному уравнению относительно
изображения искомой функции опять
применяют преобразование Лапласа, но
по другой независимой переменной. В
результате получают алгебраическое
уравнение, из которого находят «двукратное»
изображение искомой функции. С помощью
двух обратных преобразований Лапласа
восстанавливается искомая функция
![]()
Решение дифференциального уравнения, найденное с помощью двукратного преобразования Лапласа, не зависит от того, в какой последовательности применялись прямые и обратные преобразования.
Удачно выбранный порядок в двукратном преобразовании может значительно облегчить решение задачи.
Операционный метод удобнее применять при решении задач математической физики, если:
начальные условия нулевые;
существуют изображения для всех функций, входящих в уравнение;
изображение искомого решения удовлетворяет следующим условиям:
![]()
![]()
![]()
Пример 1
Найти
решение уравнения
![]() ,
если
,
если
![]()
![]()
![]()
Применим
преобразование Лапласа по переменной
![]() ,
тогда
,
тогда
![]()
![]()
![]()
Заданное уравнение примет вид:
![]()
и решим методом Бернулли.
Согласно этому методу,
![]()
![]()
Осуществляя данную подстановку в уравнение, получим
 или
или

Решая первое уравнение системы, получим
![]() или
или
![]()
Подставим найденную функцию W во второе уравнение, будем иметь:
![]()
Откуда
![]()


Тогда
![]()
Так как
![]() -
изображение
по Лапласу, то
-
изображение
по Лапласу, то
![]() и тогда принимаемС=0,
то есть
и тогда принимаемС=0,
то есть
![]()
Возвращаясь к оригиналу, получим
![]()
Пример 2.
Найти
решение уравнения
![]() ,
удовлетворяющее условиям
,
удовлетворяющее условиям![]() ,
,![]()
Сначала
применим преобразование Лапласа по
переменной
![]() ,
получим
,
получим
![]()
Условие
![]() примет вид
примет вид
![]()
Применим
преобразование Лапласа еще раз, но уже
по переменной
![]() ,
получим
,
получим
![]()
Это
алгебраическое уравнение относительно
«двукратного» изображения -![]()
Решим его:
![]()
Возвращаясь к оригиналу по p, получаем:
![]()
Возвращаясь к оригиналу по q, получаем:
![]()
Пример 3.
Найти
формулу колеблющейся струны, закрепленной
на концах, если начальные скорости ее
точек равны нулю, а начальные отклонения
заданы соотношением
![]()
Подстановка
задачи: найти решение уравнения
![]()
![]() ,
,![]() ,
неравное тождественно нулю, удовлетворяющее
граничным условиям:
,
неравное тождественно нулю, удовлетворяющее
граничным условиям:
![]()
![]()
Будем решать эту задачу методом Лапласа. Применим преобразование Лапласа по переменной t, предварительно переписав уравнение в виде
![]()
Будем иметь
![]()
![]()
Граничные условия при этом примут вид:
![]()
Относительно
изображения искомого решения – функции
![]() получим обыкновенное дифференциальное
уравнение второго порядка, неоднородное,
с правой частью специального вида. Его
решение
получим обыкновенное дифференциальное
уравнение второго порядка, неоднородное,
с правой частью специального вида. Его
решение
![]()
где
![]() - общее решение однородного уравнения
- общее решение однородного уравнения
![]()
Составим и решим характеристическое уравнение
![]()
Тогда общее решение однородного уравнения примет вид
![]()
![]() -
частное решение неоднородного уравнения.
Его вид с точностью до неопределенных
коэффициентов будет
-
частное решение неоднородного уравнения.
Его вид с точностью до неопределенных
коэффициентов будет
![]()
Для нахождения B и C вычислим:
![]()
![]()
и подставим в уравнение:
![]() Отсюда
имеем:
Отсюда
имеем:
![]()
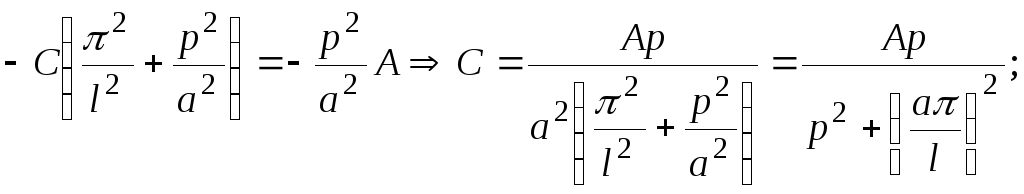
Тогда

Для нахождения С1 и С2 удовлетворим граничным условиям:

Очевидно, что С1= С2=0.
Таким
образом, имеем

Возвращаясь к оригиналу, получим:
![]()
Пример 4.
Найти
решение уравнения теплопроводности
![]() , удовлетворяющие начальному условию
, удовлетворяющие начальному условию![]() ,
где
,
где![]() и граничным условиям
и граничным условиям![]() и
и![]() .
.
Применяя к уравнению теплопроводности преобразование Лапласа по переменной t, получим:
![]()
Граничные условия при этом примут вид:
![]()
![]()
Перепишем полученное обыкновенное дифференциальное уравнение в виде:
![]()
Его
общее решение:
![]()
где
![]() -
общее решение однородного уравнения
-
общее решение однородного уравнения
![]()
Составим и решим характеристическое уравнение:
![]()
Тогда
![]()
Второе
слагаемое
![]() есть частное решение неоднородного
уравнения.
есть частное решение неоднородного
уравнения.
![]()
Оно
имеет вид
![]() .
.
Тогда
![]()
![]()
Подставляя в уравнение, находим:
![]()
![]()
Отсюда
![]()
Тогда
![]()
Удовлетворим граничным условиям:
![]()
![]()
При этом
![]()
Возвращаясь к оригиналу, получим:
![]() или
или
![]()
