НИРС Андреев / МНИ

Проверка его адекватности с использованием критерия Фишера показала, что в диапазонах изменения Res= (0,8364÷1,533) 107; H =0,2345÷1,2 и z = 0,1586 ÷ 0,8414 оно достаточно точно описывает опытные данные.

Дробный факторный эксперимент. Во многих практических задачах взаимодействия второго и высших порядков отсутствуют или пренебрежимо малы. Кроме того, на первых этапах исследования часто нужно получить в первом приближении лишь линейную аппроксимацию изучаемого уравнения связи при минимальном числе экспериментов. Поэтому использовать полный факторный эксперимент для определения коэффициентов лишь при линейных членах и парных произведениях неэффективно из-за реализации большого числа опытов (2N), особенно при большом числе факторов N. При увеличении числа независимых переменных N число опытов (число точек в плане) растет по показательной функции, т.е. число оцениваемых коэффициентов N+1 становится меньше числа точек плана 2N, в результате чего остается излишне много степеней свободы на проверку гипотезы адекватности. Раз-

ность vR = 2 N - (N +1) будет в этом случае характеризовать избыточность плана; например, vR =1 при N = 2; vR =11 при N = 4; vR = 57 уже при N = 6

и т.д.

Полная матрица планирования (см. табл. 8.3) позволяет рассчитать восемь коэффициентов уравнения. Если есть основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной зависимостью, то достаточно определить четыре коэффициента b0, b1 ,b2 , и b3 уравнения

y = b0 + b1x1 + b2 x2 + b3 x3 .

(8.13)

Для решения этой задачи можно ограничиться четырьмя опытами, если в планировании ПФЭ для двух факторов (22) использовать столбец табл. 8.5

x1 x2 в качестве плана для х3 (табл. 8.6).
Таблица 8.5	Таблица 8.6

v	x0	x1	x2	x1x2
1	+1	-1	-1	+1
2	+1	+1	-1	-1
3	+1	-1	+1	-1
4	+1	+1	+1	+1

v	x0	x1	x2	х3
1	+1	-1	-1	+1
2	+1	+1	-1	-1
3	+1	-1	+1	-1
4	+1	+1	+1	+1

Такой сокращенный план – половина ПФЭ 23 – носит название полуреплики от ПФЭ 23. Пользуясь таким планированием, можно определить свободный член и три коэффициента уравнения регрессии при линейных членах.

Если коэффициенты регрессии при парных произведениях не равны нулю, то найденные коэффициенты b будут смешанными оценками для теоретических коэффициентов b :

91

b1 ® b1 + b23 ; b2 ® b2 + b13 ; b3 ® b3 + b12.

(8.14)

Таким образом, сокращение числа опытов приводит к получению смешанных оценок для коэффициентов. Для того чтобы определить, какие теоретические коэффициенты смешаны, удобно пользоваться таким приемом:

поставив x3						на место x1x2 , получим соотношение x3 = x1x2 ,		называемое ге-
нерирующим						соотношением.	После умножения его на	х3	получаем
x 2	= x x	2	x	3	. Учитывая, что x 2		=1 (х3 равняется + 1 или –1), получаем
3	1					3	1 = x1x2 x3 .		(8.16)

Это произведение носит название определяющего контраста; с его помощью удобно определять, в каких столбцах содержатся одинаковые элементы, т.е. какие коэффициенты смешаны.

Умножив по очереди определяющий контраст на х1, х2, х3 найдем

x = x 2 x		2	x	3	= x	2	x	3	; x	2	= x x	3	;	x	3	= x x	2	.
1	1										1					1

Полученным соотношениям соответствует система смешанных оценок (8.14), т.е. b1 смешан с b23 , b2 -b13 , b3 -b13 .

При использовании дробного факторного эксперимента (ДФЭ) необходимо иметь четкое представление о так называемой разрешающей способности дробной реплики, т. е. определить заранее, какие коэффициенты являются несмешанными оценками для соответствующих теоретических коэффициентов. Тогда в зависимости от поставленной задачи подбирается дробная реплика, с помощью которой можно извлечь максимальную информацию из эксперимента. Например, в задаче с четырьмя факторами (N = 4) в качестве генерирующего соотношения можно взять x4 = x1 x2 x3 или любой из эффек-

тов двойного взаимодействия, например x4 = x1 x2 .

Воспользовавшись определяющим контрастом 1 = x1x2 x3 x4 , получим

такую систему смешанных оценок:

b1 ® b1 + b234 ;b2 ® b2 + b134 ;b3 ® b3 + b124 ;b4 ® b4 + b123; b12 ® b12 + b34 ;b13 ® b13 + b24 ;b14 ® b14 + b23.

В реальных задачах тройные взаимодействия бывают равными нулю значительно чаще, чем двойные. Значит, если нас более всего по физическому смыслу задачи интересуют оценки для линейных эффектов, следует выбирать генерирующее соотношение x4 = x1x2 x3 .

При генерирующем соотношении x4 = x1x2 определяющий контраст выражается соотношением 1 = x1x2 x4 . Получается следующая система оценок

b1 ® b1 + b24; b2 ® b2 + b14; b3 ® b3 + b1234 ; b4 ® b4 + b12;

b13 ® b13 + b234;b23 ® b23 + b134;b34 ® b34 + b123.

Следовательно, дробную реплику с генерирующим соотношением x4 = x1x2 имеет смысл использовать, если нас более всего интересуют коэф-

92

фициенты b13 ,b23 и b34 .- Применяют дробные реплики и большей степени

дробности (1/8 реплики, 1/4 реплики и т.п.).

Дробные реплики позволяют резко сократить число экспериментов для описания процесса. Следует иметь в виду, однако, что применение ДФЭ имеет весьма серьезный недостаток – исключаются из исследования некоторые взаимодействия факторов. Как правило, весьма затруднительно даже в практически известных процессах априорно установить отсутствие взаимодействия факторов. Поэтому использование ДФЭ, особенно большой дробности, требует весьма осторожного подхода.

Рассмотрим пример использования дробного факторного эксперимента. Исследования тепло-массообмена при конденсации химически реагирующего газа на основе теории подобия показали, что процесс можно описать уравнением подобия вида

~

~

~

~

~

~

~

æ m¢ ö

b6

Nu

b

b

2 K

b

Re

b

4

r

-b

(8.17)

D

= b Ar

1 Sc

x

3

5

ç ÷ ,

0

T

è m ø

где NuD – диффузионное число Нуссельта; члены в правой части характеризуют влияние отдельных факторов на процесс (Аr – свободной конвекции, Sc

–переносных свойств газовой смеси, Кх – кинетики химических реакций, ReT

–отводимого теплового потока, r – концентрации неконденсируемого газа, m¢/ m – трения на границе раздела жидкой и газообразной фаз).

Для определения коэффициентов уравнения применим метод планирования. Прологарифмировав (8.17) и перейдя от натуральных значений факто-

ров

~

æ

~

~

~

= ln K

~

= ln Re

~

~

= ln

m¢ ö

x

ç x

= ln Ar; x

= ln Sc; x

; x

; x

= ln r; x

÷ к ко-

i

è

1

2

3

x

4

T

5

6

m ø

дированным значениям xi согласно формуле преобразования (8.4), получим следующее линейное уравнение регрессии процесса:

					6
			y = b0		+ åbi xi ,	(8.18)
					i =1
где	~	6	~ ~	;bi	~ ~
	y = ln NuD ;b0 = ln b0	+ åbi xi0			= bi Dxi .

i =1

Поскольку зависимость (8.18) линейная, для определения величин b0 и

bi можно составить ортогональный план первого порядка на основе 1/8 реплики ПФЭ для шести факторов с числом опытов, равным 26-3=8. При этом

будем

использовать

следующие

генерирующие

соотноше-

ния: x4 = x1x2 x3; x5 = x1x2 ; x6 = x1x3. Матрица

планирования

приведена в

табл. 8.7.

Таблица 8.7

v

x0

x1

x2

x3

x4

x5

x6

y

93

1	+	-	-	-	-	+	+	y1
2	+	+	-	-	-	-	-	y2
3	+	-	+	-	+	-	+	y3
4	+	+	+	-	-	+	-	y4
5	+	-	-	+	+	+	-	y5
6	+	+	-	+	-	-	+	y6
7	+	-	+	+	-	-	-	y7
8	+	+	+	+	+	+	+	y8

Проведение опытов, обработка опытных данных с целью получения коэффициентов уравнения (8.18) и их статистический анализ выполняются в такой же последовательности, как и в предыдущем примере.

8.4. Планирование второго порядка

Часто для описания поверхности отклика полинома первого порядка уже недостаточно. Во многих случаях вполне удовлетворительная аппроксимация может быть достигнута, если воспользоваться полиномом второго порядка. Уравнение регрессии второго порядка имеет вид

N	N
M {y}= h = b0 + åbi xi +	å biu xi xu
i =1	i,u =1
	i <u

N
+ åbii xi2.	(8.19)

i =1

Основное требование к плану второго порядка состоит в том, что план должен допускать получение раздельных, не смешанных оценок коэффициентов регрессии. Для этого необходимо, чтобы число разных опытов было не меньше числа коэффициентов в уравнении регрессии, равного числу сочета-

ний из N+2 по два, т.е. K ³	(N + 2)(N +1) = C 2		. Кроме того, требуется,
	2	N +2

чтобы каждый фактор варьировался не менее чем на трех уровнях.

Полный факторный эксперимент 3N содержит слишком большое число опытов (N=3, 3N=27; N=4, 3N=81; N=5, 3N=243). Сократить число опытов можно, если воспользоваться так называемыми композиционными или последовательными планами, предложенными Боксом и Уилсоном. «Ядро» таких планов составляет ПФЭ 2N при N<5 или дробная реплика от него при N≥5. Согласно этим планам, если линейное уравнение регрессии оказалось неадекватным, необходимо добавить 2N «звездных» точек, расположенных на координатных осях факторного пространства (±а, 0, ..., 0), (0, ±а, .., 0), ..., (0, 0, ±а), где а – расстояние от центра плана до «звездной» точки – «звездное» плечо, и увеличить число экспериментов в центре плана К0 Такие планы называются центральными, ибо все опыты расположены симметрично вокруг основного уровня эксперимента, и композиционными, т.е. последовательно строящимися, а сокращено ЦКП.

94

Общее число опытов в матрице композиционного плана при N факторах составит K = 2 N + 2N + K0 для N<5 и K = 2 N -1 + 2N + K0 для N≥5.

Ортогональные планы. Композиционные планы легко проводятся к ортогональным выбором «звездного плеча» а. При числе факторов N=2 а выбирается равным 1,0, при N=3 а = 1,215, при N=4 а= 1,414, при N = 5 а=1,547 (здесь величина а приведена для случая, когда в качестве генерирующего со-

отношения в дробной реплике 25-1 используется x5 = x1x2 x3 x4 ). Обычно К0 в

этом случае принимают равным единице.

Ротатабельные планы. Для того чтобы композиционный план был ротатабельным, величину «звездного» плеча а выбирают из условий a = 2 N / 4 (N < 5), a = 2(N -1)/ 4 (N ³ 5). Число точек в центре плана К0 увеличивают (например, при N=2 K0 выбирают равным 5, при N = 3 К0=6, при N=4

К0=7, при N=5 K0 =10).

8.5. Планирование экстремальных экспериментов

Изменяя условия процесса, можно получить значения того или иного отклика и при необходимости оптимизировать процесс по этому отклику, принятому за критерий или параметр оптимизации. Для решения задач оптимизации используются два принципиально различных подхода:

1)каким-либо способом определяется полная математическая модель и далее задача решается аналитическим или численным методом;

2)осуществляется экспериментальный поиск экстремальной точки в факторном пространстве переменных x1, x2 ,..., xN в процессе эксперимента;

местоположение этой точки в факторном пространстве определяется векто-

ром х0.

Первый подход рассматривается в литературе по методам оптимизации. Здесь же остановимся подробнее на методах второй группы. Экстремальное значение отклика в них достигается с помощью многократной последовательной процедуры изучения поверхности и продвижения в факторном пространстве. Методы различаются способом определения направления движения и организацией самого движения.

Для отыскания точки максимума можно воспользоваться методом сечений (методом Зайделя – Гаусса). По этому методу выбирается произвольная точка М0, фиксируются все переменные, кроме одной, и отыскивается точка М1, соответствующая условному экстремуму при x2 = x2,1, затем фик-

сируется переменная x1 = x1,2 и отыскивается точка М2 и т.д. Поиск оптиму-

ма здесь не только малоэффективен, но и весьма длителен и удлиняется при увеличении числа факторов, причем при определенной форме зависимости у от факторов поочередное изменение аргументов может привести к ошибке в определении экстремума. На рис. 8.7 показан один из таких частных случаев, когда поочередное изменение каждого из двух аргументов в любую сторону

95

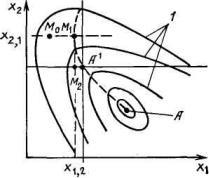
(вдоль осей координат) от точки A1 вызывает уменьшение у (отклик у откладывается перпендикулярно к плоскости рисунка). Из-за этого создается ложное впечатление, что точка А1 соответствует максимуму, в то время как в действительности максимум у (точка А) располагается при больших значениях x1 и меньших значениях х2. Рассмотрим более совершенные методы.

Рис. 8.7. Схема движения к оптимуму методом Зайделя– Гаусса: А' – ложный оптимум; А – действительный оптимум;

1 – линии постоянного уровня

Метод градиента. При оптимизации процесса этим методом рабочее движение совершается в направлении быстрого возрастания выходного параметра, т.е. в направлении градиента целевой функции y(х). Причем направление движения корректируется после каждого рабочего шага, т.е. каждый раз заново вычисляется значение вектора grad y(x) по результатам специально спланированных пробных экспериментов.

Координатами вектора градиент

	grad y(x)=	¶y	i +	¶y		j +... +	¶y		k	(8.20)
		¶x		¶x	2		¶x	N
		1

служат коэффициенты при линейных членах разложения функции у(х) в ряд Тейлора по степеням xi (i =1,2,..., N ).В выражении (8.20) i, j, ..., k –единичные

векторы вдоль координатных осей xi. Тогда соответствующие компоненты вектора градиента могут быть получены как коэффициенты b1, b2 , ..., bN линейной аппроксимации поверхности отклика вблизи исходной точки х:

y(x)= b0 + b1x1 + b2 x2 +... + bN xN .	(8.21)
Для получения оценок линейных коэффициентов b0 , b1, ... bN	можно

воспользоваться любым из известных способов экспериментального получения уравнения (8.21) (например, можно реализовать ПФЭ с центром в точке

xi).

По результатам пробного эксперимента вычисляется вектор

grad y(x1 )= b1i + b12i +... + b1N k .	(8.22)
Совершается рабочий шаг в направлении grad y(x1)
x2 = x1 + a grad y(x1 ).	(8.23)

Здесь а – параметр рабочего шага.

96

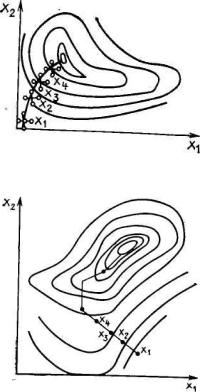
Рис. 8.8. Метод градиента для двух факторов

Рис. 8.9. Крутое восхождение для двух факторов

В точке х2 описанная выше процедура полностью повторяется. Поиск прекращается, когда модуль градиента у становится малой величиной

(|grad у(х) | ≈0), т.е. все коэффициенты bi, (i = 1, 2, ..., N) в уравнении (8.21)

получаются незначимыми.

Характер движения к оптимуму при использовании градиентного метода иллюстрирует рис. 8.8.

Существуют модификации метода градиента, в которых, например, параметр рабочего шага а зависит от номера шага, и некоторые другие. Следует отметить, что если целевая функция y сложная, то и градиентный метод приводит к значительным вычислительным трудностям.

Метод крутого восхождения. При использовании этого метода в отличие от градиентного корректировка направления производится не после

каждого следующего шага, а по достижении в некоторой точке хn, на данном направлении частного экстремума целевой функции (рис. 8.9) аналогично методу Гаусса – Зайделя. Важной особенностью процедуры крутого восхождения является также регулярное проведение статистического анализа промежуточных результатов на пути к оптимуму.

Практически поиск оптимума по методу крутого восхождения осуществляется в несколько этапов:

97

1) с центром в исходной точке x1 проводится ПФЭ (или ДФЭ)для определения grad y(x1); результаты эксперимента подвергаются статистическому анализу (проверяются значимость оценок коэффициентов линейного уравнения регрессии и адекватность этого уравнения);

2)вычисляется направление градиента;

3)проводятся несколько опытов в направлении градиента функции, выбирается опыт с наибольшим значением у; затем весь цикл повторяется.

Поиск прекращается, когда все коэффициенты bi, (i = l, 2, ..., N) линейного уравнения получаются незначимыми, что свидетельствует о выходе в область экстремума.

Рис. 8.10. Схема движения симплекса

Относительно выбора шага для движения по градиенту заметим, что слишком малый шаг потребует значительного числа опытов при движении к оптимуму, а большой шаг создает опасность проскакивания области оптимума.

Симплексное планирование. Последовательный симплексный метод планирования (ПСМ), является одним из эффективных методов поиска экстремума. В этом методе не требуется вычисления градиента, поэтому он относится к безградиентным методам поиска оптимума и связан с простыми расчетами при шаговом движении к оптимуму.

Симплекс – это простейший выпуклый многогранник, образованный N+1 вершинами в N-мерном пространстве. Так, например, на плоскости (N = 2) симплекс – любой треугольник, в трехмерном пространстве – любая треугольная пирамида и т.д.

Симплекс называется правильным или регулярным, если все расстояния между образующими его вершинами равны. Применение правильных симплексов упрощает процедуру последовательного расчета вершин симплекса.

Процедура ПСМ состоит в выборе начального симплекса и последовательном отражении его вершин с наихудшим откликом в новую точку относительно противоположной грани. Процесс заканчивается при достижении экстремальной области. Для N = 2 сущность симплексного метода движения к оптимуму для правильного симплекса можно иллюстрировать на примере рис. 8.10. Начальный симплекс (опыты 1, 2, 3) располагают в факторном пространстве на основе априорной информации об объекте исследования. Ре-

98

зультаты опытов в вершинах 1, 2, 3 упорядочивают, т.е. ранжируют по значению отклика, далее выбирают наихудший результат (пусть для примера это будет точка 1). Для первого шага к оптимуму на грани 2, 3, противоположной наихудшему опыту, симметрично строят новый правильный симплекс 2, 3, 4, опытные результаты опять ранжируют и т.д.

Координаты каждой новой вершины симплексов xuiн рассчитывают по формуле

H		2	æ N +1	*	ö	*
			ç		÷
xui	=		ç å xui - xui ÷			- xui ,	(8.24)
		N è u =1			ø

где N– число факторов; u– номер опыта, т.е. вершины симплекса (u = 1, 2, ..., N+1); i – номер фактора; xui* –координата i-фактора в наихудшем опыте (i= l,

2, ..., N).

По достижении области экстремума симплекс начинает вращение вокруг вершины с максимальным значением отклика. Здесь-необходимо прекратить процедуру ПСМ.

Важным свойством ПСМ является то, что он не боится ошибок эксперимента, которые могут лишь задержать, но не остановить продвижение к оптимуму. В связи с этим при ПСМ дублировать опыты не обязательно. Осложнения при применении ПСМ возникают тогда, когда симплекс попадает на гребень поверхности отклика, в этом случае он начинает колебаться. В схеме оптимизации, изображенной на рис. 8.10, такое колебание возникает при достижении области оптимуму – симплекс 9, 10, 11 возвращается на место предыдущего 9, 10, 8.

В случае, когда колебание возникло на гребне вне оптимума, для устранения колебаний рекомендуется отражать не самую худшую вершину, а ближайшую, несколько лучшую в ранжированном ряду откликов.

При достижении оптимальной области можно уточнить при необходимости положение оптимума (если отсутствует его дрейф). Для этого можно использовать в этой области симплекс меньших, размеров или применить ЦКП второго порядка.

Симплексный метод широко используется для поиска оптимума как на реальных объектах, так и по математической модели. Эта эффективность по сравнению с другими методами тем заметнее, чем больше число факторов.

8.6. Определение динамических характеристик объектов при активном эксперименте

В инженерной практике свойства энергетических объектов (теплообменники, деаэраторы, котельные установки и др.) обычно выявляют экспериментальным путем. С этой целью технологический объект оснащают аппаратурой для нанесения входных типовых возмущений и определения его ответной реакции во времени. При этом предусматривают: планирование и подготовку эксперимента, проведение эксперимента с целью нахождения

99

временных или частотных характеристик и обработку полученных экспериментальных зависимостей.

Снятие временных характеристик проводят на реальном объекте, оснащенном аппаратурой в соответствии со схемой, приведенной на рис. 8.11. Все измерительные преобразователи и исполнительные устройства обычно относят к объекту. Быстродействие всех элементов используемой аппаратуры в целом должно значительно превышать быстродействие объекта.

Для снятия временных характеристик объект исследования приводят в равновесное состояние, а затем с помощью панели дистанционного управления и исполнительного устройства наносят на вход объекта возмущающее воздействие известной формы (ступенчатое или импульсное). Реакция объекта на это возмущение (кривая разгона или импульсная характеристика) регистрируется в координатах: выходная величина – время.

Рис. 8.11. Схема установки аппаратуры для определения временных (или частотных) характеристик объекта:

1 – панель дистанционного управления (или генератор гармонических колебаний); 2 – исполнительное устройство; 3 – исследуемый объект; 4, 6 – измерительные преобразователи выходной и входной величин соответственно; 5 – регистрирующий прибор

Снятие кривой разгона предусматривает нанесение на объект ступенчатого возмущения путем энергичного изменения степени открытия проходного сечения регулирующего органа; при этом отмечают величину и момент нанесения возмущения. Изменение выходной величины регистрируют до тех пор, пока объект не примет нового установившегося значения (объект устойчивый) или пока скорость изменения выходной величины не станет постоянной (объект нейтральный).

Кривые разгона обычно определяют на действующем (находящемся в промышленной эксплуатации) объекте, изменяя его входную величину на несколько процентов. Использование такого сравнительно небольшого возмущения обусловлено тем, что реакция объекта не должна выходить за пределы ограничений, установленных технологическими соображениями.

Снятие импульсной характеристики предусматривает нанесение на объект импульсного возмущения последовательного в виде двух ступенчатых возмущений, равных по величине, но противоположных по направлению, с интервалом по времени Dt. Изменение выходной величины регистри-

100