НИРС Андреев / МНИ

маги, имитирующее термическое сопротивление теплоотдачи RaT = 1/ a . Дополнительное электрическое сопротивление Ra и длина дополнительного

слоя бумаги определяются из равенства теплового и электрического аналога чисел Био; в случае, когда это дополнительное сопротивление изготавливается из той же электропроводной бумаги, из которой изготовлена модель, длина дополнительного слоя бумаги будет определяться соотношением lдоп = RasS = C1l/ a; в случае, когда модель изготовлена из бумаги с удель-

ным электрическим сопротивлением rм, а дополнительное сопротивление из

бумаги с rдоп, геометрический размер - l	доп	=C	rм	l .
		l rдоп a

Задание граничных условий IV рода обеспечивается непосредственным соединением (например, путем склеивания электропроводным клеем) соответствующих поверхностей двух участков модели. При решении задач теплопроводности для многослойных стенок, состоящих из слоев с разными коэффициентами теплопроводности ( l1 , l2 , l3 и т.д.), электрическая модель из-

готавливается из разных сортов электропроводной бумаги, удельное электрическое сопротивление которых связано друг с другом так же, как и коэффициенты теплопроводности слоев (r 2 / r1 = l1 / l 2 ); r3 / r1 = l1 / l3 и

т.д.).

Модели из электропроводной бумаги, обеспечивая достаточную точность (погрешность 2-5 %) и наглядность решения при приемлемой трудоемкости, обладают рядом недостатков, наиболее важными из которых являются: сложность обеспечения и изменения граничных условий (особенно II и III рода), а также изменение во времени из-за старения электропроводных свойств бумаги и используемого при монтаже модели клея. От этих недостатков свободны электрические модели, создаваемые из сеток электрических сопротивлений.

3.3. Моделирование температурных полей на R- и RC-сетках

Моделирование непрерывного температурного поля электрическими сетками с сосредоточенными параметрами равнозначно переходу от решения дифференциального уравнения теплопроводности к решению его конечноразностной аппроксимации. В этом случае производные в дифференциальном уравнении заменяют приближенными значениями, выраженными через соотношения разностей соответствующих величин в отдельных дискретных точках (узлах расчетной сетки).

Сущность моделирования нестационарных температурных полей электрическими сетками рассмотрим на примере однородной плоской стенки тол-

щиной d с одномерным нестационарным температурным полем (рис. 3.1, а).

21

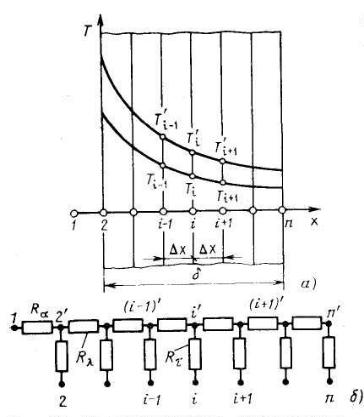
Рис. 3.1. К моделированию температурного поля на R-сетках:

а- схема разбивки стенки расчетной сеткой;

б– электрическая модель (R- сетка)

На левой поверхности (x = 0) задано граничное условие III рода на (коэффициент теплопередачи s и температура омывающей стенку жидкостей

T f ), а на поверхности	x = d	æ	¶T ö	= 0. На-
		задано условие теплоизоляции ç	÷
		è	¶x øx=d

чальное условие имеет вид: при t = 0 T = T (x).

Для стенки с постоянными физическими свойствами (а = const) дифференциальное уравнение теплопроводности будет иметь вид

¶T	= a	¶2T	,	(3.13)
¶t		¶x2

где Т – температура; х – координата; a = l /(rc)– коэффициент температуро-

проводности; l – коэффициент теплопроводности; r – плотность; с – теплоемкость.

3.4. Электрогидродинамическая аналогия.

Электрогидродинамическая аналогия (ЭГДА) – это аналогия между потенциальным течением жидкости (потенциальным называется безвихревое течение идеальной (невязкой) жидкости, когда составляющие скорости могут

22

быть выражены через потенциал скорости.) и течением электрического тока в проводящей среде. Эти явления описываются одинаковыми по форме дифференциальными уравнениями Лапласа.

Для несжимаемой жидкости и для проводящей среды с постоянной электропроводностью эти уравнения имеют вид

¶2j + ¶2j + ¶2j = 0 ; ¶хr2 ¶yr2 ¶zr2

¶2u + ¶2u + ¶2u = 0 ¶х2 ¶y 2 ¶z 2

(3.14)

(3.15)

Здесь j - потенциал скорости; u - электрический потенциал; индекс «r» относится к координатам гидродинамического явления.

Как видно из уравнений (3.14) и (3.15), потенциал скорости j и электрический потенциал и являются параметрами-аналогами. Это означает, что изучение потенциального течения жидкости в гидродинамической системе может быть заменено изучением распределения электрического потенциала на электрической модели.

В случае плоского потенциального течения жидкости поле электрического потенциала и

	¶2u	+	¶2u	= 0		;	(3.16)
	¶х2		¶y 2
	моделирует не только поле потенциала скорости j
	¶2j	+	¶2j		= 0	;	(3.17)
	¶хr2		¶yr2
	но и поле функции тока y
	¶2y	+	¶2y		= 0		(3.18)
	¶хr2		¶yr2

Следовательно, в этом случае имеют место два типа аналогии: аналогия и – j, когда электрический потенциал и моделирует потенциал скорости j; аналогия и – j, когда электрический потенциал и моделирует функцию тока y.

Целесообразность применения того или иного типа аналогии для решения аэрогидродинамических задач определяется в основном трудоемкостью и требованиями к точности изготовления электрических моделей обтекаемых тел. В случае применения аналогии и – j на поверхности обтекаемого тела

23

lo ).

и umax

- umin .

должно удовлетворяться условие ¶¶jn = 0 . Для реализации этого условия на

электрической модели обтекаемого тела модель должна быть изготовлена из диэлектрического материала. В случае применения аналогии и– y контур обтекаемого тела является линией тока, поэтому контур электрической модели обтекаемого тела должен быть линией равного потенциала и, следовательно, модель должна быть изготовлена из электропроводного материала.

Графическое представление картины обтекания с помощью линий тока (y= const) получается более наглядным, чем с помощью эквипотенциальных линий (j= const), поэтому рассмотрим далее аналогию и–y.

Для выявления условий, при которых явления в электрической модели и исследуемом объекте будут аналогичными, удобно воспользоваться безразмерными параметрами:

ymax - y

– относительное избыточное значение функции тока;

y =

ymax - ymin

umax - u

v =

– относительный избыточный электрический потенци-

umax - umin

ал;

=

xr

=

yr

x

, y

r

– относительные координаты в исследуемой гидро-

r

lor

lor

динамической системе;

=

x

,

=

y

x

y

– относительные координаты в электрической модели.

l

l

o

o

В первых двух безразмерных параметрах за масштаб преобразований приняты максимальные избыточные величины ymax - ymin

Относительные координаты получены делением их абсолютного значения на характерные линейные размеры в соответствующих системах ( lor ,

Дифференциальные уравнения (4.18) и (3.16) в безразмерной форме

имеют вид

¶2

+ ¶2

y

y

= 0 ;

(3.19)

¶

r2

¶

r2

х

y

¶2

¶2

v

+

v

= 0 .

(3.20)

¶

r2

¶

r2

х

y

Для того чтобы функции y и v , определяемые уравнениями (3.19) и (3.20), были одинаковыми, требуется тождественность безразмерных параметров, выражающих условия однозначности для гидродинамической системы и электрической модели.

Тождественность геометрических условий однозначности обеспечивается геометрическим подобием гидродинамической системы и электрической

24

модели, которое характеризуется масштабом геометрического моделирования Сl = l0/ l0r. В сходственных точках рассматриваемой системы безразмерные координаты численно равны ( xr = x; yr = y ).

Тождество физических условий однозначности в случае постоянных физических свойств гидродинамической системы (плотность жидкости) и электрической модели (электропроводность) является автомодельным, так как безразмерные значения физических свойств гидродинамической системы и электрической модели во всех точках равны единице.

Тождественность граничных условий однозначности обеспечивается численным равенством безразмерных параметров ( yгр = vгр ) во всех сходст-

венных точках границ системы и модели. При моделировании граничных условий на поверхности тела, обтекаемого потоком вязкой жидкости, принимают их такими же, как на внешней границе пограничного слоя.

Таким образом, тождественность уравнений (3.19) и (3.20), а также условий однозначности позволяет заключить, что

				y - ymin	=	u - umin
y = v или
							.	(3.21)
				ymax - ymin		umax - umin

Связь между размерными значениями этих параметров имеет следующую форму:

y = Kyu + const или Dy = KyDut ;

(3.22)

Ky = ymax - ymin . umax - umin

Электрическая модель позволяет построить линии тока y = const , кото-

рым на этой модели соответствуют линии постоянного потенциала v = const . Линия тока обладает тем свойством, что каждая частица жидкости, на-

ходящаяся на ней, имеет скорость, вектор которой направлен по касательной к этой линии в данной точке. При стационарном режиме течения линия тока совпадает с траекторией частицы, поэтому линию тока можно представить себе как непроницаемую стенку воображаемого канала, по которому течет жидкость: сужение канала указывает на ускорение, а расширение, наоборот,

– на замедление течения жидкости.

На взаимосвязи скорости и функции тока основано определение относительной скорости течения жидкости с помощью электрического моделирования.

На основе измерений, выполненных на электрической модели, можно вычислить также коэффициенты давления, коэффициент подъемной силы профиля и т.д.

Метод ЭГДА может применяться для исследования как плоских, так и пространственных течений жидкостей и газов с дозвуковыми скоростями. Моделирование плоских течений несжимаемых жидкостей осуществляется преимущественно на электропроводной бумаге, а иногда в ванне с электролитом. Для моделирования пространственных течений используют ванны с

25

электролитом, а для моделирования плоских течений газа с дозвуковыми скоростями – ванны с электролитом переменной глубины, при этом толщина слоя электролита изменяется в соответствии с изменением плотности газа.

Для решения аэродинамических задач наряду с ЭГДА применяют также магнитогидродинамическую аналогию (МАГА) и газогидравлическую аналогию (ГГА), причем последняя может быть использована как для дозвуковых, так и для сверхзвуковых течений газа.

Подчеркнем, что методы аналогий позволяют исследовать лишь потенциальное движение жидкости или газа – ни один из них не дает возможности смоделировать силы вязкости.

Контрольные вопросы

1.В чем заключается метод аналогий, используемых в научных исследованиях?

2.Какие виды аналогий используются в научных исследованиях?

3.Поясните метод электротепловой (ЭТА) аналогии.

4.Чем отличаются аналоговые вычислительные машины (АВМ) от цифровых вычислительных машин?

5.Охарактеризуйте электрогидродинамическую аналогию (ЭГДА) физических процессов.

4. МАТЕМАТИЧЕСКИЙ ЭКСПЕРИМЕНТ.

Математический эксперимент – это мощный метод исследования, основанный на численном решении уравнений, отписывающих физическое явление. Получение важных научных результатов на основе этого метода стало возможным только тогда, когда при его реализации стали использовать цифровые электронно-вычислительные машины (ЭВМ) - компьютеры. Поэтому математический эксперимент часто называют машинным, компьютерным (или численным).

ЭВМ позволяет решать широкий круг физических задач, имеющих математическое описание и неразрешимых аналитическим путем. Решение таких задач осуществляется с помощью специального математического аппарата – численных методов. Численные методы представляют собой определенную последовательность операций над числами, т.е. вычислительный алгоритм, позволяющий получить приближенное решение исходного уравнения или системы уравнений в виде совокупности числовых значений искомых величин, которая соответствует конкретным значениям влияющих параметров, входящих в условия однозначности задачи.

Характерной особенностью численных методов является большой объем вычислительной работы при их реализации, поэтому, хотя многие из этих методов были известны и ранее, получили широкое практическое использование лишь после появления ЭВМ, что, в свою очередь, привело к созданию новых методов, специально ориентированных на применение ЭВМ, и к раз-

26

витию их теории.

Численное исследование того или иного явления имеет много общего с физическим экспериментом. В том и другом случае результаты получаются в виде совокупности числовых значений параметров, а в дальнейшем могут быть обобщены на основе теории подобия; программа расчетного исследования, так же как и программа физических экспериментов, может быть разработана с использованием теории планирования экспериментов и т.д. При этом роль экспериментальной установки выполняет ЭВМ, а физическое явление заменяется его математическим описанием или, точнее, математической моделью. Последний термин более точен, поскольку, с одной стороны, всякое физическое явление бесконечно сложно, а наши знания о нем не являются абсолютными, поэтому в любом случае математически возможно описать лишь какую-то модель этого явления, соответствующую современному уровню знаний; с другой стороны, всегда целесообразно оперировать с наиболее простой моделью, отражающей, однако, важнейшие для рассматриваемой задачи стороны явлений, поэтому при формулировке задачи сознательно не принимаются во внимание многие несущественные особенности реального явления.

Возможности математического эксперимента как одного из способов исследования физических явлений в значительной степени определяются техническими характеристиками ЭВМ: быстродействием, объемом оперативной памяти и т.д.

Совершенствование вычислительной техники и развитие теории численных методов способствуют расширению круга задач, решение которых становится возможным на основе математического эксперимента. Особое значение математический эксперимент приобретает в случаях, когда решение задачи другими способами невозможно или чрезвычайно затруднено. Так, например, при исследовании процессов, протекающих при высоких температуре и давлении, когда зачастую физический эксперимент технически трудно осуществим или даже невозможен, математический эксперимент позволяет определить необходимые параметры системы. Предварительный численный эксперимент может избавить исследователя от риска, связанного с постановкой физического эксперимента при исследовании высокотемпературной плазмы и т.д. Во многих других случаях постановка математического эксперимента требует меньших материальных затрат по сравнению с экспериментом физическим.

Нередко из-за ограниченности наших знаний об окружающем мире математическая формулировка задачи оказывается незамкнутой. В результате численного исследования таких явлений, выполненного с привлечением различных гипотез для замыкания недостающих связей и последующего сопоставления результатов расчета с данными физического эксперимента, появляется возможность анализа достоверности той или иной гипотезы, а значит, и познания механизма протекающих процессов.

Процесс исследования физического явления с помощью математического эксперимента можно подразделить на четыре этапа:

27

·конструирование физической модели и ее математическая формулировка;

·разработка численного метода (вычислительного алгоритма) и его реализация в программе для ЭВМ;

·расчетное исследование;

·анализ полученных результатов и их обобщение.

Первый этап требует глубоких знаний закономерностей изучаемых явлений, проникновения в их взаимосвязи. Эти знания приобретаются при изучении фундаментальных и специальных дисциплин. Наиболее сложным и ответственным моментом на первом этапе является выбор тех сторон исследуемых явлений и их связей с другими явлениями, которые существенны для данной задачи и подлежат включению в математическую модель.

Различают феноменологические, асимптотические математические модели и модели ансамблей. Феноменологические модели возникают как результат прямого наблюдения, изучения и осмысления того или иного физического явления; асимптотическая модель получается как частный случай некоторой наиболее общей модели; модель ансамблей представляет собой результат обобщения или синтеза отдельных частных моделей.

На втором этапе, как правило, приходится заменять исходное уравнение или систему уравнений некоторыми другими уравнениями, которые позволяют построить численные методы их решения. При разработке численного метода исследователь сталкивается с целым рядом проблем. Во-первых, вычислительный алгоритм должен быть устойчивым, т.е. малые ошибки, допущенные на каком-либо этапе вычисления (например, при округлении числовых данных), при дальнейших вычислениях не должны иметь тенденции к существенному возрастанию. Во-вторых, численный метод должен обеспечивать сходимость к искомому решению. Дать строгое доказательство сходимости и устойчивости разработанного численного метода оказывается возможным далеко не всегда. В этой связи исследователь вынужден часто разрабатывать и использовать численный метод без строгого математического обоснования его применимости.

Наконец, численный метод должен разрабатываться с учетом возможностей вычислительной техники (быстродействия ЭВМ, объема памяти и т.д.), чтобы обеспечить проведение исследования в приемлемые сроки с приемлемыми затратами машинного времени.

При создании вычислительного алгоритма важно правильно выбрать соотношение в нем формализованных (предусмотренных программой) и неформальных процедур. Это связано с тем, что неразумно стремиться разработать универсальный алгоритм, способный преодолеть все возможные трудности поиска решения, обусловленные теми или иными особенностями исследуемого явления, поскольку, во-первых, высокая степень универсальности чрезмерна усложняет алгоритм и приводит к увеличению затрат машинного времени, а во-вторых, предусмотреть заранее все эти особенности попросту невозможно. Поэтому у исследователя должна быть возможность

28

вмешиваться в процедуру вычислений, внося при необходимости коррективы в алгоритм или исходные данные расчета (неформальная процедура). Такая возможность появляется при работе ЭВМ в режиме диалога человек – машина.

На третьем этапе математического эксперимента проводится серия расчетов, позволяющая получить решение поставленной задачи.

При анализе полученных результатов, проводимом на четвертом этапе математического эксперимента, уточняется программа исследований с целью детального изучения тех или иных особенностей явления. На этом же этапе после накопления и анализа достаточного количества информации о рассматриваемом явлении может быть сделано заключение о достоверности разработанной математической модели, границах ее применимости или необходимости ее совершенствования. В дальнейшем полученные результаты могут быть обобщены с использованием теории подобия и представлены в форме, удобной для проведения инженерных расчетов.

Можно выделить четыре источника погрешности математического эксперимента: математическая модель, исходные данные, численный ме-

тод и округления в процессе вычислений.

Погрешность математической модели связана с приближенностью математического описания физического явления, обусловленной как сознательной его схематизацией с целью упрощения задачи, так и относительностью и ограниченностью существующих знаний об окружающем мире. Количественно оценить эту составляющую погрешности результатов математического эксперимента можно лишь путем их прямого сопоставления с данными физического эксперимента. Однако провести такое сопоставление часто не представляется возможным. В этой связи условием достоверности математической модели следует считать ее удовлетворение критерию практики, при этом требование критерия практики – это не только соответствие полученных результатов прямому эксперименту, но и то, что полученные с помощью данной модели результаты способствуют достижению целей, стоящих перед исследователем.

Исходные данные задачи, как правило, неточны: например, это могут быть величины, найденные из эксперимента. Ошибка в задании исходных данных приводит к погрешности решения, которую называют неустранимой погрешностью. Эта составляющая погрешности математического эксперимента может быть определена по методике, используемой для оценки погрешности величин-функций.

Погрешность численного метода обусловлена заменой исходных уравнений, описывающих принятую модель физического явления, другими аппроксимирующими уравнениями, позволяющими построить вычислительный алгоритм, а также приближенностью методов решения этих аппроксимирующих уравнений. Численные методы обычно строятся так, что они содержат некоторый параметр, при стремлении которого к определенному пределу погрешность сходящегося алгоритма стремится к нулю. Таким образом, значение погрешности численного метода можно регулировать, а выбирать

29

ее целесообразно в 2–5 раз меньшей неустранимой погрешности. Если сходимость метода доказана, то представление о его точности дает сопоставление расчетов, выполненных при различных значениях параметра численного метода.

Для проверки вычислительного алгоритма широко используется также система тестов. Тестом служит задача, содержащая специфические трудности данного класса задач, с известным точным ее решением.

Контрольные вопросы

1.Перечислите этапы численного эксперимента.

2.Какие факторы должны учитываться при разработке численного метода?

3.Назовите и поясните источники погрешностей численного эксперимента.

30