НИРС Андреев / МНИ

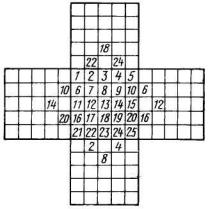
и пяти уровней

Производя такое усреднение для каждого уровня фактора х1 можно найти зависимость результата только от этого фактора при нейтрализации влияния остальных трех факторов. Аналогично можно выявить влияние только фактора х2 при нейтрализации х1, х3 и х4 . Меняя порядок усреднения, можно из одних и тех же данных 25 опытов найти влияние всех четырех первичных факторов. Таким образом, данная методика позволяет заменить полное число сочетаний влияющих факторов, равное 625, всего лишь 25 специально подобранными сочетаниями факторов, т.е. сократить объем экспериментов в 25 раз.

Методика построения комбинационных квадратов. Весь после-

дующий анализ проводится для четырех первичных независимых друг от друга факторов. При этом решение более простых случаев зависимости результатов от трех или двух факторов может быть получено из основного случая при условии, что один или два фактора будут постоянными.

Строится большой комбинационный квадрат (рис. 8.2) и рядом помещается средний квадрат в окружении четырех таких же средних квадратов, примыкающих к нему крест-накрест (см. верхнюю часть рис. 8.2). Пронумеруем в среднем квадрате все клетки от 1 до 25. Центральную клетку в большом квадрате обозначим цифрой 13, т.е. цифрой, располагающейся в центральной клетке среднего квадрата. Затем отметим клетки отдельного среднего квадрата, идущие по диагонали слева направо и сверху вниз 1, 7, 13, 19, 25, и аналогичные им клетки в третьем столбце большого квадрата просто сверху вниз. Отметим также клетки отдельного среднего квадрата, идущие сверху вниз и справа налево, 5, 9, 13, 17, 21 и аналогичные им клетки в третьей строке большого квадрата, идущие справа налево. Таким образом, клетки, располагающиеся на диагонали отдельного среднего квадрата 1, 7, 13, 19, 25, расположатся на большом квадрате вдоль крутой наклонной линии в третьем столбце. Клетки, располагающиеся вдоль другой диагонали 5, 9, 13, 17, 21, при переносе со среднего квадрата на большой квадрат расположатся полого в третьей строке большого квадрата.

81

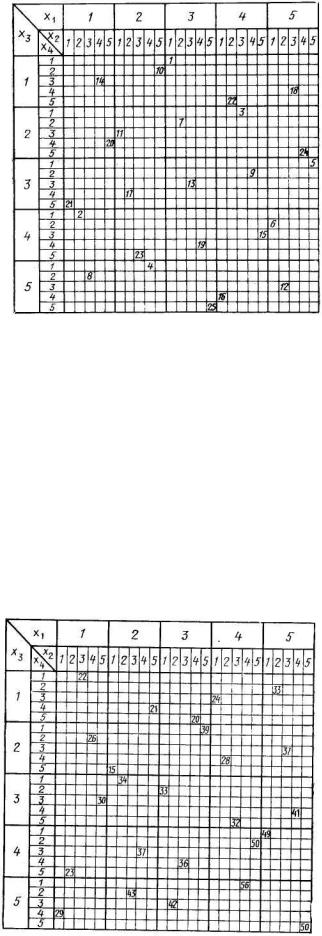
Рис. 8.2. Схема построения большого комбинационного квадрата

Если использовать этот же прием, но отсчет вести не от центральной клетки 13, а от какой-либо другой, например 19, то придется продолжить диагональ в квадраты, примыкающие к отдельному среднему квадрату, т.е. взять клетки 2, 23, 19, 15, 6. При переносе этих клеток в большой квадрат они расположатся вдоль ломаной линии в четвертой строке большого квадрата. Продолжая это построение, получаем расположение всех 25 клеток в большом комбинационном квадрате, причем все клетки будут иметь различные номера, т.е. соответствовать различным сочетаниям первичных факторов.

Аналогичными приемами могут быть построены комбинационные квадраты для 7-го, 8-го и т.д. уровней каждого из четырех факторов.

82

Рис.8.3 Заполненный комбинационный квадрат

Методика обработки данных. Сущность методики рассмотрим на примере для четырех факторов х1, х2, х3, х4, каждый из которых может принимать одно из пяти следующих значений: 1, 2, 3, 4, 5. Опыты выполнены по плану, изображенному на рис. 8.3. В клетках, обозначающих комбинации уровней факторов в опытах, записаны значения переменной величины у, полученные в результате проведения эксперимента. Данные опытов сгруппируем по значениям факторов (табл. 8.1, 8.2).

						Таблица 8.1
х2			х1			Среднее
	1	2	3	4	5
1	29	15	33	24	49	30
2	23	34	42	28	33	32
3	22	43	36	32	37	34
4	26	37	20	56	41	36
5	30	21	39	50	50	38
среднее	26	30	34	38	42	–

Для каждого уровня первого, второго, третьего и четвертого факторов находим средние значения величины у. Нанося в системе координат средние значения величины у, соответствующие уровням фактора х1, получаем график зависимости у от х1. Аналогично строятся графики зависимостей у от остальных факторов. Согласно полученным данным функция у линейно зависит от каждого из факторов. Параметры этих зависимостей найдем с использованием метода наименьших квадратов. Так как все графики частных зависимостей величины у от каждого из факторов аппроксимируются с достаточной точностью прямыми, то зависимость у от всех факторов может быть представлена суммой частных зависимостей.

						Таблица 8.2
х4			х3			среднее
	1	2	3	4	5
1	22	39	34	49	56	40
2	33	26	33	50	43	37
3	24	37	30	37	42	34
4	21	28	41	36	29	31
5	20	15	32	23	50	28
среднее	24	29	34	39	44	–

Свободный член этой зависимости b0 определяется следующим образом. Подставляя в найденное уравнение значения факторов первого опыта и величину у1, полученную в этом опыте, находим значение b01. Аналогично

83

находим для последующих опытов величины b02, b03,…, b0k. Искомый пара-

метр b0 определяем как среднеарифметическое величин b01, b02,…, b0k, где k

– число проведенных опытов.

Таким образом, методика рационального планирования эксперимента, существенно уменьшая число необходимых опытов, позволяет исследовать некоторые многофакторные системы, однако она имеет и ряд недостатков. К числу основных недостатков относятся: отсутствие статистического обоснования результатов, что может привести к ошибочным выводам; ограниченная область применения (описанная методика построения плана эксперимента пригодна не для всякого числа уровней факторов); несовершенство и недостаточная обоснованность способа получения эмпирических зависимостей.

Эти недостатки устраняются в методах статистического планирования эксперимента.

8.3. Планирование первого порядка

Представление неизвестной функции отклика (8.1) полиномом является наиболее удобным. На первой стадии исследования обычно принимают полином первой степени. Так для трехфакторной задачи теоретическое уравнение регрессии в этом случае имеет вид

3	3
M {y}= b0 + åbi xi +	åbiu xi xu + b123 x1x 2 x3 .	(8.2)
i=1	i,u=1
	i<u

Уравнение регрессии, получаемое на основании результатов эксперимента, в отличие от приведенного выше теоретического уравнения, имеет вид

3	3
y = b0 + åbi xi +	åbiu xi xu + b123 x1x2 x3 ,	(8.3)
i=1	i,u=1
	i<u

где коэффициенты регрессии b0 , bi , biu , b123 являются оценками для теоре-

тических коэффициентов регрессииb0 , bi , biu , b123 , т.е.

bi ® bi ; biu ® biu ; b123 ® b123 ; b0 ® b0 .

Выбор основных факторов и их уровней. В качестве факторов можно выбирать только контролируемые и управляемые переменные, т.е. такие, которые исследователь может поддерживать постоянными в течение каждого опыта на заданных уровнях. В число факторов должны быть включены параметры процесса, оказывающие наиболее сильное влияние на функцию отклика. Для выяснения наиболее важных факторов анализируется априорная информация, ранее проведенные аналитические и экспериментальные исследования. При необходимости с этой целью проводят специальные опыты, получившие название «отсеивающий эксперимент».

84

Для каждого фактора надо указать тот интервал изменения параметров, в пределах которого ставится исследование. Для этого на основе априорной информации устанавливаются ориентировочные значения факторов (при оптимизации они выбираются так, чтобы их комбинации давали наилучший результат или близкий к нему). Этой комбинации значений факторов соответствует многомерная точка в факторном пространстве, которая и принимается за исходную точку при построении плана эксперимента. Координаты этой точки называют основными (нулевыми) уровнями факторов.

Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний уровни фактора. Этот интервал принимается за единицу нового масштаба измерения фактора. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний – 1, а основной соответствовал 0.

Для факторов с непрерывной областью определения это достигается с помощью формулы преобразования

		~	~	~	(8.4)
		xi = (xi - xi0 )/ Dxi ,
где xi– кодированное значение фактора;			~	– значение фактора в натуральных
			xi
единицах;	~	– значение основного уровня в натуральных единицах;			~
	xi0				Dxi –

единица масштаба (интервал варьирования); i – номер фактора.

Выбор интервалов варьирования производится на основе опыта и интуиции исследователя. При этом следует учитывать точность фиксирования факторов, оценивать силу влияния фактора на отклик у, погрешность измерения величины у. Все это поможет избежать ситуации, при которой интервал варьирования окажется недостаточным для того, чтобыВажноуловитьучитыватьзменениехарактеру. решаемой задачи. При решении: задачи оптимизации стремятся выбрать для первой серии экспериментов такую единицу масштаба, которая давала бы возможность для шагового движения к оптимуму. При описании процесса единица масштаба должна охватывать всю область, подлежащую описанию интерполяционным полиномом.

Минимально необходимое число уровней факторов на единицу больше порядка интерполяционного полинома. Поскольку результаты наблюдений отклика носят случайный характер, приходится в каждой точке плана проводить m параллельных опытов (обычно m = 2 ÷ 4), осреднение результатов которых дает возможность уменьшить погрешность оценки истинного значения

отклика в m раз. Эксперимент делится на m серий опытов. В каждой серии последовательность опытов рандомизируется, т.е. с помощью таблицы случайных чисел определяется случайная последовательность реализации опытов в каждой серии. Рандомизация: позволяет ослабить или исключить вовсе влияние неконтролируемых случайных или систематических погрешностей на результаты исследования.

Полный факторный эксперимент (ПФЭ). Полным факторным экс-

периментом называется эксперимент, реализующий все воз-

85

можные неповторяющиеся комбинации уровней независимых факторов, каждый из которых варьируется на двух уровнях. Число этих комбинаций равно 2N. Нахождение уравнения регрессии методом ПФЭ состоит из: а) планирования эксперимента; б) собственно эксперимента; в) проверки воспроизводимости (однородности выборочных дисперсий); г) получения уравнения регрессии с проверкой статистической значимости коэффициентов регрессии; д) проверки адекватности уравнения регрессии.

									Таблица 8.3
№ точки	x0	x1	x2	x3	x1x2	x1x3	x2 x3	x1x2 x	Отклик
плана (v)
1	+1	-1	-1	-1	+1	+1	+1	-1	у1
2	+1	+1	-1	-1	-1	-1	+1	+1	у2
3	+1	-1	+1	-1	-1	+1	-1	+1	у3
4	+1	+1	+1	-1	+1	-1	-1	-1	у4
5	+1	-1	-1	+1	+1	-1	-1	+1	у5
6	+1	+1	-1	+1	-1	+1	-1	-1	у6
7	+1	-1	+1	+1	-1	-1	+1	-1	у7
8	+1	+1	+1	+1	+1	+1	+1	+1	у8

Условия эксперимента записывают в виде матрицы планирования. Пример матрицы планирования для трех факторов дан в табл. 8.3. Здесь столбцы х1, х2, х3 образуют матрицу плана. Эти столбцы задают планирование – по ним определяются условия опытов. Последующие столбцы матрицы получаются перемножением соответствующих значений факторов х1, х2, х3. В матрицу добавляется еще один столбец – фиктивная переменная х0 для расчета свободного члена b0 в уравнении регрессии. Значение х0 одинаково во всех строчках и равно +1.

Матрицу плана можно представить геометрически (рис. 8.4). Условия проведения опытов соответствуют координатам вершин куба, центром которого является основной уровень, а ребра соответственно параллельны координатным осям, их длина равна. двум интервалам. Номера вершин куба соответствуют номерам точек в матрице планирования.

86

Рис. 8.4. Геометрическое изображение полного факторного эксперимента 23

Можно наглядно показать, что точность определения уравнения регрессии с использованием методов ПЭ выше. Иллюстрируем сказанное примером. Пусть требуется найти коэффициенты регрессии b0 и b1 уравнения y = b0 + b1x по двум опытам. При одинаковых погрешностях с увеличением интервала или радиуса области изменения фактора х точность определения коэффициентов регрессии растет. Перенесем этот принцип повышения точности линейного уравнения регрессии на многофакторные процессы. Это можно сделать двумя путями. Первый путь – увеличение интервалов варьирования по каждому фактору (точно так же, как и в однофакторном процессе). Однако в многофакторном пространстве есть еще один принципиально иной путь увеличения радиуса области изменения факторов – путь одновременного варьирования уровней всех факторов без увеличения интервала каждого фактора. Рассмотрим, что это дает при N = 2 (при –1, +1). Опыты, спланированные по методике однофакторного эксперимента, в факторном пространстве, очевидно, будут представлены точками (0, +1), (0, –1), ( + 1, 0), (–1, 0) (рис. 8.5), лежащими на осях x1 и x2.

Если же изменить значения уровней факторов одновременно,, то точки плана, построенного в соответствии с концепцией многофакторного эксперимента, расположатся в вершинах внешнего квадрата (+1, +1), (–1, +1), (–1, –1), (+1, –1) (рис. 8.5). Ясно, что при этом исследованная область изменения факторов будет больше. Отметим, что этот эффект тем ощутимее, чем больше размерность N факторного пространства. В самом деле, при планировании по методике однофакторного эксперимента опорные точки всегда располагаются на концах хорд длиной 2 единицы, при многофакторном планировании опорные точки располагаются на концах диаметров, длина которых

2 N 2 , т. е. в N раз больше.

При N = 2 построение матриц ПФЭ не вызывает затруднений, при увеличении же числа факторов возникает необходимость в некоторых специальных приемах построения матриц. Рассмотрим два наиболее простых приема. Первый прием основан на правиле чередования знаков. В первом столбце знаки чередуются поочередно, во втором – через 2, в третьем – через 4, в четвертом – через 8, в пятом – через 16 и т.д. по степеням двойки. Второй прием

87

основан на последовательном достраивании матрицы. Для этого при добавлении нового фактора необходимо повторить комбинации уровней исходного плана сначала при значении нового фактора на верхнем уровне, а затем – на нижнем.

Матрицы ПФЭ обладают рядом свойств, делающих их оптимальным средством получения уравнения регрессии по результатам эксперимента. Для любого числа факторов коэффициенты будут вычисляться по формуле

			1		k
	bi =				å xiv				v ,	(8.5)
								y
			k v =1
						1	m
	где i = 0, 1, 2,.., N – номер фактора;			v =			å yv j			- средний отклик по m опы-
		y
						m j=1

там в точке с номером v (здесь j – номер параллельного опыта в точке v); k – число опытов в матрице.

Планирование эксперимента исходит из статистического характера зависимостей, поэтому полученные уравнения связи подвергаются тщательному статистическому анализу с целью извлечь из результатов эксперимента максимум информации и убедиться в достоверности полученной зависимости и ее точности.

Каждый эксперимент несет в себе какую-то погрешность, для повышения надежности производят повторения опытов при тех же условиях, т.е. повторяют для каждой строки таблицы планирования.

Построчные дисперсии подсчитывают по формуле

		åm (yvj -		v )2
			y
	sv2 =	j=1			,	(8.6)
		m -1

где m – число повторных опытов в точках плана.

Дисперсия отклика s2{y} есть среднеарифметическая дисперсий всех k различных вариантов опытов:

	k		k m	2
	å sv2		å å(yvj - yv )
s 2 {y}=	v=1	=	v=1 j=1		.	(8.7)
	k		k(m -1)

Прежде чем производить объединение дисперсий, надо убедиться в их однородности. Проверка производится с помощью критериев Фишера и Кохрэна. Гипотеза об однородности дисперсий принимается, если экспериментальное значение критерия Кохрэна или Фишера не превышает табличного значения.

Далее на основе метода наименьших квадратов находится уравнение регрессии, после чего предстоит выполнить статистические оценки полученного уравнения.

88

Проверка значимости каждого коэффициента проводится независимо. Для этого можно использовать проверку по t-критерию Стьюдента. Прежде всего, находят дисперсию коэффициента регрессии. При равномерном дублировании опытов по точкам с числом повторных опытов т она определяется по формуле

s2{b }=	s2	{y}		(8.8)
			.
i	km

Далее рассчитываются значения ti-критерия. Если ti>tкр, то коэффициент bi признается значимым, в противном случае bi считается статистически незначимым, т.е. bi = 0. После этого уравнение регрессии составляется в виде

уравнения связи выходного параметра у и переменных хi , включающего только значимые коэффициенты.

После вычисления коэффициентов уравнения следует прежде всего проверить его пригодность или адекватность. Для этого достаточно оценить отклонение выходной величины у, предсказанной уравнением регрессии, от результатов эксперимента у в различных точках факторного пространства.

Рассеяние результатов эксперимента относительно уравнения связи, аппроксимирующего искомую функциональную зависимость, можно охарактеризовать с помощью остаточной дисперсии или дисперсии адекватности

sад2 , оценка которой, справедливая при равном числе дублирующих опытов, находится по формуле

		sад2 =			m		åk (			v -yˆ v )2 ,	(8.9)
									y
				k
					- r v=1
где r – число членов аппроксимирующего полинома.
Проверка адекватности состоит в выяснении соотношения между дис-
персией адекватности s2			и дисперсией воспроизводимости s2{y} и прово-
	ад
дится с использованием критерия Фишера F, который в данном случае фор-
мируется как отношение			F = s 2			/ s 2		{y}.Если вычисленное значение крите-
				ад
рия меньше	критического Fкр					для		соответствующих			степеней свободы
f ад = k - r и	f E = k(m -1)при заданном уровне значимости a, то описание

признается адекватным объекту.

Рассмотрим пример использования полного факторного эксперимента. Уравнение подобия, описывающее теплоотдачу на дне прямоугольной полости, которая расположена поперек основного потока, при организации перед ней струйной завесы, полностью изолирующей полость от основного течения, можно представить в виде

		~		~	~			~
St			Re	b1		b	2	b	(8.10)
	s	= b		s	H			- z 3 ,
		0

89

где Sts, Res – числа Стантона и Рейнольдса, построенные по параметрам струн и длине полости L; H = H / L – относительная глубина полости; ~z = z / L – относительная координата вдоль дна полости.

~ ~ ~ ~

Коэффициенты b0 , b1, b2 и b3 найдем методом планирования эксперимента. Прологарифмировав (8.10), получим линейное уравнение регрессии,

где в качестве факторов служат	~	~	~	и	~	~	. Запишем
	x1	= ln Re s ; x2	= ln H		x3	= ln z

его в кодированных значениях факторов хi (8.4), учтем также их возможное взаимное влияние:

		3			3
	y = b0 + åbi xi			+	åbiu xi xu			+ b123 x1 x2 x3 .			(8.11)
		i=1			i,u=1
					i<u
Здесь y = ln St s ; bi		~	~			~	3	~ ~
		= bi Dxi ; b0			= ln b0 +		åbi xio .
~							i-1
Уровни факторов		xi и интервалы их варьирования представлены в табл.
8.4.
											Таблица 8.4
	Уровни факторов							Факторы
						~			~	~
						x1			x2	x3
	Основной 0					16,242			-0,634	-1,007 -
	Верхний +1					16,545			0,1823 -	0,1727 -
	Нижний -1			~		15,9387			1,4503	1,8413
						0,303			0,8163	0,8343
	Интервал варьирования Dxi

Для нахождения коэффициентов уравнения (8.11) проведем ПФЭ с числом опытов 23. Опыты будем выполнять согласно матрице плана, приведенной в табл. 8.3, в случайной последовательности, а в каждой точке плана повторим их 3 раза. Далее вычислим построчные дисперсии (8.6), проверим их однородность по критерию Кохрэна и определим дисперсию отклика (8.7). Коэффициенты уравнения (8.11) вычисляются по формуле (8.5), после чего по выражению (8.8) находятся их дисперсии и по критерию Стьюдента проверяется значимость каждого коэффициента.

Обработка 24 опытов (8 опытов в матрице плана, повторенные 3 раза), проведенных на воздухе, позволила вычислить коэффициенты регрессии и после потенцирования уравнения (8.11) привести его к виду (полученное уравнение записано в натуральных значениях факторов и с учетом лишь значимых коэффициентов)

	-0,927		(12,847-0,817 ln Res -0,165 ln		)
				z		- z	0,458		(8.12)
		H						.
	Sts =1224,9 Res

90