НИРС Андреев / МНИ

	1	l
Rx*(lD) =		å[x(ti ) - m*x ][x(ti + l )- m*x ]; l = 1, 2, 3 .....				(9.7)
	n - l -1 i=1
Оценка дисперсии вычисляется при l– 0:
	D x*	=		1	ål [x (t i )- m *x ]2	(9.8)
			n
				- 1 i =1

Спектральная плотность может быть определена как преобразование Фурье корреляционной функции, так и с помощью набора узкополосных фильтров и вычисления средних квадратичных значений выходных величин этих фильтров.

Чтобы статистические характеристики обладали требуемой точностью, необходимо правильно спланировать эксперимент по получению исходной реализации. В данном случае это означает правильный выбор длины реализации Т и частоты съема точек этой реализации.

Количественная мера зависимости точности оценки от длины реализации может быть получена в общем виде лишь при априорном знании корреляционной функции процесса. В то же время на практике необходимо заранее, до вычисления оценок корреляционных функций, уметь хотя бы приближенно оценивать параметры реализации, позволяющие получать требуемую точность. Существуют различные рекомендации. Остановимся на одной из методик приближенного определения длины реализации и частоты съема точек.

Рассматривается класс монотонно убывающих корреляционных функций, которые с достаточной точностью могут быть представлены выражением:

Rx (q) = R(0)exp(- a		q		),	(9.9)

где a, R(0) – неизвестные параметры.

При этом относительная погрешность определения ординат корреляционной функции, которая представляет собой отношение дисперсий этих ординат к их средним значениям, может быть приближенно определена по формуле:

	D	R	(q)		é	æ at			öù
e(q) =					= êc + 0,01ç			0	÷ú[exp (paq)+ exp (- 0,9aq)], (9.10)
	Rx		(q)
					ë	è	2		øû

где с и р – функции aТ, показанные на рис. 9.1; t0 – расстояние между соседними точками съема по реализации процесса.

111

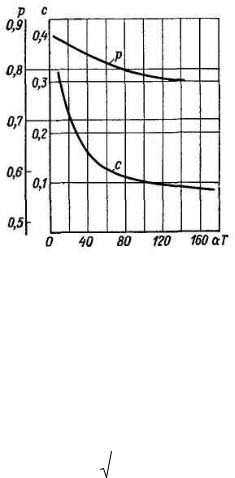
Рис. 9.1. Графики зависимостей с и р от aТ

Известно, что значение параметра аппроксимации корреляционной функции может быть непосредственно оценено по реализации процесса. Для этого следует воспользоваться формулой, связывающей среднее число нулей в единицу времени (среднее число пересечений реализации процесса его математического ожидания в единицу времени) с показателем a

			1
	n	=			1,5a2 = 0,39a.		(9.11)
			p
	0

Вообще говоря, эта формула справедлива только для дифференцируемого случайного процесса, для которого число пересечений конечно. Так как наблюдения над реальными процессами ведутся на выходе объектов, которые отличаются большой инерционностью, то это условие, как правило, выполняется.

Непосредственная достаточно хорошая оценка значения п0 может быть получена во многих случаях по сравнительно небольшой длине реализации.

Подсчитывается по реализации процесса среднее число нулей в единицу времени п0 и по формуле (9.11) рассчитывается a. В требуемой точке корреляционной функции задаются значением ε(θ) и по формуле (9.10) определяют искомые значения параметров реализации Т и t0. После того, как получены корреляционные функции, в ряде случаев возникает необходимость их аппроксимации аналитическими выражениями. Эта задача по существу не отличается от аппроксимации любых функций. Необходимо только, чтобы выбранная аппроксимация отражала существенные свойства исследуемого процесса и была удобной для дальнейших исследований.

Качество аппроксимации оценивается средним модулем I1 или средним квадратом I2 отклонения аналитической кривой от экспериментальной:

112

I1 =	1	ån [R x (i )- R x* (i )];
	n
		i =1		(9.2)
		1	n	2

=n - 1 i =1

9.2.Методы определения статических и динамических характеристик объекта при пассивном экспериментеR x (i )][R (i )- .I 2 å

Определение характеристик объектов по данным экспериментальных исследований называется идентификацией. Идентификация означает отождествление модели объекту – оригиналу.

Если характеристику объекта представляет оператор At, который ставит в соответствие произвольному входному сигналу x(t) выходной сигнал y(t)

y(t) = At{x(t)},

(9.13)

то задача идентификации заключается в определении некоторой оценки А*,

которая используется в качестве характеристики оператора At. При этом случайный процесс на выходе модели есть:

y*(t)= Аt{x(t)}

(9.14)

Очевидно, говорить о соответствии между моделью и объектоморигиналом можно только в том случае, если оценка оператора А* близка в некотором смысле его истинному значению, Требование близости оператора

At и его оценки А* означает, что при этом должны выполняться требования близости случайной функции на выходе модели y*(t) случайной функции на выходе объекта y(t). Структурная схема задачи идентификации показана на рис. 9.2.

Рис. 9.2. Структурная схема задачи идентификации.

Критерием близости в зависимости от постановки задачи могут служить различные показатели. При идентификации объектов управления технологических процессов и производств в большинстве практически случаев

113

оценки операторов ищутся по критерию минимума средней квадратичной ошибки.

В соответствии с общей методикой для решения задачи идентификации необходимо располагать определенным статистическим материалом. Этот материал может быть накоплен с помощью пассивного или активного эксперимента.

Пассивный эксперимент основан на регистрации контролируемых переменных в режиме нормальной эксплуатации объекта без внесения какихлибо преднамеренных возмущений. В активном эксперименте искусственные возмущения вводятся в объект по заранее спланированной программе.

Каждый способ имеет свои области применения. Пассивный эксперимент обычно применяется при анализе каналов прохождения возмущений и исследований связи между контролируемыми переменными в производственных условиях, активный – при исследовании каналов передачи управляющих воздействий промышленных объектов, а также когда процесс исследуется на лабораторной или полупромышленной установке. В последних случаях экспериментатор имеет возможность целенаправленно и эффективно раскрывать зависимости между переменными и определять области оптимальных значений режимов.

Основным этапом идентификации является обработка экспериментальных данных и определение оценок искомых операторов. Для решения этой задачи используется аппарат математической статистики (регрессионный и дисперсионный анализ), а также статистической динамики. Применение того или иного аппарата в основном определяется видом искомой модели.

При описании процессов выделяются два типа моделей. Первый определяет связь различных переменных в статическом режиме. В основе этих моделей лежат уравнения статики. Второй тип моделей определяет связь различных переменных в динамическом режиме. В их основе лежат дифференциальные уравнения, весовые функции или частотные характеристики, описывающие поведение объекта при различных формах воздействий.

9.2.1. Определение статических моделей по данным пассивного эксперимента

Статические модели объектов представляют собой функциональные зависимости между входными и выходными переменными, которые характеризуют установившийся режим работы агрегата. В этом режиме входные и выходные переменные с определенной степенью точности постоянны во времени, а их производные, входящие в уравнения связи, равны нулю.

Зависимости между переменными могут изучаться по экспериментальным данным, как содержащим всю необходимую информацию об их связи, так и полученным на фоне действия неконтролируемых (мешающих) факторов. Не рассматривая первый случай, для которого существуют специальные регулярные методы определения зависимостей, остановимся на втором более общем случае, требующем привлечения статистических методов..

114

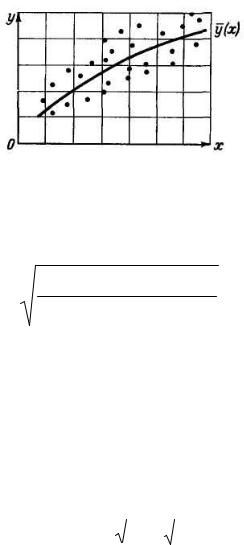
При определении статических моделей статистическими методами задача сводится к поиску неслучайных характеристик связи, устанавливающих функциональные зависимости между переменными. Эти зависимости называют уравнениями регрессии. Уравнение регрессии представляет собой зависимость условного математического ожидания некоторой величины у от фиксированных значений х (рис. 9.3):

М{у/х}=у(х)

(9.15)

Показателями степени связи между случайными величинами х и у служат корреляционное отношение hху или коэффициент корреляции rху.

Рис. 9.3. Линия регрессий.

Корреляционное или, как его иногда называют, дисперсионное отношение определяется как

	h xy =	M {[(y / x ) - m y ]2	}.	(9.16)
		M {[y - m y ]2 }

Корреляционное отношение устанавливает долю, которую вносит изменчивость величины х в общую дисперсию величины у.

В том случае, когда связь является чисто функциональной, η = 1. Во

всех остальных случаях стохастической связи 0 < ηху< 1 Частным случаем корреляционного отношения при линейной форме

связи является коэффициент корреляции rху. Он определяется как
r	= b*			/			,	(9.17)
		D	x		D	y
xy

где Dx – дисперсия случайного процесса х; Dy – дисперсия процесса у, b* – коэффициент пропорциональности, смысл которого будет определен далее.

Коэффициент корреляции может быть определен по формуле:

115

r =	M ((x - mx )( y - m y )			=		Rxy (0)
								(9.18)
xy		Dy Dx				Rx (0)R y (0)

На практике во многих случаях следует ожидать, что если корреляционная связь имеется, то она скорее всего является прямолинейной. Гипотеза о линейной форме связи проверяется с помощью F-критерия (критерия Фишера)

F = k	2	(h2	- r 2 ) / k (1 - h2		)	(9.19)
		xy	1	xy

имеющего F-распределение с k1 и k2 степенями свободы. Напомним, что под числом степеней свободы понимается разность между количеством независимых измерений и числом констант найденных по этим измерениям. Прав-

доподобность гипотезы оценивается по вероятности P(F > Fq) = a/2, где Fq – граница распределения, соответствующая заданному уровню значимости (значению вероятности, отвечающему событиям, которые можно считать невозможными). В математической статистике составляются таблицы значений

Fq, зависимых от чисел степеней свободы и уровня значимости а. Если в ре-

зультате оценки оказывается, что F < Fq, то гипотеза о линейной форме связи принимается.

Построение математических моделей объектов по экспериментальным данным в виде уравнений регрессии является типичной задачей аппроксимации. В простейшем случае линейной связи двух переменных уравнение регрессии представляется зависимостью:

у = а+bх. (9.20)

Если выходная переменная является линейной функцией многих пере-

менных х1, ..., хт, уравнение регрессии можно представить в следующем виде:

m
y0 = a0 + a1x1 + ... + am xm = åai xi .	(9.21)

i=1

Если зависимость между переменными имеет более сложный характер, то для ее описания может потребоваться более сложная модель, например квадратичная:

m	m	c2
y = a0 + åai xi + åai x 2j		m
		+ åaij xi x j	(9.22)
i=1	ij	ij=1

116

где С2 – число сочетаний из т элементов по два.

Используя функциональное преобразование переменных, выражение (9.22) можно свести к линейному виду. Для этого положим xj.=zj; xixj=zk; aij=ak. Тогда

m	m	c2
		m
y = a0 åai xi + åa j x j + åak xk .			(9.23)
i=1	j=1	k =1

В общем случае зависимость между переменными может быть с учетом указанных преобразований представлена в виде линейного уравнения:

y = åai xi .

(9.24)

Понятно, что в общем случае неизвестными могут быть как число членов полинома (структура модели), так и коэффициенты при переменных. Определение этих неизвестных является задачей регрессионного анализа.

При решении этой задачи вначале положим, что структура модели известна и по выборке экспериментальных данных необходимо определить оценки коэффициентов.

Для оценки коэффициентов воспользуемся методом наименьших квадратов. В соответствии с этим методом оценки коэффициентов определяются из условия:

	n
min I = y(a1,..., am ) = å( yi - yi* )2 .		(9.25)
ai	i =1

где yi – значение выходной переменной по данным наблюдений; y*i – соответствующее значение выходной переменной, предсказанное с помощью регрессионной модели.

Для получения оценок a1,…, am при которых значение функции I минимально, применяются обычные методы математического анализа. Условием минимума является dI/daj = 0 (I = 1, 2, ..., т).

Рассмотрим вначале случай оценки в линейной модели (9.20). Здесь искомыми являются а и b.

Функция ошибки для такой модели будет определяться соотношением:

n
I (a,b) = å( yi - a - bxi )2 .	(9.26)

i =1

117

Дифференцируя (9.26) вначале по а, а затем по b и приравнивая результаты дифференцирования нулю (условие экстремума), получим:

	dI (a, b)	n
		= -å( yi - a - bxi ) = 0;
	da
		i=1	(9.27)
	dI (a, b)	n
		= -å( yi - a - bxi )xi = 0.
	db
		i=1

Отсюда, опуская несложные преобразования, запишем систему так называемых нормальных уравнений:

	n	n
	an + b å xi = å yi ;
	i=1	i=1		(9.28)
	n	n	n
	a å xi + b å xi2		= å xi yi .
	i=1	i=1	i=1

Решая ее, получим:

		n n		n	n
		å yi å xi2 - å xi å xi yi
a =		i=1 i=1		i=1 i=1			;
		n
					n
		n å xi2 - ( å xi )
		i=1		i=1			(9.29)
		n		n	n
		n å xi yi - å xi å yi
b =	i=1		i=1 i=1			.
		n	æ	n	ö2
		n å xi2 -	çç	å xi ÷÷
		i=1	èi=1		ø

Найденные значения а и b носят смысл оценок коэффициентов регрессии. Выполнив преобразование над (9.29), можно показать, что

a = m*y - bm*x ;
b = r *			..	(9.30)
	D*	/ D*
xy	y	x

Здесь r*yх, mу*, m*x, D*у, D*x – оценки коэффициента корреляции, математических ожиданий и дисперсии величин х и у.

118

Полученные результаты легко распространить на случай модели со многими переменными, где все коэффициенты для единообразия обозначены

через аi. Мерой тесноты связи для случая многих переменных служит коэффициент множественной корреляции rx1...xm . Этот коэффициент может быть

определен через коэффициенты парной корреляции переменных, участвующих в уравнениях. Например, для уравнения с двумя переменными х1 и х2 коэффициент множественный корреляции определяется по формуле:

rx x	2	y =	(r 2	+ r 2		y	+ 2rx x	2	) /(1 - r 2	).		(9.31)
1			x y	x	2		1		х х	2
			1						1

С целью упрощения вычислений и уменьшения погрешностей переменные многомерных моделей принято представлять в стандартизованном виде:

y0

= ( y - m

)

; x0

= (x - m

.

(9.32)

y

D

y

xj

) / D

xj

t

i

ji

ij

Функция ошибки для случая модели со многими переменными будет равна:

n	- a2 x20i .....am xmi0 ) .
I (a1,..., am ) = å( yI0 - a1x10i		(9.33)
i =1

Минимизируя это выражение, положим:

dY	=	dY	= ..... =	dY	= 0 .	(9.34)
		da2
da1				dam

Пользуясь условием (9.34), получим систему нормальных уравнений, выраженную через коэффициенты парной корреляции стандартизованных переменных, которая в матричной форме может быть записана в виде:

А×а=с ;

или

	1	rx1x2	. rx1xm				a1			rx1y
A =	rx2 x1	1	.	rx1xm	;	a =	a2	;	c =	rx1y	.	(9.35)
	.	.	.	.			.			.
	rxm x2	rxm x2	.	1			am			rx1y

Коэффициенты парной корреляции между стандартизованными переменными определяются формулами:

119

			1	n
	rx j xl	=		åx0ji xli0 ; rx j y
			n l =1

		1	n
	=		åx0ji yi0 .	(9.36)
		n i =1

В результате решения системы (9.35) определяются коэффициенты стандартизованного уравнения:

а = сА-1.

(9.37)

При составлении системы (9.35) иногда необходимо количественно проверять гипотезу о существовании связи между переменными, т.е. не объясняются ли полученные значения rx j xl случайностями выборки. Для этого

пользуются вспомогательной величиной

t = rx j xl

(n - 2)(1 - rx j xl )

(9.38)

распределенной по закону Стьюдента с п – 2 степенями свободы. Данные распределения и граничные значения tq в зависимости от степени свободы и уровня значимости приведены в книгах по математической статистике. Гипо-

теза принимается, если t > tq.

До сих пор предполагалось, что структура модели известна. В действительности структура априори, как правило, неизвестна. Поэтому при изучении процесса последовательно задаются моделями разной структуры и оценивают их адекватность процессу. Показателем степени адекватности исследуемой модели принято считать величину остаточной дисперсии.

В литературе по регрессионному анализу величины остаточной дисперсии обозначаются S2 и вычисляются как

		1	n
	S 2 =		å( yi - yi*)2 .	(9.39)
		n - k -1i =1

где п – число измерений; k – число независимых друг от друга констант, найденных по этим измерениям. В совокупности (n– k – 1) представляют число степеней свободы остаточной дисперсии.

Можно указать, по крайней мере, две причины, по которым модель может быть неадекватной. Во-первых, могут существовать некоторые неучтенные факторы, влияющие на выходную переменную у. Тогда модель может быть улучшена за счет их включения. Во-вторых, может сказаться погреш-

ность измерения переменных yi и xi. Тогда для улучшения модели необходимо повторить эксперименты или увеличить их число.

Так как величины остаточных дисперсий S2 оцениваются по конечному числу экспериментальных данных, то они сами являются случайными. По-

120