НИРС Андреев / МНИ

Рекомендуется следующий порядок построения линейных графиков:

а) полученные данные наносят на график с координатами х, у и проводят плавную кривую;

б) из табл. 7.1 выбирают функцию, характер изменения которой в наибольшей степени совпадает с характером изменения опытной кривой;

в) преобразование осей координат производят в соответствии с указаниями табл. 7.1.

В новой системе координат получается линейная зависимость, которую можно использовать для дальнейшего анализа.

В координатах ξ, η функция, аппроксимирующая опытные данные, принимает вид

h = a1 + a2x

(7.8)

В этом случае система уравнений (7.1) или (7.3) для определения сво-

бодных параметров а1 и а2 включает два уравнения и легко решается.

Расчетные формулы для определения параметров а1 и а2

методом наи-

меньших квадратов имеют вид

N

N

N

N

N

N

N

åxi åxi hi

- åhi åxi2

åxi

åhi

- N åxihi

a =

i =1

i =1

i =1

i =1

; a

2

=

i =1

i =1

i =1

.

(7.9)

1

æ

N

ö2

N

æ

N

ö2

N

çç

åxi ÷÷

- N åxi2

çç

åxi

÷÷

- N åxi2

èi =1 ø

i =1

èi =1

ø

i =1

Значения величин ξi, ηi

находят по результатам эксперимента. Пара-

метр а1 определяет длину отрезка, отсекаемого аппроксимирующей прямой на координатной оси η, построенной от начала координат, а параметр а2 характеризует угол наклона этой прямой к координатной оси ξ. Значение а2 численно равно тангенсу этого угла (рис. 7.3). Иногда значение одного из свободных параметров (а1 или а2) удается определить из теоретических соображений. В этом случае один из параметров фиксируется, а другой свободный параметр находится с помощью полученных опытных данных методом наименьших квадратов. Расчетные соотношения метода наименьших квадратов:

Рис. 5.3. Нахождение аппроксимирующей функции с предварительным преобразованием системы координат

71

а) известно значение a1,

			N
			åhi	- a1N
a2	=		i =1		;		(7.10)
			N
			åxi
			i =1
б) известно значение а2,
			N	N
		åhi		- a2 åxi
a1 =		i =1		i =1		.	(7.11)
				N

По найденным значениям свободных параметров а1 и а2 строится аппроксимирующая прямая.

7.4. Статистические гипотезы и их проверка

Экспериментальное определение физических величин, как правило, сопровождается помехами, из-за чего результаты измерений представляют собой случайные величины. Кроме расчета статистических характеристик случайных величин (математического ожидания, дисперсии, среднеквадратичного отклонения и т.д.) основной задачей статистического анализа результатов исследования (наряду с дисперсионным и регрессионным анализами) является проверка статистических гипотез.

Под статистическими гипотезами понимаются некоторые предположения относительно свойств генеральной совокупности той или иной случайной величины. Например, предполагают, что генеральная совокупность распределена по нормальному закону – гипотеза нормальности, гипотеза о равенстве математического ожидания заданному значению и др. Проверка гипотезы заключается в сопоставлении некоторых статистических показателей, критериев проверки, вычисляемых по выборке, со значениями этих показателей, определенных теоретически в предположении, что проверяемая гипотеза верна.

Чтобы принять или отвергнуть гипотезу, еще до получения выборки задаются уровнем значимости a. Наиболее употребителен в технике уровень значимости 0,05 (хотя могут быть использованы и другие – 0,1; 0,02; 0,01; 0,001 и т.д.) Меньшие a соответствуют данным, полученным с высокой точностью и в большом объеме. Уровню значимости соответствует доверительная вероятность Р=1 – a. По этой вероятности, используя гипотезу о распределении оценки q* (критерия значимости), находят доверительные (квантильные) границы, как правило, симметричные qa/2 и q1-a/2 . Числа qa/2 и q1-a/2 называют критическими значениями гипотезы; значения θ*, меньшие чем qa/2 и большие чем q1-a/2 , образуют критическую область гипотезы или область непринятия гипотезы. Если найденное по выборке значе-

72

ние q0 попадает между qa/2 и q1-a/2 , то гипотеза допускает такое значение в качестве случайного, и поэтому нет оснований ее отвергать. Если же найденное значение θ0 попадает в критическую область, то гипотеза отвергается. При этом можно совершить ошибку и отвергнуть гипотезу, которая на самом деле верна. Однако вероятность такой ошибки не больше принятого уровня значимости. Например, при a = 0,05 можно совершить ошибку в пяти случаях из ста.

Рассмотрим кратко лишь те законы распределения или критерии, которые наиболее часто применяются в теории эксперимента.

Критерий распределения Стьюдента применяется, когда необходимо сделать статистический вывод, равно ли математическое ожидание М{х} генеральной совокупности некоторому предполагаемому значению с, или когда

нужно построить доверительный интервал для величины М{x}:
t =			- m
		x					(7.12)
					n
			s

Здесь x – нормально распределенная случайная величина; n - объем выборки; под µ здесь подразумевается либо с, либо М{х}; s – корень квадратный из выборочной дисперсии.

Если при расчете t по (7.12) окажется, что t < tкр, то делается вывод, что гипотеза М{х} = с не противоречит результатам наблюдений при принятом уровне значимости а, в противном случае эта гипотеза отвергается.

Критерий Пирсона (c2 - критерий) применяется в основном для того,

чтобы по известной выборочной дисперсии s2 судить о генеральной дисперсии σ2:

N æ x

-

ö2

x2 =

i

x

ç

÷

(7.13)

åç

s{x}

÷

è

ø

i =1

С его помощью рассчитываются доверительные границы для генераль-

ной дисперсии:

(n -1)s 2 {x}

< s2

{x}<

(n -1)s 2 {x}

,

(7.14)

x2

x2

2

1

где x 2

и x 2

находят из таблиц по

f = n -1 степеням свободы и по уровням

1

2

значимости a1 =1 - a/2; a2 =a/2 (здесь a – принятый уровень значимости). Критерий Фишера (F-критерий) применяется для решения задач от од-

нородности генеральных дисперсий путем сравнения выборочных дисперсий

s 2	и s 2	(проверка однородности дисперсий:
1	2
		F = s 2	/ s 2	,	(7.15)
		1	2

73

причем в числитель ставится большая из двух дисперсий. Если F<Fкр, то принимается гипотеза о равенстве генеральных дисперсий s12 {x}= s22 {x} при

принятом уровне значимости a.

Критерий Кохрэна (G-критерий) применяется для проверки однородности многих дисперсий, но определенных с одними и теми же степенями свободы (т.е. определенных по одним и тем же выборкам):

G = s12	n
	/ åsi2 ,	(7.16)
	i =1

где s 2	– наибольшая выборочная дисперсия.
1
Для выявления промахов или грубых ошибок служит t-критерий:
	t =		x -		/ s;	(7.17)
				x

здесь х – крайний (подозрительный) элемент выборки.

Применяется этот критерий так: по таблицам определяют значение t1-a, и если t < t1-a, то выпадение х случайно и выбрасывать его нельзя, если t > t1-a, то это промах и его следует отбросить.

7.5. Дисперсионный и регрессионный анализы

Цель дисперсионного анализа определить, влияют ли факторы х на у на фоне помех. Различают однофакторный (у зависит от одного фактора) и многофакторный (у зависит от нескольких факторов) дисперсионный анализ. Чтобы решить, значимо ли влияние данного фактора, необходимо оценить значимость соответствующей выборочной дисперсии в сравнении с дисперсией воспроизводимости, обусловленной случайными факторами.

Рассмотрим однофакторный дисперсионный анализ. В самом простом случае дисперсия наблюдений σ2 известна заранее и исследуется один переменный фактор х. Пусть в этом случае при изменении фактора х получились результаты наблюдений у1, у2,..., уn. Найдем выборочную дисперсию s2.

Сравним эту дисперсию с генеральной дисперсией σ2. Если s2 от σ2 отличается незначимо, то и влияние фактора х нужно признать незначимым. Если же s2 отличается значимо от σ2, то это может быть вызвано только влиянием фактора х, которое следует признать значимым. Факт значимости устанавли-

вается по критерию Фишера F = s 2 / s2 . Задавшись уровнем значимости a, найдем табличное значение F1-a . Если F < F1-a , то дисперсии s2 и σ2 однородны и x не влияет на у. Если F > F1-a , то s2 и σ2 неоднородны и х влияет на у на фоне помех.

Однако часто бывает так, что заранее дисперсия σ2 неизвестна. Рассмотрим снова действие единичного фактора х, который принимает n различных значений (уровней фактора). На каждом i-м уровне производится m

74

наблюдений (примем m одинаковыми для каждого уровня, в этом случае расчеты наиболее просты). Обозначим через yi среднее значение наблюдений на i-м уровне:

				m
				å yij
			=	i =1	.	(7.18)
	y	i
				m

Вычислим выборочную дисперсию на каждом уровне:

	si2 =	1		å(yij -			)2 .	(7.19)
					y	i
		m -1

Для проведения дисперсионного анализа необходимо общую выборочную дисперсию

		ån åm (yij -		i )2
			y
	s 2 =	i =1i =1			(7.20)
		mn -1

разложить на составляющие, которые характеризовали бы вклад фактора х и фактора случайности.

Если дисперсии (7.19) однородны (это можно проверить по критерию Кохрэна), то хорошей оценкой дисперсии, характеризующей фактор случайности, является

		n
		åsi2
s 2	=	i =1	.	(7.21)
0		n

Общее среднее для всей выборки из nm наблюдений равно

			n
		å			i
				y
		=	i=1			.	(7.22)
	y
			n

Дисперсия, характеризующая вклад фактора х, рассчитывается по соотношению

sx2 =	m	ån (		i -		)2 .		(7.23)
					y
			y
	n -1 i =1
Далее, используя критерий Фишера F = s 2							/ s 2	и сравнивая его с таб-
						x	0

личным значением при выбранном уровне значимости, можно сделать вывод о значимом или незначимом влиянии х на у.

Если дисперсионный анализ отвечает на вопрос, влияет ли данный фактор (факторы) на у, то задачей регрессионного анализа является выяснение количественных характеристик этого влияния.

При использовании статистических методов уравнение связи параметров процесса (математическая модель) чаще всего представляется в виде

уравнения регрессии

75

N	N	N
y = b0 + åbi xi +	å bui xu xi + åbii xi2 + ....		(7.24)
i =1	u,i =1	i =1
	u ¹i

Коэффициент b0 называют свободным членом уравнения регрессии; коэффициенты bi – линейными эффектами; коэффициенты bii – квадратич-

ными эффектами; bui– эффектами парного взаимодействия. Коэффициенты уравнения (7.24) определяются методом наименьших квадратов с учетом среднеквадратичных погрешностей зависимой и независимой переменных. Случай, когда независимые переменные определены точно, рассмотрен ранее (аппроксимация).

После того как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Он заключается в проверке значимости всех коэффициентов регрессии и адекватности уравнения. Предварительно необходимо проверить однородность дисперсий.

Оценка значимости коэффициентов производится по критерию Стью-

дента
ti =		bi		/ sb ,	(7.25)
				i

где bi – i - й коэффициент уравнения регрессии; sbi . –среднеквадратичное отклонение i-го коэффициента.

Для

линейной

регрессии

от

одного

параметра

sвоспр2

n

2j

å x

sвоспр2

n

sb

=

j =1

; sb

=

(7.26)

n

æ

n

ö

2

n

æ

n

ö2

0

1

n å x 2j

-

ç

å x j

÷

n å x 2j

- ç

å x j

÷

j =1

ç

÷

j =1

ç

÷

è j =1

ø

è j =1

ø

1

n

m

(y ji - y j )2

Здесь sвоспр =

å å

дисперсия воспроизводимости.

n(m -1)

j =1u =1

Если ti больше табличного ta для выбранного уровня значимости a, то

коэффициент bi значимо отличается от нуля.

Незначимые коэффициенты исключаются из уравнения регрессии. Оставшиеся коэффициенты пересчитываются заново, поскольку они статистически связаны друг с другом.

Проверить адекватность уравнения – это значит убедиться в том, что оно достаточно верно описывает качественно и количественно реальный процесс. Адекватность уравнения проверяется по критерию Фишера

F = sад2 / sвоспр2 . (7.27)

Здесь sад2 – дисперсия адекватности.

76

Для одинакового числа дублирующих опытов sад2 вычисляется по соотношению

		n			2
				)
		m å (y j - y j )
sад2	=	j =1				,	(7.28)
		n -1

где yˆ – значение у, рассчитанное по уравнению регрессии.

Если F меньше табличного значения F1-a для уровня значимости a, то уравнение адекватно эксперименту.

Контрольные вопросы

1.Назовите и охарактеризуйте способы проверки результатов измерений.

2.Поясните аппроксимацию результатов эксперимента.

3.В чем заключается интерполяция и экстраполяция полученных результатов?

4.Охарактеризуйте основные положения графического анализа.

5.Как проверяются статистические гипотезы?

6.Поясните основные положения дисперсионного и регрессионного анализа?

8.МЕТОДЫ ПЛАНИРОВАНИЯ АКТИВНОГО ЭКСПЕРИМЕНТА

8.1.Основные понятия и виды планов.

Математическое планирование экспериментов, которое предшествует постановке физического, математического и аналогового экспериментов и сопровождает их выполнение, является средством сокращения числа экспериментов и повышения достоверности выявляемых при исследовании зависимостей. Целью математического планирования эксперимента может быть также отыскание экстремальных значений исследуемых зависимостей с наименьшей затратой средств и времени или уточнение коэффициентов в выражающих их уравнениях.

Эмпирическую зависимость, которая выявляется в эксперименте, будем называть уравнением регрессии. Она выражается функцией отклика, связывающей результат эксперимента (или параметр оптимизации) с переменными параметрами, которыми варьируют при проведении опытов:

y = j(x1, x2 ,..., x N ).

(8.1)

Независимые переменные х1, x2, ..., xN принято называть факторами, а их значения (для каждого фактора n значений) – уровнями факторов. Координатное пространство с координатами х1, x2, ..., xN называют факторным

77

пространством, а геометрическое изображение функции отклика в фактор-

ном пространстве – поверхностью отклика.

Различают основные и случайные факторы. К основным факторам относятся все изучаемые факторы, а также другие учитываемые и измеряемые факторы, служащие для стабилизации процесса. Все прочие неустраняемые факторы, не поддающиеся учету и измерению, относят к случайным факторам.

Если в эксперименте выявляется зависимость у от одного фактора х, то такой эксперимент называют однофакторным. Когда на у влияет несколько факторов, то имеет место многофакторный эксперимент.

При использовании методики однофакторного эксперимента в многофакторном эксперименте предполагается, что исследователь может с любой степенью точности стабилизировать все независимые переменные системы, затем, поочередно изменяя некоторые из них, возможно определение искомых зависимостей. Такой эксперимент называют еще пассивнымНеобоснованно. завышенное число уровней факторов n, имеющее место при использовании методики однофакторного эксперимента, приводит при многофакторном исследовании к резкому увеличению необходимого числа опытов (nN). Так, например, для полного исследования влияния четырех факторов, каждый из которых может принимать по 5 значений (5 уровней), потребуется проделать 54=625 различных комбинаций экспериментов. Исследователи, пользующиеся классической методикой однофакторного эксперимента, как правило, вынуждены ограничивать число экспериментов путем исследования только части существенных факторов (уменьшение N), уменьшения числа уровней каждого из факторов (уменьшение n) или исследования влияния каждого из факторов только при некоторых частных значениях других факторов. При этом страдает прежде всего достоверность уравнения регрессии.

Под планированием эксперимента (ПЭ) понимается постановка опытов по заранее составленной схеме, обладающей какими-то оптимальными свойствами.

Можно выделить два основных направления в теории ПЭ: планирование экспериментов по выяснению механизма явлений и планирование экстремальных экспериментов. Планирование первого типа применяется для нахождения уравнения регрессии. Во втором случае экспериментатора интересуют условия, при которых изучаемый процесс удовлетворяет некоторому критерию оптимальности.

Планирование эксперимента представляет собой новый подход к исследованиям, который позволяет успешно решать наиболее важные для исследователя вопросы: сколько и каких опытов следует провести, как обработать их результаты, чтобы решить поставленную задачу с заранее заданной точностью при минимально возможном числе опытов.

Методы ПЭ применимы к любым простым и сложным системам, обладающим свойством управляемости (значения факторов можно менять по же-

78

ланию экспериментатора) и необходимой степенью воспроизводимости результата.

Втеплофизическом эксперименте (для исследования характеристик объектов теплоэнергетики), имеющем свою специфику, математическое планирование не нашло широкого применения, хотя необходимость в этом имеются, так как в этом случае существует воспроизводимость результатов и возможность измерять и целенаправленно изменять переменные. Теплофизический эксперимент часто обладает высоким уровнем априорной информации, т.е. процессы (например, процессы тепломассообмена и трения) с той или иной степенью приближения описываются системой дифференциальных уравнений. В таком эксперименте есть возможность предварительно выявить методами обобщенных переменных или локального моделирования зависимые и независимые обобщенные переменные. Использование этой возможности позволяет сократить число переменных, влияние которых предполагается изучать. При использовании методов ПЭ в таком эксперименте в качестве факторов следует использовать эти обобщенные переменные. В той области теплофизического эксперимента, где не удается выявить обобщенные переменные, в качестве факторов при ПЭ используют абсолютные величины влияющих параметров.

Следует отметить, что ПЭ предъявляет повышенные требования к тщательности проведения эксперимента. Статистические оценки результатов реализации плана эксперимента неизбежно отразят недостатки в экспериментировании.

ВПЭ используются понятия планов первого и второго порядков, ортогональных и ротатабельных планов. Под планами первого порядка понимают такие планы, которые позволяют провести активный эксперимент для отыскания уравнения регрессии, содержащего только первые степени факторов и их произведения. Планы второго порядка позволяют провести активный эксперимент для отыскания уравнения регрессии, содержащего вторые степени факторов. В дальнейшем увеличении порядка планов чаще всего нет необходимости.

Уравнение регрессии должно быть адекватным, т.е. оно должно в некоторой области соответствовать реальному процессу с требуемой точностью.

Ортогональные планы – это специальным образом составленные планы, обладающие диагональной матрицей системы нормальных уравнений (в такой матрице все члены, кроме расположенных по диагонали, равны нулю)

ив связи с этим обеспечивающие простоту вычислений, независимость определения всех коэффициентов уравнения регрессии. Каждый коэффициент в таких планах определяется по результатам всех опытов.

Ротатабельные планы – это таким образом составленные планы, что все коэффициенты уравнения регрессии определяются с одинаковой дисперсией.

При построении плана эксперимента каждый исследователь стремится сделать этот план в определенном смысле оптимальным. К параметрам пла-

79

на, которые обычно оптимизируются, относят число опытов в плане, степень использования факторного пространства, среднюю или максимальную дисперсию найденных коэффициентов, среднюю или максимальную дисперсию результата эксперимента и т.д. Естественно, что каждому оптимизируемому параметру соответствует свой критерий оптимальности, на основании которого производят выбор наилучшего варианта плана. Используют, например А

– G-оптимальные планы, обеспечивающие наименьшие значения соответственно средней дисперсии найденных коэффициентов уравнения и максимальной дисперсии результата эксперимента.

8.2. Рациональное планирование

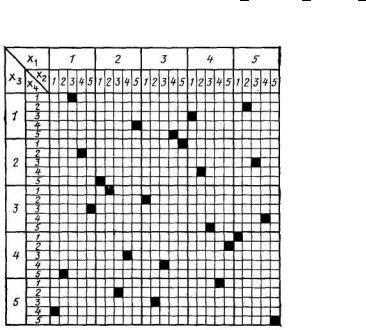
Рациональное планирование экспериментов позволяет при минимальном числе опытов наиболее равномерно охватить всю площадь таблицы возможных сочетаний влияющих факторов. В этом случае эксперимент планируется так, чтобы ни в одной строке и ни в одном столбце не было повторных сочетаний. На рис. 8.1 показан один из возможных планов такого сочетания четырех факторов, каждый из которых может принимать пять значений.

Номер столбца средних (по значению) квадратов соответствует номеру уровня фактора х1, а номер строки средних квадратов – номеру уровня фактора х3. Из 25 возможных сочетаний факторов х2 и х4 в каждом из средних квадратов мы выбираем только одно, обозначенное зачерненной клеткой, причем в каждой строке и в каждом столбце мелких квадратов должна быть только одна такая клетка. Нетрудно убедиться, что для каждого уровня одного из факторов, например для x1= 1, все уровни прочих факторов встречаются одинаково часто. Так, в этом случае: х2 = 3, 4, 5, 2, 1; х3 = 1, 2, 3, 4, 5 и х4 = 1, 2, 3, 5, 4.

Поэтому при определении результатов для х1= 1 влияние трех других факторов усреднится и результат будет соответствовать х 2 = 3; х3 = 3; х4 = 3.

Рис. 8.1. Рациональный план эксперимента для четырех факторов

80