НИРС Андреев / МНИ

Dx = tan Snn .

Доверительная вероятность a выбирается близкой к единице на осно-

вании практических соображений. Значения коэффициента tαn приводятся в таблицах. Доверительный интервал, в котором содержится истинное значение искомой величины xист, с заданной вероятностью определится границами

x - x £ xист £ x + x.

9.Окончательный результат записывается в виде

x= x ± Dx , Р.

6.6. Оценка погрешности определения величин-функций (косвенных измерений)

Необходимость в определении погрешности величин-функций по известным значениям погрешностей их аргументов возникает при оценке точности результатов математического и аналогового экспериментов, а также результатов косвенных измерений. Во всех этих случаях искомая величина находится из соотношения

Y = j( X1, X 2 ,..., X n ),

(6.24)

где Х1, Х2, ..., Хn – аргументы, определенные независимо друг от друга.

В дальнейшем будем полагать, что погрешность определения величины Y обусловлена лишь неточностью численных значений величин Х1, Х2, …, Хn, входящих под знак функции, а дополнительная погрешность, связанная с округлениями при вычислениях или возможным использованием приближенных методов решения уравнения (6.24), во внимание не принимается.

Погрешность определения каждого аргумента Xi приводит к появлению составляющей погрешности DYi величины Y

DY =	¶j	DX	i	.	(6.25)
i	¶X i

Доверительная вероятность, соответствующая величине DYi - численно

равна доверительной вероятности, с которой найдена погрешность DXi.

Для относительных погрешностей вместо соотношения (6.25) используется выражение

di =	1		¶j	DX i =	¶ ln j DX i .	(6.26)
	j ¶X i				¶X i

Общая абсолютная (DYS) или относительная (dS) погрешности определения функции могут быть найдены с помощью выражений

	n		m
DYå = ± å(DYi/ )2		+ k 2	å(DYi// )2 ;		(6.27)
	i =1		i =1

61

	n		m
då = ± å(di )2		+ k 2	å(di// )2 .		(6.28)
	i =1		i =1

Здесь n и m – число составляющих погрешности, имеющих соответственно нормальный и равномерный закон распределения; параметры, снабженные одним штрихом, представляют собой погрешности, имеющие нормальный закон распределения, а снабженные двумя штрихами – равномерный закон распределения.

Доверительная вероятность абсолютной DYS и относительной dS погрешностей, определенных из соотношений (6.27) и (6.28), численно равна доверительной вероятности, при которой выбираются составляющие погрешности, имеющие нормальный закон распределения, а также параметр k. Составляющие погрешности, имеющие равномерный закон распределения, при подстановке в формулы (6.27) и (6.28) выбираются при доверительной вероятности, равной единице.

Соотношения (6.27), (6.28) получены при допущении, что результирующая погрешность от составляющих с равномерным распределением имеет нормальное распределение.

Для доверительной вероятности Р = 0,95 параметр k » 1, а выражения (6.27), (6.28) можно представить в более простой форме:

	n +m				n +m
DYS = ± å		DYi2 ;		dS = ± å di2 .			(6.29)
	i =1				i =1

Частные производные, входящие в соотношения (6.25) и (6.26), не всегда могут быть взяты аналитически. Часто не удается разрешить исходную задачу в явном виде относительно искомой величины Y или же функция j

(Х1, Х2,..., Хn) имеет чрезвычайно сложный вид. В этих случаях предпочтительным или даже единственно возможным оказывается численный метод определения производных.

Контрольные вопросы

1.Напишите формулу для определения абсолютной и относительной погрешности.

2.Назовите причины возникновения погрешностей.

3.Какие погрешности называются систематическими, случайными и грубыми?

4.Дайте классификацию систематических погрешностей.

5.Какие вы знаете показатели точности и формы представления результатов эксперимента?

6.Как оцениваются погрешности прямых измерений?

7.Опишите правила записи и вычислений результатов измерений.

8.Дайте алгоритм обработка результатов прямых многократных измере-

62

ний.

9.Напишите общую формулу для определения погрешности косвенных измерений.

7. МАТЕМАТИЧЕСКИЕ ПРИЕМЫ АНАЛИЗА И ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

7.1 Способы проверки полученных результатов

При проведении физического, аналогового или математического эксперимента даже использование самых современных средств измерений, тщательно проверенных методик проведения эксперимента и обработки его результатов, отлаженных и апробированных вычислительных программ для ЭВМ и т.д. не гарантирует от получения недостоверных результатов. Причинами, приводящими к получению недостоверных данных, могут быть: выход из строя средств измерений во время эксперимента, промахи, допущенные при снятии показаний приборов, ошибки, допущенные при подготовке исходных данных для аналогового или математического эксперимента, сбой в работе ЭВМ, потеря устойчивости вычислительного алгоритма и пр.

Для того чтобы исключить влияние указанных случайностей на результаты экспериментов, исследователь должен предусмотреть систему проверок результатов эксперимента. Часть этих проверок может быть основана на использовании аналитических приемов, которые в некоторых случаях позволяют обнаружить источник ошибки. Остановимся на основных из них.

Применение законов сохранения. Возможна проверка только тех опытных данных, для которых можно записать одно или несколько уравнений сохранения (уравнения сохранения массы, количества движения, энергии, электрического заряда и т.д.). Критерием достоверности результатов эксперимента является удовлетворение их с требуемой точностью уравнению сохранения.

Реализация такой проверки может потребовать некоторого усложнения экспериментальной установки и методики проведения эксперимента или вычислительного алгоритма с целью определения дополнительных величин, необходимых для составления материального баланса.

Использование известных закономерностей поведения исследуемой величины. Во многих случаях оказывается возможным еще до проведения эксперимента теоретически или из анализа физической природы явления определить значение исследуемой величины в некоторых характерных точках системы, например ее предельное значение, а также оценить степень влияния на нее различных факторов. Так, сила тока равна нулю при нулевом напряжении, тепловой поток между телами равен нулю при отсутствии между ними перепада температуры и неограниченно возрастает при его неограниченном увеличении, расход жидкости в трубопроводе равен нулю при отсутствии перепада давления и т.д.

63

Проверка результатов эксперимента рассматриваемым методом заключается в сопоставлении данных, полученных в процессе исследования, с имеющимися сведениями о характере их изменения.

Анализ резко отклоняющихся значений. Практически почти в каж-

дом эксперименте среди опытных данных содержится некоторое число точек, существенно отклоняющихся от общей закономерности. Часть этих точек или даже все они могут быть ошибочными, и их следует отбросить, чтобы они не могли, исказить результатов эксперимента и повлиять на окончательные выводы. Следует, однако, иметь в виду, что при отбрасывании таких выпадающих из общей закономерности точек существует риск исключить верные данные и потерять важные результаты, поскольку отклонение опытных точек может быть обусловлено физической природой явления, поэтому при их выбраковке следует руководствоваться следующими правилами:

а) резко отклоняющиеся точки необходимо исключить из дальнейшего рассмотрения, если их ошибочность подтверждена с помощью какого-либо другого метода, описанного выше;

б) если подтвердить ошибочность опытных точек с помощью других методов не удалось, то точки, лежащие вблизи границ диапазона изменения в экспериментах влияющего параметра, необходимо сохранить, так как они могут характеризовать особенности изучаемого явления; точки, лежащие в середине этого диапазона, следует сохранить только в том случае, если статистический анализ данных подтверждает принадлежность этих точек и всей остальной массы к одной и той же совокупности.

Существует ряд статистических критериев для исключения опытных точек.

7.2. Математическая обработка результатов эксперимента

После получения достаточного количества экспериментальных данных и отсева ошибочных результатов проводят их дальнейший анализ и обработку, позволяющие выявить новую информацию об изучаемом явлении. Для этого приходится аппроксимировать опытные данные аналитической функцией, выполнять операции интерполяции и экстраполяции, дифференцировать и интегрировать полученные результаты и т.д.

Аппроксимация результатов эксперимента. Аппроксимации экспе-

риментальных результатов должно предшествовать изучение характера их поведения на определенном участке изменения аргумента и его сопоставление с характером изменения хорошо изученных функций. Вид аппроксимирующей функции Р(х) выбирается на основе этого сопоставления, а если возможно, то и исходя из условия соответствия физической природе явления или имеющимся представлениям об особенностях поведения исследуемой величины.

64

Близость значений функции Р(х) и экспериментальных результатов φ(xi) в точках x = xi обеспечивается введением в аппроксимирующую функ-

цию n свободных параметров an и соответствующим их выбором. Существуют два различных способа нахождения свободных парамет-

ров. Выбор того или иного из них определяется целями и задачами, стоящими перед исследователем, точностью полученных результатов, их количеством и т.д.

Первый способ базируется на удовлетворении условию, чтобы функция Р(х, а) совпадала с экспериментальными значениями в n точках, выбранных в качестве опорных (число свободных параметров не должно превышать числа имеющихся опытных точек). В этом случае для определения n неизвестных

значений параметров an используется система n уравнений

	P(x1, a1, a2 ,..., an ) = j(x1 );
	P(x2 , a1, a2 ,..., an ) = j(x2 );	(7.1)
	..........................................
	P(xn , a1, a2 ,..., an ) = j(xn ).

После определения численных значений параметров аn проверяется качество аппроксимации путем сопоставления значений функции и экспери-

ментальных данных в оставшихся точках хi рассматриваемого интервала. Если обнаруженные между ними расхождения превышают допустимые по условиям точности, то аппроксимацию следует повторить, приняв в качестве опорных другие точки или увеличив число свободных параметров.

В предельном случае, когда число свободных параметров равно числу экспериментальных точек в рассматриваемом интервале изменения аргумента, все экспериментальные точки будут совпадать со значениями функции. Следует заметить, что добиваться точного совпадения значений функции и экспериментальных данных путем значительного увеличения числа свободных параметров часто неразумно, поскольку экспериментальные результаты получены с большей или меньшей погрешностью, и такая функция может не отражать действительного характера изменения исследуемой величины (кривая 1 на рис. 7.1). На этом рисунке σ – среднеквадратичная погрешность результатов эксперимента.

Второй способ определения свободных параметров основан на выполнении требования, чтобы сумма квадратов отклонений экспериментальных точек от соответствующих значений аппроксимирующей функции была минимальной. Этот способ носит название метода наименьших квадратов. Заметим, что можно оперировать и суммой других четных степеней этих отклонений (невязок), но тогда вычисления будут сложнее, однако руководствоваться суммой самих невязок нельзя, так как она может оказаться малой и при больших отклонениях противоположного знака.

65

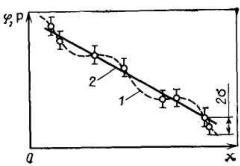
Рис. 7.1. Аппроксимация опытных данных представленных точками:

1 – аппроксимирующая функция с большим числом свободных параметров; 2 – аппроксимирующая функция с небольшим числом свободных параметров, определенная методом наименьших квадратов

Математическая запись приведенного выше требования имеет вид

s = åN [P(xi , a1, a2 ,..., an )- j(xi )]2 = min,	(7.2)
i =1

где N – число экспериментальных точек в рассматриваемом интервале изменения аргумента х.

Неизвестные значения свободных параметров аn определяются в результате решения задачи на поиск минимума функции s. Необходимыми условиями экстремума функции являются

¶s

= 2

N ì[P(x

, a , a

,..., a

)- j(x

)]

¶P

ü = 0;

ü

¶a

i

2

n

i

¶a

ï

åí

1

ý

1

i =1î

1

þ

ï

¶s

N

¶P

ï

= 2

ì[P(x

, a , a

,..., a

)- j(x

)]

ü = 0;ï

å

i

2

n

i

¶a2

í

1

ý

ï

(7.3)

i =1î

¶a2 þ

ý

.............................................................................

ï

ï

¶s

N

ì[P(x

,...,)- j(x

)]

¶P ü

ï

= 2

å

, a , a

= 0.

ï

i

2

ii

ý

¶an

í

1

ï

î

¶an þ

i =1

þ

Из физического смысла решаемой задачи следует, что условиям (7.3) соответствует минимум функции s.

Таким образом, для определения n неизвестных параметров аn имеется система n уравнений. Часто в качестве аппроксимирующей выбирается функция вида

P = a	+ a	2	x + a	3	x2	+ ... + a	n	xn -1.	(7.4)
1

Применительно к выражению (7.4) система уравнений (7.3) примет вид

66

¶s

N

ü

=

2 å [a1

+ a 2 x i + a 3 x i2 + ... + a n x in -1 - j (x i )]= 0 ;

ï

¶a1

i =1

ï

¶s

N

2

n -1

ï

2 å {[a1 + a 2 x i

- j (x i

)]x i }=

ï

=

+ a 3 x i

+ ...

+ a n x i

0;

ï

(7.5)

¶a 2

i =1

ý

.......... .......... .......... .......... .......... .......... .......... .......... ........

ï

ï

¶s

N

ï

=

2 å {[a1 + a 2 x i

+ a 3 x i2

+ ...

+ a n x in -1 - j (x i )]x in -1

}=

0 .ï

¶a

n

i =1

ï

þ

После несложных преобразований системы уравнений (7.5) получается

N

N

N

N

N

);

ü

a1N + a2

åxi + a3 åxi2 + ... + an åxin-1 = åxin

-1

= åj(x

ï

i =1

i -1

i =1

i =1

i

ï

i =1

N

N

N

2

N

3

N

n

N

ï

a1 åxi

= åxij(xi );

ï

+ a2 åxi + a3 åxi

+ a3 åxi + ... + an åxi

ï

(7.6)

i =1

i =1

i =1

i =1

i =1

i =1

ý

...........................................................................................................

ï

ï

N

xn-1 + a

N

xn + a

N

xn+1 + ... + a

N

N

ï

a

x2n-2

=

xn-1 * j(x

).ï

1

å i

2 å i

3

å i

n å i

å i

i

ï

i =1

i =1

i =1

i =1

i =1

þ

Система (7.6) представляет собой систему n уравнений первой степени с n неизвестными значениями параметров аn .Величины N, хi, φ(хi) известны из эксперимента. При n≤N система имеет единственное решение, которое может быть получено с использованием ЭВМ. При n = N численные значения свободных параметров, определенных по первому и второму способам, идентичны, а все опытные точки совпадают с аппроксимирующей зависимостью. При n > N системы уравнений (7.1), (7.3) и (7.6) переопределены и допускают множество решений. Так же как и в предыдущем случае, стремиться к значительному увеличению числа свободных параметров обычно нецелесообразно не только из-за существенного усложнения аппроксимирующей функции и ее дальнейшего использования, но и из-за того, что хорошее сглаживание погрешностей эксперимента будет иметь место лишь в случае n << N. В то же время для удовлетворительного описания достаточно сложного характера изменения определенной опытным путем величины требуется увеличить число n.

Оптимальное число свободных параметров определяют из условия dn = s , где dn – среднеквадратичное отклонение опытных точек от аппрок-

	симирующей зависимости dn =		s		;	s – среднеквадратичная погреш-
			N -1

ность эксперимента.

Условие dn >> σ означает, что математическая погрешность аппроксимации много больше погрешности опытных данных, поэтому следует увели-

чить число свободных параметров. При dn << σ часть свободных параметров

67

недостоверна и надо уменьшить n. Если при выбранном исходя из указанных соображений значении n выполняется условие n << N, то вид аппроксимирующей функции выбран удачно. При n » N следует подобрать более подходящий вид аппроксимирующей функции.

Пример аппроксимации опытных данных функцией вида (7.4) методом наименьших квадратов с числом параметров n = 2, близким к оптимальному, показан на рис. 7.1 (линия 2).

В тех случаях, когда отыскивается функция, зависящая от нескольких факторов, задача несколько усложняется, хотя рассмотренные выше применительно к функции одного переменного принципы сохраняются и здесь. При достаточно большом числе влияющих факторов оправдано использование теории планирования эксперимента, открывающей возможность отыскания аппроксимирующей функции наиболее рациональным путем с одновременным контролем качества аппроксимации.

Интерполяция и экстраполяция. Если проведению операций интерполяции предшествовало нахождение аппроксимирующей функции, то значение искомой величины в нужных точках проще всего найти с использованием полученного уравнения, в противном случае можно воспользоваться графическим способом или, что особенно удобно при обработке данных на ЭВМ, готовыми интерполяционными формулами. Так, если в результате экс-

перимента получена совокупность значений (х1, j1); (х2, j2); ...; (хn, jn), то величина j при значении аргумента х, не реализованном в опыте, определяется с использованием интерполяционной формулы Лагранжа

j = j1

(x - x2 )(x - x3 )...(x - xn )

+

(x

- x

2

)(x

- x

3

)...(x

- x

n

)

1

1

1

+ j2

(x - x1 )(x - x3 )...(x - xn )

+ ...

(7.7)

(x

2

- x )(x

2

- x

3

)...(x

2

- x

n

)

1

... + jn

(x - x1 )(x - x2 )...(x - xn -1 )

.

(x

n

- x )(x

n

- x

2

)...(x

n

- x

n -1

)

1

В последнее время все чаще применяется интерполяция опытных данных с использованием так называемых сплайнов. При этом предварительно весь диапазон исследования разбивают на некоторое (в общем случае произвольное) число участков, а в пределах каждого участка результаты эксперимента аппроксимируют многочленом вида (7.4). Часть свободных параметров каждого такого многочлена, имеющего степень n – 1, определяется из условия обеспечения непрерывности функции и ее производных до (n – 2)-го порядка включительно на границах соседних участков. Остальные параметры определяются методом наименьших квадратов. Функцию вида (7.4), аппроксимирующую экспериментальные результаты на каждом выделенном участке изменения аргумента и непрерывную вместе со своими производными до (n – 2) - го порядка включительно на внутренних границах участков, и называют

68

сплайном.

Экстраполяцию результатов исследования во избежание серьезных ошибок следует применять с большой осторожностью, но в то же время полностью игнорировать ее возможностей нельзя, так как в некоторых случаях это единственный путь получения или проверки новых результатов.

Дифференцирование и интегрирование. При численном дифферен-

цировании таблицы экспериментальных данных возможность получения приемлемых результатов часто ограничена, так как последние очень чувствительны к погрешностям эксперимента. Удовлетворительные результаты в этом случае могут быть получены лишь после выполнения каким-либо способом операции сглаживания результатов эксперимента, например, графическим путем или с помощью их аппроксимации методом наименьших квадратов функцией с относительно небольшим числом свободных параметров (n << N). Последний способ удобен еще и потому, что позволяет проводить дифференцирование полученной функции аналитически.

Интегральные характеристики гораздо менее чувствительны к погрешностям эксперимента, поскольку погрешности противоположного знака компенсируют друг друга; поэтому возможно численное интегрирование таблицы экспериментальных результатов без их предварительного сглаживания. Однако если ранее была получена аппроксимирующая функция, то операцию интегрирования удобно проводить над ней аналитическим способом.

7.3. Графический анализ

Редкое экспериментальное исследование обходится без построения графиков и их анализа. Обладая большой простотой и наглядностью при небольших затратах труда, графический способ анализа позволяет получить решение многих из стоящих перед исследователем задач. По сравнению с математическими приемами анализа графический способ обладает невысокой точностью, поэтому его наиболее целесообразно использовать в процессе предварительной обработки данных для выявления качественных закономерностей исследуемого явления, для иллюстрации результатов математического анализа и представления полученных результатов.

Для того, чтобы с помощью графика можно было получить максимум информации об исследуемом явлении, его размеры, масштабы для координатных осей и разметка шкал должны быть выбраны такими, чтобы цена наименьшего деления соответствовала примерно значению среднеквадратичной погрешности исследуемой величины. Если будет выбран значительно более крупный или мелкий масштаб, то соответственно в первом случае большой разброс опытных точек может затруднить или даже сделать невозможным установление закономерности изменения исследуемой величины, а во втором случае случайные отклонения полностью сгладятся и из графика невозможно сделать заключение о качестве эксперимента. Сказанное иллюстрирует рис. 7.2. Масштаб графика 7.2, в выбран правильно.

69

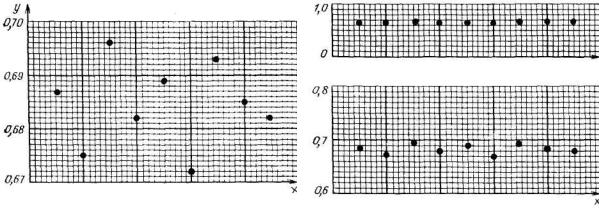
б

а

в

Рис. 7.2. К выбору масштаба для координатных осей

Очень часто бывает удобным или даже необходимым систему координат выбрать так, чтобы экспериментальные точки в этой системе группировались около прямой линии. Имея результаты, которые в той или иной системе координат могут быть представлены в виде прямой, легко найти одним из описанных выше методов ее уравнение и после преобразования координат получить эмпирическую формулу. В табл. 7.1 приведена сводка формул для преобразования системы координат с целью получения линейной зависимости применительно к некоторым часто используемым функциям.

Таблица 7.1

Вид функции

Новые переменные

Ось абсцисс ξ

Ось ординат η

y = ax + b

x

y

y = axb

log x*

log y*

y = a ×10bx

x

log y*

y = aebx

x

log y*

y =

x

1

, x

1

,

x

a + bx

x

y

y

x

x

x - x1**

y = a + bx + c

y - y1

y = a + bx + cx2

x

y - y1**

x - x1

y = a ×10bx+cx

2

x

**

log y - log y1

x - x1

y = aebx+cx2

x

log y -log y1**

x - x1

70