По этому уравнению в лабораторных условиях обычно определяют проницаемость пластовой породы. Для этого её образец (цилиндрической формы) длиной l и площадью сечения w помещают в патрон с резиновым уплотнителем, препятствующим фильтрации через боковую поверхность. Здесь образец под вакуумом насыщается жидкостью, которая затем фильтруется через него при заданном перепаде давления p . Измерив расход Q по формуле 12.3 определяют коэффициент проницаемости породы.

Для песчаных грунтов применяют формулу Хазена :

	k =	cde 2g	,	(12.11)
		v

где с – безразмерный коэффициент (в очень плотных песках – 8,5 × 10– 4, в песках средней пористости – 16×10–4), зависящий от пористости грунта, dэ – эквивалентный диаметр частиц [7, 10].

12.2 Основные законы фильтрации за границами применимости закона Дарси

Закон Дарси имеет очень широкую область применения и по праву считается основным законом фильтрации. Вместе с тем существуют условия, при которых закон Дарси нарушается, причем имеют место верхняя и нижняя границы его использования. Верхняя граница применения закона Дарси проявляется в породах высокой проницаемости при больших скоростях фильтрации. Природа ее связана с существенным проявлением инерционных и пульсационных сил, которые пропорциональны квадрату скорости фильтрации. Исходя из принципа независимости действия вязкого трении и пульсационных сил, можно предполагать, что наиболее достоверной формой основного закона фильтрации в этом случае является двучленная зависимость, предложенная в качестве общего закона фильтрации Ф. Форхгеймером и в дальнейшем обоснованная рядом теоретических и экспериментальных исследований:

I = av + bv2 .

(12.12)

Достоинством двучленной зависимости является ее универсальность, поскольку она охватывает предельные условия: наступление ламинарного режима при малых скоростях фильтрации,

98

когда член bv2 становится пренебрежимо малым по сравнению с av, и турбулентного режима при весьма больших скоростях фильтрации, когда можно пренебречь линейным членом по сравнению с квадратным. В этом смысле такая зависимость гораздо лучше используемой иногда степенной зависимости вида I = аvn при 1 ≤ п ≤ 2, которая, может примениться лишь в ограниченных пределах. Поскольку к тому же не имеется фактических доказательств сравнительных достоинств степенной зависимости по отношению к двучленной, то ее использование для пористой среды нельзя считать оправданным.

В зависимости 12.12 можно считать а=1/k, где k – «истинный» коэффициент фильтрации, характеризующий проницаемость при линейном законе фильтрации, тогда эту зависимость удобно представить в виде:

I= v (1 - α нv)/k,			(12.13)
где α н – коэффициент нелинейности фильтрации, который можно
определять по формуле:
α н= α p		× vg ,	(12.14)
	k

по опытным данным для песков α =0,1-0,3.

Параметр р по данным различных авторов, представляется выражениями, приведенными ниже:

С.Эргун: р = 0,14/n3/2;

С.Ирмей: р = 0,045/n3/2;

Ф. Энгелунд–В. М. Шестаков: p = 0,09 / n2 (1− n) ; Дж. Уорд: р = 0,55.

При допустимой погрешности в расчетах ( ε доп) критическая скорость фильтрации vкр, определяющая верхнюю границу применимости закона Дарси, получается из условия:

vкр =	ε доп	=	ε доп		vкр .
				vg / k		(12.15)
	α		p

Расчеты по последней формуле свидетельствуют о том, что нарушения линейного закона фильтрации могут иметь место лишь в высокопроницаемых породах в зоне резкой интенсификации фильтрационного потока, т.е. в условиях, встречающихся в гидрогеологической практике довольно редко; наступление же

99

турбулентного режима для натурных условий вообще нереально. Поэтому необходимость использования двучленного закона фильтрации возникает сравнительно редко и в каждом случае требует специального обоснования.

Гораздо больший принципиальный и практический интерес представляет анализ аномалий основного закона фильтрации, возникающих при малых скоростях фильтрации, характерных для слабопроницаемых пород. Природу этих аномалий связывают с влиянием сил молекулярного взаимодействия частиц воды и породы. В работах И. Ф. Бондаренко и С. В. Нерпина объяснение таких аномалий основывается на представлениях о вязко-пластическом характере течения воды в ультратонких поровых каналах. Рассматривая для анализа закономерностей вязко-пластического режима фильтрации простейшую модель пористой среды, состоящую из одинаковых капиллярных трубок с радиусом rТ, можно показать, что в этом случае вязкое течение начинается при градиенте напора Iо, определяемом по формуле:

I0 =	2τ 0	,	(12.16)
	ρ grT
где τ 0 – начальное сопротивление сдвигу в жидкости, которое, по
данным Н. Ф. Бондаренко, имеет порядок τ 0 =10-4 МПа; ρ			– плотность

воды; g – ускорение свободного падения.

При I >Iо основной закон фильтрации описывается уравнением:

V = k[I - 4 / 3× I0 + I0 / 3× (I0 / I )3 ].

(12.17)

При больших градиентах, когда I>>I0, этот график имеет линейную асимптоту:

V = k[I - 4 / 3× I0 ] .

(12.18)

Значения начальных градиентов в песках имеют порядок I0 = 10–3, а в глинах – до 1, в торфах до 15. Такие величины, несомненно, имеют реальную значимость, так что в природных условиях проявления вязкопластического течения, по-видимому, требуют тщательного анализа. Важно учитывать, что вязко-пластическое течение имеет релаксационный характер, обусловливающий возможность течения в пластической области I < I0, однако эффективная проницаемость породы здесь будет уже значительно меньше.

100

Рис. 12.2. Зависимость скорости фильтрации от гидравлического градиента

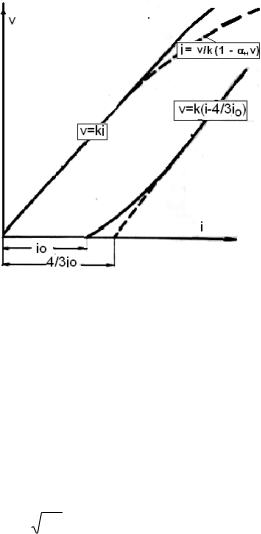
Анализируя графики основного закона фильтрации рис. 12.2 можно сделать вывод, что их области имеют относительно локальный характер по сравнению с областью применимости этого закона.

Поэтому при дальнейших обоснованиях закономерностей динамики подземных вод за основу будет приниматься, как правило, закон Дарси, а случаи его нарушения будут специально оговариваться.

Природа фильтрационных аномалий при ультрамалых скоростях фильтрации еще встречает различные толкования, причем имеются и негативные

данные о реальном проявлении начального градиента фильтрации. Граница перехода линейной фильтрации к нелинейной

определяется критическим значением числа Рейнольдса. Расчетные формулы для его определения имеют более сложный, чем в трубной гидравлике, вид, так как они должны учитывать и характеристики пористой среды. Из формул для Re, предложенных разными авторами,

наиболее употребительная формула Щелкачева:
Re = 10v kρ (е1.2 μ ) ,	(12.19)

где kп, е – коэффициенты проницаемости и пористости породы. Критические значения числа Рейнольдса для этой формулы

получены путем анализа экспериментальных данных: Reкр = 0,0324÷14 (меньшие критические значения соответствуют сцементированным породам, например песчаникам, большие – рыхлым пескам [7].

12.3. Простейшие случаи установившейся напорной фильтрации несжимаемой жидкости

Геометрия фильтрационных потоков воды, нефти и газа в реальных пластах может быть очень сложной: границы водонефтяного или водногазового контактов бывают самой причудливой формы, пласты часто имеют переменную по простиранию толщину, месторождения воды,

101

Рис. 12.3. Фильтрация жидкости в

Рис. 12.3.

прямолинейном пласте

нефти или газа разрабатываются десятками и сотнями скважин, которые могут вскрывать пласт не на всю его толщину (так называемые несовершенные по степени вскрытия скважины),

и т.д. Все это усложняет картину фильтрации и с трудом поддается учету. Вот почему при изучении реальных явлений происходящих в пластах, необходимо предварительно рассмотреть простейшие

фильтрационные потоки, из которых, как из элементов затем можно составить модели более сложных явлений.

Параллельно-прямолинейная фильтрация. Рассмотрим случай фильтрации жидкости в прямолинейном пласте (рис. 12.3). Пусть имеется пласт в форме параллелепипеда длиною L, шириною (в плане) В и толщиною h c непроницаемой кровлей и подошвой. На левой границе пласта, принимаемой за контур питания, давление рк, на правой, называемой галереей -рr Контуром питания будем называть изобарическую (с одинаковым в любой точке приведенным давлением, в данном случае pк) поверхность, галереей – условный вертикальный срез пласта, нормальный к линиям тока. За контур питания может быть принято любое живое сечение пласта, где давление известно и при фильтрации считается постоянным). Давлениям рк и рr соответствуют напоры Hк и Нr . Так как площадь фильтрации (w=Bh) постоянна по длине пласта, линии тока жидкости будут параллельны друг другу, а поля скоростей и приведенных давлений для любого горизонтального параллельного линиям сечения пласта будут одинаковыми (поперечных перетоков жидкости в нем нет). Такую фильтрацию называют прямолинейно-параллельной. Она происходила в опытах Дарси. (Напомним, что приведенные давления не зависят от положения пласта в пространстве).

Следовательно, расход (называемый дебитом) галереи по формуле

Q =	k		( pk −	pr )	Bh .	(12.20)
	μ		l

Скорость фильтрации, одинаковая для любого живого сечения пласта, определяется по выражению:

102

v =	k		( pk −	pr )	.	(12.21)
	μ		l

Возьмем параллельное галерее произвольное живое сечение пласта, находящееся от нее на расстоянии x, давление в котором равно р, а напор Нх. Приняв его за контур питания, запишем закон Дарси и выразим из него р:

P = pr +	Qμ x	.	(12.22)
	(kBh)

Подставив в это выражение значение Q из формулы 12.20, получим закон распределения давления по длине пласта:

	P = pr +	( pk − pr )	x .	(12.23)
		L

Линия падения давлений, следовательно, и соответствующих им напоров Н = ρpg , представляет собой прямую.

При разработке месторождений примером фильтрации, близкой к прямолинейно-параллельной, служит фильтрация в полосовой залежи, эксплуатирующейся прямолинейной цепочкой скважин. Плоскорадиальная фильтрация. Рассмотрим другой простейший случай фильтрационного потока плоско-радиальную фильтрацию несжимаемой жидкости. Пусть скважина расположена в центре кругового пласта толщиной h (рис. 12.4). Обозначим радиус контура питания Rк, радиус скважины rс, давление на них соответственно pк и рc. Пока скважина не эксплуатируется в любой точке пласта давление pк и соответствующий

ему статический уровень Hk = ρpgk . Для того, чтобы жидкость притекала к скважине, необходимо снизить давление на забое (нижней точке) рс, т.е. создать условие рк > рс (или Нк > Нс, где Нс = ρpgc ) – динамический

уровень жидкости в скважине). Если при этом динамический уровень окажется больше глубины скважины, она будет фонтанировать, т.е. жидкость сможет поступать на поверхность земли только за счет затрат пластовой энергии (гидростатической напора). Если Нс меньше глубины скважины, добывать жидкость можно только за счет внешних источников энергии (например насосами). Линии тока жидкости в

103

рассматриваемом случае направлены от контура питания к скважине по радиусу пласта, а поля скоростей фильтрации и давлений для любого его горизонтального сечения одинаковы. Такую фильтрацию называют плоско-радиальной.

Мысленно выделим элементарную струйку жидкости вдоль радиуса (на плане эта струйка заштрихована). Так как поперечные струйки малы, движение в ней можно считать параллельнопрямолинейным. На бесконечно малом перемещении (dr) падение давления вдоль струйки будет dр. Подставив в выражение вместо длины перемещения l величину dr, а вместо падения давления р величину dр получим закон Дарси в дифференциальной форме:

Рис. 12.4. Плоско-радиальная фильтрация жидкости

v =	k δ p	,	(12.24)
	μ δ r

δ р

где δ r – градиент давления.

Скорость фильтрации V и давление р для точек пласта, отстоящих на одинаковых расстояниях r от его центра в силу симметрии будут одинаковыми. Объемный расход жидкости через произвольное живое сечение пласта w(r) (в виде боковой поверхности цилиндра радиусом r и высотой h) составит:

	Q=vw(r)=	k dp		π rh .	(12.25)
		μ dr

Разделив переменные и подставив пределы интегрирования для р от pc до pk, а для r от rс до Rk, получим:

Rk		pk
Q ò dr/r=	2π kh	ò δπ.	(12.26)
	μ
rс		pc

104

После интегрирования:

æ

Rk

ö

2π kh

( p

)

Q lnç

÷

=

k

-

p

c

.

(12.27)

r

ç

÷

μ

è

c

ø

Решив последнее выражение относительно Q, окончательно имеем

Q =	2π kh	( pk − pc )				,
	μ	æ	R	k	ö		(12.28)
		lnç			÷
			r
		ç			÷
		è	c		ø

где разность давлений рк –рс называют депрессией. Выражение, являющееся законом Дарси для плоско-радиальной фильтрации, называют формулой Дюпюи, которая считается основной при расчетах, связанных с эксплуатацией водяных артезианских скважин, а также нефтяных месторождений. Формула может использоваться и для определения дебита нагнетательных скважин, используемых при заводнении пластов. В этом случае в числителе вместо депрессии, записывается pс–pк , так как рс> рк.

В формуле Дюпюи значение Rк, находится под логарифмом, поэтому ошибка в его определении незначительно сказывается на дебите. Обычно за Rк, (сели скважина одна) принимают расстояние от скважины до границы водонефтяного контакта, а если пласт разрабатывается большим числом скважин, то за Rк принимают половину расстояния между ними. Приняв за Rк произвольный радиус r а за рк соответствующее радиусу давление в пласте р, разрешим формулу Дюпюи относительно p:

			Qμ	æ	r	ö	(12.29)
p = p		+		ln ç		÷
			2π kh		r
	c			ç		÷ .
				è	c ø

Заменив Q в выражении 12.29 на полученное из выражения 12.28 имеем:

			( pk - pc )				æ	r	ö
p = p		+					ln ç		÷
			æ	R		ö		r
	c				k		ç		÷
			lnç			÷	è	c ø .		(12.30)
				r
			ç			÷
			è	c		ø

Из уравнения видно, что закон распределения давлений (а, следовательно, и динамических напоров) при плоско-радиальной фильтрации логарифмический. Поверхность, образующуюся от

105

вращения логарифмической пьезометрической линии, соединяющей динамические уровни, называют воронкой депрессии (рис. 12.4)

Из анализа формулы или рассмотрения воронки депрессии видно, что наибольшие потери давления (или соответствующие им потери напора) происходят в призабойной зоне. Это объясняется тем, что при постоянстве расхода (жидкость несжимаема) для любой цилиндрической поверхности радиуса r (Rк,<r<rc) максимальная скорость фильтрации будет в зоне малых r. А при фильтрации, также как и при движении жидкости в трубах, с ростом скорости растут и потери давления.

В промысловых условиях для повышения дебита скважин проницаемость призабойной зоны стремятся увеличить. Для этого проводят гидравлические разрывы пласта, обработку такой зоны кислотой (если пласт состоит из карбонатных пород) и другие технологические операции, облегчающие приток к скважинам. По формуле можно определить давление р в любой точке пласта, отстоящей от скважины на произвольном расстоянии r.

Полученные формулы справедливы для гидродинамически совершенных скважин, т.е. скважин, вскрывших пласт на всю его глубину и не отделенных от него обсадной колонной. Если пласт вскрыт не на всю глубину, скважина называется несовершенной по степени вскрытия, если имеется обсадная колонна с перфорированными отверстиями – несовершенной по характеру вскрытия. Возможны и оба вида несовершенства.

Несовершенные скважины дают, как правило, меньший дебит из-за возросшего сопротивления при фильтрации в призабойной зоне. Исключение составляют случаи, когда при перфорации (например, пескоструйной), образуются в пласте каналы, облегчающие приток жидкости.

Несовершенство скважин может быть учтено введением в формулу так называемого коэффициента

дополнительного фильтрационного cопротивления С, определяемого по специальным формулам или графикам, в этом случае формула Дюпюи принимает вид:

Q =	2π kh	( pk -			pc )
	μ	æ	R	k	ö
		lnç			+ C ÷ .		(12.31)
			r
		ç			÷
		è	c		ø		Рис. 12.5. График для определения
							Рис. 12.5.
							коэффициента С

106