Конспект лекций Высшая математика (Басканова)

x x t ,y y t

149

x x t ,

– функция одной переменной; y y t , – функция двух пе-

z z t

ременных.

Исключая параметр, можно получить функцию явно или неявно заданную.

x acost,	– параметрически заданная функция одной пере-
Пример.
y asin t
		2	a	2	cos		2	t,
	x
менной. Исключим параметр t :			a2 sin2 t,
	y2
тогда x2 y2 a2 cos2 t sin2 t x2 y2						a2 x2 y2 a2 0 – неявно за-

данная функция одной переменной.

Преимущества аналитического способа задания функции заключа-

ются: – в сжатости, компактности задания;

– в возможности применить к данной функции аппарат математического анализа, поскольку он наилучшим образом приспособлен к аналитической форме задания функций.

II. Графический способ задания функции состоит в построении графика этой функции.

Определение. Графиком функции называется геометрическое место точек, координаты которых удовлетворяют уравнению

		y					y f x z f x; y .
							Графиком функции одной переменной y f x
							является линия на плоскости.
		0			1
							x		x,	если x 0,
–1
		–1					Пример. Функция y				изо-
									2x,	если x 0
								x2

	рис. 2.2.3	бражена в виде графика (рис. 2.2.3).
		Графиком функции двух переменных z f x; y
	z	является поверхность в трехмерном пространстве.
		Пример. Графиком функции z 1 x2 y2

1является поверхность второго порядка – эллиптический параболоид (см. рис.2.2.4).

Кграфику функции не может быть непосред-

	–1	1	y ственно применен аппарат математического анали-
	1		за. Наряду с этим недостатком, график функции об-
x	рис. 2.2.4		ладает весьма важным преимуществом – наглядно-
			стью, что делает его чрезвычайно полезным при

150

изучении функции y f x .

III. Табличный способ задания функции состоит в перечислении значений независимой (независимых) переменной (переменных) и соответствующих им значений функции, с последующим занесением их в таблицу:

y f x

Таблица 2.2.1

x

x1

x2

…

z f x; y

y

f x1

f x2

…

Таблица 2.2.2

x

x1

x2

x3

…

y

f x3 ; y1

y1

f x1; y1

f x2 ; y1

…

f x3 ; y2

y2

f x1; y2

f x2 ; y2

…

…

Все вышеприведенные определения, относящиеся к случаю функции двух независимых переменных, без существенных изменений переносятся на случаи функции многих независимых переменных. Заметим только, что геометрическая иллюстрация функций от n независимых переменных при n 2 теряет наглядность.

2.2.4. Основные свойства функции

Изучить заданную функцию – это значит охарактеризовать ход её изменения при изменении независимой переменной.

Функции многих переменных, с которыми приходится иметь дело в инженерной практике, по своим свойствам, за исключением некоторых, мало отличаются от функций одной переменной. Поэтому рассмотрим основные характеристики поведения функции на примере функции одной переменной.

Определение. Нулем функции y f x называют такое значение x , при котором f x 0 .

В интервале положительного знака функции график расположен выше оси OX , в интервале отрицательного знака – ниже оси OX , в нуле

функции график пересекает ось OX .
Пример.	Найти	точки	пересечения	графика	функции
f x x3 7x2	10x с осью OX .

151

Решение: Ордината точки пересечения графика функции с осью OX равна нулю, т.е. y 0 . Значит абсцисса точки пересечения – есть нуль функ-

ции. Используя определение, получаем: f x 0 x3 7x2 10x 0 ;

x x2 7x 10 0,

x 0 , x2

7x 10 0,

1

x

7 49 40

x

2, x

5 .

2,3

2

2

3

Таким образом,

нули

функции:

y

x1 0, x2

2, x3 5,

а

точки

пересечения

графика

функции с

осью OX : A1 0;0 ,

1

A

A2

A3

A2 2;0 ,

A3 5;0 (см. рис.2.2.5).

Определение.

Промежутком, сим-

0

1

–1

2

5

метричным относительно начала коор-

f(x)=x3–7x2+10x

динат, называется промежуток, которому

вместе со значением x принадлежит проти-

рис. 2.2.5

воположное ему значение: x .

Определение. Функция

y f x , заданная на симметричном относи-

тельно начала координат промежутке, называется четной, если для любого значения x из этого промежутка выполняется равенство f x f x .

y

	y
–a	рис. 2.2.6	a	x

–a

0

a

График четной функции симметричен относительно оси OY (см. рис. 2.2.6).

Определение. Функция y f x , заданная на

симметричном относительно начала координат промежутке, называется нечетной, если для любого значения x из этого промежутка выполняется равенство f x f x .

График нечетной функции симметричен относительно начала координат (см. рис.2.2.7).

Сумма и разность двух четных (нечетных) функций есть функция четная (нечетная).

Произведение двух четных или двух нечет-

xных функций есть функция четная, а произведение четной функции на нечетную – нечетная функция.

	Пример. Функция f x	1 x2 – четная,
рис. 2.2.7	так как в области определения	D f 1;1 вы-

			152
полняется равенство	f x	1 x 2	1 x2 f x .		А функция f x x2		x
– ни четная, ни	нечетная,		так	как на	всей числовой		оси
f x x 2 x x2 x f x и		f x x2 x f x , где f x x2 x .
Определение. Функция		y f x		называется периодической, если су-
ществует число T 0	такое, что для любого значения x					из области опреде-
ления функции выполняется равенство				f x T f x ,		где T – наимень-

ший положительный период.

Если T – наименьший положительный период функции, то число kT , где k 1; 2; 3;... – также является периодом функции.

Пример.	Наименьшим положительным периодом функциЙ sin x и
cos x является	число T 2 : sin x 2 sin x, cos x 2 cos x , а для

функций tgx и ctgx это число T .

Из определения периодической функции следует, что её график будет «повторять» себя через промежуток равный по длине наименьшему положительному периоду T . Поэтому достаточно построить график такой функции

y

на

любом

промежутке

вида

2

a x a T a T x a .

Смещая постро-

1

енный

график вдоль

оси

OX

на отрезке

0

2

x длины

T ,

получим

график

функции

y f x .

рис. 2.2.8

Пример. График функции

y

y=f(x)

1,

если 2 x 0,

f x

1 x,

0 x 2

– периодиче-

f(x2)

если

f(x1)

ской, с наименьшим положительным перио-

дом T 4 (см. рис.2.2.8).

y f x на-

0 a

x1

x2

b

x

Определение.

Функция

зывается возрастающей

на

некотором

y

рис. 2.2.9

интервале, если большим значениям аргу-

мента

соответствуют

большие

значения

функции,

т.е. если x1 x2 ,

то

f x1 f x2

f(x1)

y=f(x)

(см. рис. 2.2.9).

y f x назы-

f(x2)

Определение. Функция

a

x1

x2

b

x

вается убывающей на некотором интервале,

рис. 2.2.10

если большим значениям аргумента соответ-

ствуют меньшие значения функции, т.е. если

x1 x2 , то

f x1 f x2

(см. рис.2.2.10).

153

Возрастающие и убывающие функции называются монотонными функциями. Интервал, на котором функция возрастает (убывает) называется

интервалом возрастания (убывания) функции или интервалом монотонности.

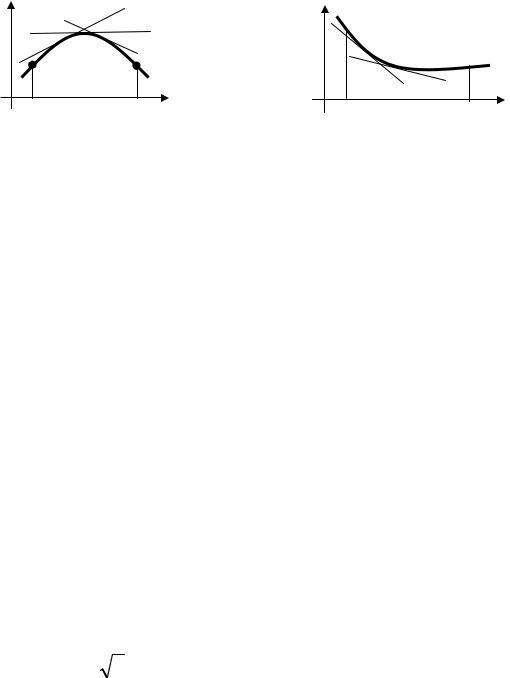
Определение. График функции y f x называется выпуклым (во-

гнутым) на некотором интервале, если касательная, проведенная к графику функции в любой точке с абсциссой из этого интервала, расположена выше (ниже) графика функции (см. рис. 2.2.11, 2.2.12).

y

y

				y=f(x)			y=f(x)
			0 a	b x	0	a	b	x
			рис. 2.2.11				рис. 2.2.12
			Определение.	Функция y f x	называется ограниченной, если су-
ществует такое число L 0 , что для всех x D f						выполняется неравенство
	f x		L .

График ограниченной функции лежит между прямыми y L и y L .

Определение. Значение функции, большее (меньшее) всех других её значений в некотором интервале, называется наибольшим (наименьшим)

значением функции в этом интервале.

Ограниченная на некотором отрезке функция принимает на этом отрезке свое наибольшее и наименьшее значения.

Определение. Пусть задана функция y f x с областью определения D и областью значений E . Если каждому значению y E соответствует единственное значение x D , то определена функция x y , обратная к функции y f x , с областью определения E и областью значений D .

Про функции y f x и x y говорят, что они являются взаимно обратными. Чтобы найти функцию x y достаточно решить уравнение f x y относительно x (если это возможно).

Примеры.

1.Для функции y 1 x обратной является функция x y 1.

2.Для функции y x2 на интервале 0; обратная функция сущест-

вует и имеет вид x y , а на интервале ; не существует, так как одному значению y соответствует два значения x .

154

Если необходимо построить графики взаимно обратных функций так, чтобы ось OX была осью аргумента, надо обозначить аргумент в обратной

функции через x , а функцию через y , т.е. функция примет вид y x . График обратной функции y x симметричен с графиком функции

y f x относительно биссектрисы первого и третьего координатных углов

(см. рис.2.2.13).

	y x2			Геометрически ясно,						что только моно-
y				тонная	функция имеет				обратную,		однознач-
		y x
				ную функцию.
											y y u
		y	x	Определение.				Пусть функция
1				определена		на	множестве			D , а	функция
				u u x на множестве D1 , причем для любого
0	1		x	x D1 ,	соответствующее значение U D . То-
	рис. 2.2.13			гда на	множестве			D1	определена		функция
				y y u x ,		которая			называется		сложной
функцией от x		(или суперпозицией заданных функций,								или функцией от
функции).
	Переменную u u x называют промежуточным аргументом слож-
ной функции.				tgx есть суперпозиция двух функций y 3 u и
	Пример. Функция y 3
u tgx .
	Сложная функция может иметь несколько промежуточных аргументов.
	Пример.	Функция	y ln2 3x 1 является					сложной функцией двух
промежуточных аргументов				y y u g x ,			где	y u2 ,		а промежуточные

аргументы: u ln g и g 3x 1.

2.2.5. Классификация функций. Основные элементарные функции, их свойства и графики

Функции одной переменной делят на два класса по области сущест-

вования.

Определение. Если областью существования функции	y f x слу-
жит множество натуральных чисел N , то функцию y f n	называют по-
следовательностью и обозначают xn , yn , zn и т. д.

155

Как правило, последовательность задают: формулой общего члена (например, xn : xn 3nn 1) или рекуррентно (например, yn : yn 3yn 2 2 yn 1 ,

т.е. через связь с предыдущими членами последовательности). Определение. Если областью определения функции y f x служит

один или несколько интервалов числовой оси OX , или вся числовая ось, то функцию называют функцией непрерывного аргумента.

Косновным элементарным функциям относятся:

–степенная функция y xn , n R ;

–показательная функция y ax , a 0,a 1;

–логарифмическая функция y loga x , a 0,a 1;

– тригонометрические функции y sin x .

y cos x ,

y tgx , y ctgx ;

– обратнотригонометрические функции

y arcsin x , y arccos x ,

y arctgx ,

y arcctgx .

Графики и наиболее важные свойства основных элементарных функ-

ций приведены в таблице.

Таблица 2.2.3.

Основные элементарные функции

Функция

График

Свойства

y xn

n -четное

n -нечетное

n N

y

y=x3

D f R

D f R

y=x4

y

E f 0;

E f R

Четная.

Нечетная.

x

Возрастает

Возрастает

1

0

при

при

x

x 0;

x ;

-1

1

.

Убывает при

x ;0 .

y

n

x

y

y

n -четное

n -нечетное

D f 0;

D f R

n N

y 3

E f 0;

E f R

n 1

y x

2

x

1

1

x

Ни четная ни

Нечетная.

нечетная.

Возрастает

x

Возрастает

при

1

4

при

x ;

x 0;

156

y ax

y=ax

y

y=ax

D f R , E f R

a 0,

Ни четная ни нечетная.

0<a<1

a>1

a 1

Возрастает при x ; , если

1

a 1убывает x ; , ес-

-1 0 1

x

ли 0 a 1.

y loga x

y

D f 0; , E f R

a 0,

Ни четная ни нечетная.

a 1

y=logax,

Возрастаетx 0; , если

a>1

0

x

a 1.

1

y=logax,

Убывает x 0; , если

0<a<1

0 a 1

y cos x

y

D f R

y=cosx

E f 1;1

1

π

Четная.

Возрастаетx 2 n;2 n .

0

x

-2π

-π

-1

Убывает x 2 n; 2 n n Z .

Периодическая T 2 .

y sin x

y

y=sinx

D f R

1

E f 1;1

-π

π

Нечетная.

0

-

2π

2π x

-1

Возрастает x

2

2 n;

2

2 n .

x

3

Убывает

2 n;

2 n .

2

2

n Z .

Периодическая T 2 .

y tgx

y

D f

2

n;

2n

n .

y=tgx

E f R .

Нечетная.

-π

π

x

Возрастает x

n;

n .

2

2n

2

2

Периодическая T .

157

y ctgx	y
		y=ctgx
-π	π	x
	2
2

y arcsin x	y			y=arcsinx
		2
-1				1 x
	2
y arccos x			y	π

y=arccosx

-1

1

x

y arctgx	y
							y=arctgx
	2
				1			x
				2
y arcctgx
		y		π			y=arcctgx
				2
	0						x

D f n; n E f R

Нечетная.

Убывает x n; n . Периодическая T .

D f 1;1

E f ;2 2

Нечетная. Возрастает x 1;1 .

D f 1;1

E f 0;

Ни четная ни нечетная. Убывает x 1;1 .

.

D f R
			;
E f		2		2

Нечетная. Возрастает x ;

D f R

E f 0;

Ни четная, ни нечетная. Убывает x ; .

158

Определение. Функции, составленные из основных элементарных функций, называются элементарными, если удовлетворяют двум условиям: задаются одним аналитическим выражением в области определения; представляют результат конечного числа алгебраических операций и операций взятия функции от функции.

Примеры. Неэлементарными функциями могут служить следующие функции:

1.		1,	если x 2,	– функция в области определения задана дву-
	y	x,	если x 2
	3
мя аналитическими выражениями.
2.	y 1 x2 x3 x4 ... xn ... – формула, задающая функцию, со-

стоит из бесчисленного числа операций.

Элементарные функции разделяют на два класса: алгебраические и трансцендентные функции.

Определение. Функция называется алгебраической, если её значение можно получить, производя над независимой переменной конечное число алгебраических действий: сложений, вычитаний, делений и возведений в степень с рациональным показателем.

Среди алгебраических функций в свою очередь выделяют:

1. Рациональные функции, если среди алгебраических действий, производимых над независимой переменной, отсутствует операция извлечения корня:

–

многочлены

P

x a xn a

xn 1

... a x2

a x a

,

например,

x 7x3 8x2 3x 1.

n

n

n 1

2

1 0

P

3

– дробно-рациональные функции (отношение многочленов)

P

x

a

xm a

xm 1 ... a x2

a x a

,

m

m

m 1

2

1

0

Q

x

b xn b

xn 1

... b x2 b x b

n

x

n

n 1

2

1

0

например

P2

3x2 5x

.

Q

x

2x 9

1

2. Иррациональные функции, если среди алгебраических действий, производимых над независимой переменной, есть операция извлечения кор-

ня, например: y x3 1 ; y 3 x 5 x2 . x 1

Определение. Функции, не являющиеся алгебраическими, называются

трансцендентными.

Ктрансцендентным функциям относятся:

–показательная;

–логарифмическая;