
- •Первообразная. Неопределенный интеграл и его свойста.
- •Интегрирование заменой переменной.
- •Определение рациональной функции. Разложение правильной рациональной дроби на сумму простейших дробей.
- •Интегрирование простейших дробей первого и второго типов.
- •Интегрирование дробей вида и .
- •Интегрирование иррациональных функций вида
- •Интегрирование иррациональных функций. Первая подстановка Эйлера.
- •Интегрирование иррациональных функций. Вторая подстановка Эйлера.
- •Определенный интеграл. Определение. Физический и геометрический смысл.
- •Свойства определенного интеграла. Теорема о среднем.
- •Производная интеграла с переменным верхним пределом.
- •Абсолютно сходящиеся интегралы первого рода. Теоремы о сходимости.
- •Несобственные интегралы второго рода. Теоремы сравнения.
- •Абсолютно сходящиеся интегралы второго рода. Теоремы о сходимости.
- •Непрерывность функции нескольких переменных
- •27. Частные производные. Геометрический смысл частных производных функции двух переменных.
- •28. Дифференцируемость функции нескольких переменных.
- •29. Необходимые условия дифференцируемости функции. Достаточное условие.
- •30. Полные дифференциалы. Частные дифференциалы.
- •31. Производные сложных функций.(правильное)
- •32. Неявные функции. Теорема о существовании неявной функции.
- •33. Касательная плоскость и нормаль к поверхности.
- •34. Производные высших порядков.
- •35. Дифференциалы высших порядков.
- •37. Экстремум функции нескольких переменных. Необходимое условие существования экстремума.
- •38. Достаточное условие экстремума функции двух переменных.
- •39. Условный экстремум.
- •40. Производная поля по направлению. Градиент функции.
- •41. Двойной интеграл. Определение и основные свойства.
- •42. Сведение двойного интеграла к повторному (случай прямоугольника).
- •43. Сведение двойного интеграла к повторному (случай произвольной области).
- •46. Двойной интеграл в полярных координатах.
- •47. Тройной интеграл. Свойства тройных интегралов.
- •48. Вычисление тройного интеграла в декартовых координатах.
- •49. Вычисление тройного интеграла в цилиндрических координатах.
- •50. Вычисление тройного интеграла в сферических координатах.
- •51. Криволинейные интегралы первого рода. Определение. Свойства. Вычисления.
- •52. Криволинейные интегралы второго рода. Вычисления.
- •53. Формула Грина.
- •54. Поток вектора через поверхность. Его свойства.
- •55. Поток вектора через незамкнутую поверхность
- •56. Поток вектора через замкнутую поверхность. Теорема Гауса-Остроградского.
- •57. Дивергенция векторного поля.
- •58. Циркуляция векторного поля. Ротор вектора.
50. Вычисление тройного интеграла в сферических координатах.
|
|
Если область интегрирования при вычислении тройного интеграла представляет собой тело, ограниченное сферой или некоторой ее частью, целесообразно перейти к сферическим координатам. |
Формулы перехода
от декартовых координат x,
y
и z
к сферическим координатам r,
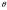 и
и
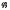 исходя из приведенного чертежа, имеют
вид:
исходя из приведенного чертежа, имеют
вид:
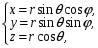 (25.5)
(25.5)
где
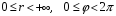 (или
(или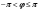 ),
),

Формула замены переменных в тройном интеграле при переходе к сферическим координатам имеет вид:
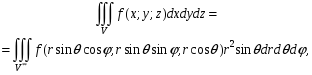 (25.6)
(25.6)
где
 – область в сферической системе
координат, соответствующая области
V
в декартовой системе координат;
– область в сферической системе
координат, соответствующая области
V
в декартовой системе координат;
f(x; y; z) – функция, непрерывная в этой области.
51. Криволинейные интегралы первого рода. Определение. Свойства. Вычисления.
Пусть на плоскости
xOy
задана гладкая незамкнутая кривая L
с началом в точке A
и концом в точке B,
не имеющая самопересечений. Допустим,
что на этой кривой определена непрерывная
функция
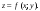 Разобьем указанную кривую L
произвольным образом на элементарные
дуги
Разобьем указанную кривую L
произвольным образом на элементарные
дуги
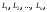 длины которых будем считать соответственно
равными
длины которых будем считать соответственно
равными
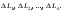 На каждой из элементарных дуг
На каждой из элементарных дуг
 выберем произвольную точку
выберем произвольную точку
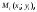
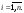 Обозначим через
Обозначим через
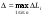 и составим интегральную
сумму
и составим интегральную
сумму
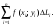 Устремим
Устремим
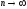 так, чтобы
так, чтобы
 Если существует предел интегральных
сумм, который не зависит ни от способа
разбиения кривой L
на части, ни от выбора точек
Если существует предел интегральных
сумм, который не зависит ни от способа
разбиения кривой L
на части, ни от выбора точек
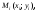 то этот предел называется криволинейным
интегралом 1-го рода от
функции f(x; y)
вдоль кривой L:
то этот предел называется криволинейным
интегралом 1-го рода от
функции f(x; y)
вдоль кривой L:
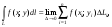 dl
называют дифференциалом
длины дуги,
а саму кривую L
– линией
интегрирования.
При этом говорят, что функция f(x; y)
интегрируема
по кривой
L.
dl
называют дифференциалом
длины дуги,
а саму кривую L
– линией
интегрирования.
При этом говорят, что функция f(x; y)
интегрируема
по кривой
L.
Если L – гладкая кривая в трехмерном пространстве без самопересечений, а f(x; y; z) – непрерывная функция в точках этой кривой, то криволинейный интеграл 1-го рода по этой кривой определяется равенством
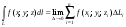 в случае существования
предела и при аналогичных плоской кривой
условиях.
в случае существования
предела и при аналогичных плоской кривой
условиях.
Если кривая L
представляет собой замкнутый контур
(т. е.
начало кривой и ее конец совпадают),
используют специальное обозначение:
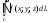 Достаточное
условие интегрируемости функции:
если функция определена и непрерывна
в точках гладкой, не имеющей самопересечений,
кривой, то она интегрируема по этой
кривой.
Достаточное
условие интегрируемости функции:
если функция определена и непрерывна
в точках гладкой, не имеющей самопересечений,
кривой, то она интегрируема по этой
кривой.
Если функции f(x; y), f1(x; y) и f2(x; y) интегрируемы по гладкой кривой L, то справедливы следующие свойства:
1) линейность:
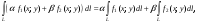 где
где
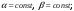
2) аддитивность:
если гладкая или кусочно-гладкая кривая
L
состоит из конечного числа гладких дуг
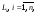 то
то
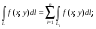 3) независимость
от направления пути интегрирования:
если кривая L
соединяет точки A
и B,
то
3) независимость
от направления пути интегрирования:
если кривая L
соединяет точки A
и B,
то
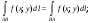
4) оценка модуля интеграла:
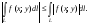
52. Криволинейные интегралы второго рода. Вычисления.
Пусть на плоскости xOy задана гладкая незамкнутая кривая L, и на этой кривой определена вектор-функция
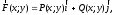
где P(x; y) и Q(x; y) – непрерывные функции.
Разобьем
указанную кривую L
произвольным образом на элементарные
дуги
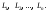 На каждой из элементарных дуг
На каждой из элементарных дуг
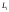 выберем произвольную точку
выберем произвольную точку
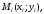
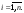
Составим произведение
значения функции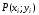 на длину проекции
на длину проекции
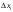 дуги
дуги
 на ось Ox
и произведение значения функции
на ось Ox
и произведение значения функции
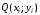 на длину проекции
на длину проекции
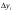 дуги
дуги
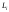 на ось Oy.
Запишем предельную сумму:
на ось Oy.
Запишем предельную сумму:

Обозначим
через
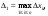 а через
а через
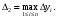 Устремим
Устремим
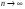 так, чтобы
так, чтобы
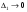 и
и
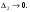 Если существует предел интегральных
сумм, который не зависит ни от способа
разбиения кривой L
на части, ни от выбора точек
Если существует предел интегральных
сумм, который не зависит ни от способа
разбиения кривой L
на части, ни от выбора точек
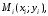 то этот предел
называется криволинейным
интегралом
2-го
рода
от функции
то этот предел
называется криволинейным
интегралом
2-го
рода
от функции
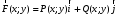 по координатам x
и y:
по координатам x
и y:
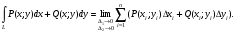
Если L
– гладкая кривая в трехмерном пространстве,
а
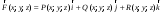 – вектор-функция, заданная на L,
причем P(x; y; z),
Q(x; y; z)
и R(x; y; z)
– непрерывные функции в точках этой
кривой, то в случае существования предела
и при аналогичных плоской кривой условиях
криволинейный интеграл 2-го рода по
координатам x,
y
и z
определяется равенством:
– вектор-функция, заданная на L,
причем P(x; y; z),
Q(x; y; z)
и R(x; y; z)
– непрерывные функции в точках этой
кривой, то в случае существования предела
и при аналогичных плоской кривой условиях
криволинейный интеграл 2-го рода по
координатам x,
y
и z
определяется равенством:
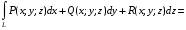
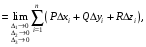
где в правой части
формулы
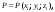
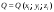 и
и
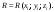
Если кривая L
представляет собой замкнутый контур
(т. е.
начало кривой и ее конец совпадают),
вводят понятие положительного
и отрицательного
направлений
обхода контура. Положительным
направлением обхода контура
называется
такое направление, при котором
линия
интегрирования обходится против хода
часовой стрелки. Противоположное ему
направление обхода контура называется
отрицательным.
При этом считают, что
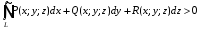 при положительном направлении обхода
контура L.
при положительном направлении обхода
контура L.
