
- •Первообразная. Неопределенный интеграл и его свойста.
- •Интегрирование заменой переменной.
- •Определение рациональной функции. Разложение правильной рациональной дроби на сумму простейших дробей.
- •Интегрирование простейших дробей первого и второго типов.
- •Интегрирование дробей вида и .
- •Интегрирование иррациональных функций вида
- •Интегрирование иррациональных функций. Первая подстановка Эйлера.
- •Интегрирование иррациональных функций. Вторая подстановка Эйлера.
- •Определенный интеграл. Определение. Физический и геометрический смысл.
- •Свойства определенного интеграла. Теорема о среднем.
- •Производная интеграла с переменным верхним пределом.
- •Абсолютно сходящиеся интегралы первого рода. Теоремы о сходимости.
- •Несобственные интегралы второго рода. Теоремы сравнения.
- •Абсолютно сходящиеся интегралы второго рода. Теоремы о сходимости.
- •Непрерывность функции нескольких переменных
- •27. Частные производные. Геометрический смысл частных производных функции двух переменных.
- •28. Дифференцируемость функции нескольких переменных.
- •29. Необходимые условия дифференцируемости функции. Достаточное условие.
- •30. Полные дифференциалы. Частные дифференциалы.
- •31. Производные сложных функций.(правильное)
- •32. Неявные функции. Теорема о существовании неявной функции.
- •33. Касательная плоскость и нормаль к поверхности.
- •34. Производные высших порядков.
- •35. Дифференциалы высших порядков.
- •37. Экстремум функции нескольких переменных. Необходимое условие существования экстремума.
- •38. Достаточное условие экстремума функции двух переменных.
- •39. Условный экстремум.
- •40. Производная поля по направлению. Градиент функции.
- •41. Двойной интеграл. Определение и основные свойства.
- •42. Сведение двойного интеграла к повторному (случай прямоугольника).
- •43. Сведение двойного интеграла к повторному (случай произвольной области).
- •46. Двойной интеграл в полярных координатах.
- •47. Тройной интеграл. Свойства тройных интегралов.
- •48. Вычисление тройного интеграла в декартовых координатах.
- •49. Вычисление тройного интеграла в цилиндрических координатах.
- •50. Вычисление тройного интеграла в сферических координатах.
- •51. Криволинейные интегралы первого рода. Определение. Свойства. Вычисления.
- •52. Криволинейные интегралы второго рода. Вычисления.
- •53. Формула Грина.
- •54. Поток вектора через поверхность. Его свойства.
- •55. Поток вектора через незамкнутую поверхность
- •56. Поток вектора через замкнутую поверхность. Теорема Гауса-Остроградского.
- •57. Дивергенция векторного поля.
- •58. Циркуляция векторного поля. Ротор вектора.
29. Необходимые условия дифференцируемости функции. Достаточное условие.
Необходимые условия:
Теорема 1: если
функция
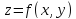 дифференцируема в точке, то она в этой
точке непрерывна.
дифференцируема в точке, то она в этой
точке непрерывна.
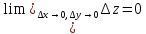
Теорема 2: если
функция
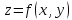 дифференцируема в точке (x,y),
то в этой точке она имеет частные
производные:
дифференцируема в точке (x,y),
то в этой точке она имеет частные
производные:
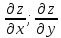
Достаточное
условие: если функция
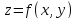 имеет частные производные в некоторой
окрестности точки и если производные
непрерывны в самой точке, то в этой точке
функция дифференцируема.
имеет частные производные в некоторой
окрестности точки и если производные
непрерывны в самой точке, то в этой точке
функция дифференцируема.
30. Полные дифференциалы. Частные дифференциалы.
Полный дифференциал:
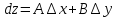 ;
;
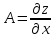 ;
;
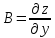 ;
;
 ;
;
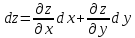 ;
;
ОПРЕДЕЛЕНИЕ: Частным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения ΔxZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. ΔyZ=f(y+Δy,x)-f(x,y).
Дифференциалы
независимых переменных х и у просто
равны их приращениям, т.е. dx=Δx, dy=Δy.
Частные дифференциалы обозначаются
так: dxZ -частный дифференциал по х, dyZ -
частный дифференциал по у. При этом:
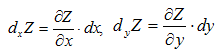
//31. Производные сложных функций.
Если
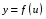 и
и
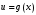 – дифференцируемые функции
своих аргументов, то производная сложной
функции
– дифференцируемые функции
своих аргументов, то производная сложной
функции
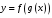 вычисляется по формуле
вычисляется по формуле
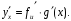 (11.8)
(11.8)
Обобщенная таблица производных
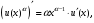 где
где
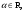 в частности:
в частности:

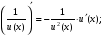
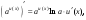 где
где
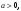
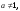 в частности,
в частности,
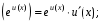
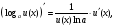 где
где
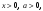
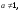 в частности,
в частности,
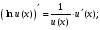
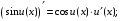
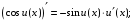
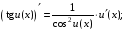
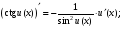
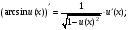
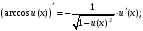
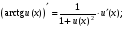
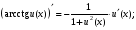
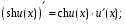
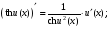
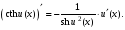
Если для функции
y = f(x)
существует обратная функция x = (y),
которая имеет производную
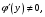 то верна формула
то верна формула
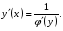
31. Производные сложных функций.(правильное)


32. Неявные функции. Теорема о существовании неявной функции.
Допустим, что
функция
![]() задана неявно уравнением
задана неявно уравнением
![]() (18.12)
(18.12)
и требуется найти
![]()
1-й способ. Если
практически возможно, из (18.12) выражают
явно
![]() через
через
![]() и дифференцируют.
и дифференцируют.
2-й способ.
Дифференцируют уравнение (18.12), считая
![]() и выражают затем
и выражают затем
![]()
3-й способ. Используют формулу
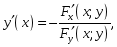 (18.13)
(18.13)
если
![]()
Способы 1–2 были рассмотрены в теории дифференцирования функции одной переменной и не всегда являются рациональными.
Производные неявной
функции
![]() порядка выше первого находят
последовательным дифференцированием
формулы (18.13), учитывая, что y
– функция от x.
порядка выше первого находят
последовательным дифференцированием
формулы (18.13), учитывая, что y
– функция от x.
Для нахождения
частных производных функции
![]() заданной неявно уравнением
заданной неявно уравнением
![]() (18.14)
(18.14)
используют формулы
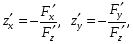 (18.15)
(18.15)
при условии, что
эти производные существуют и
![]()
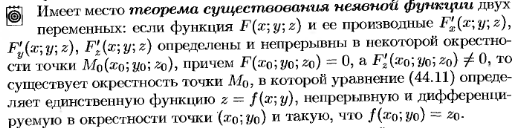
33. Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана уравнением
![]()
![]()
Тогда уравнение
касательной плоскости
в точке
![]() имеет вид:
имеет вид:
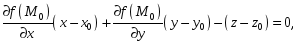 (18.16)
(18.16)
где
![]()
Нормалью
к поверхности в точке
![]()
![]() называется прямая, проходящая через
точку
называется прямая, проходящая через
точку
![]() перпендикулярно к касательной плоскости
в этой точке.
перпендикулярно к касательной плоскости
в этой точке.
Уравнение
нормали
к поверхности (18.16) в точке
![]() имеет вид:
имеет вид:
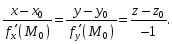 (18.17)
(18.17)
Если поверхность задана уравнением
![]() (18.18)
(18.18)
и в точке
![]() этой поверхности существуют частные
производные
этой поверхности существуют частные
производные
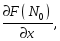
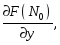
 не равные нулю одновременно, то уравнение
касательной плоскости к поверхности
(18.18) в точке
не равные нулю одновременно, то уравнение
касательной плоскости к поверхности
(18.18) в точке
![]() имеет вид:
имеет вид:
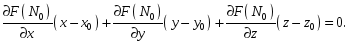 (18.19)
(18.19)
Уравнение нормали
к поверхности (18.18) в точке
![]() имеет вид:
имеет вид:
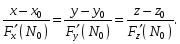 (18.20)
(18.20)
