11. Производная интеграла с переменным верхним пределом.

Пусть f(x) неопределенна на [a,b]. Возмем на нем произвольную т. x и рассмотрим определенный интеграл:

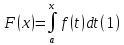
он сужествует для всех x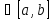 и является ф-ей своего верхнего предела.

Теорема:

Пусть f(x) – непрерывна на [a,b], тогда ф-я (1) имеет производную в любой т. x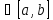, причем F’(x) = f(x).

Другими словами:

Производная от определенного интеграла по его верхнему пределу, равна значению подинтегральной ф-и в верхнем пределе.

Док-во:

Дадим аргументу x прирожение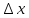, что (x + 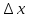)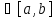, тогда ф-я F получить прирощение

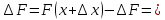
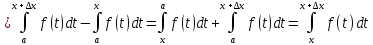
Применяем т. о Среднем значинии ф-ии:

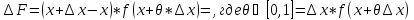
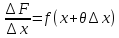
Переходим к lim при

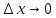
F’(x) =

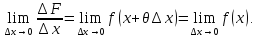
12. Формула Ньютона-Лейбница

Пусть ф-я f(x)-непрерывна на [a,b], а ф-я F(x) первообразная. Тогда:

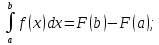
Док-во:

Рассмотрим ф-ю Ф(х) = 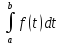. Эта ф-я является первообразной для f(x) на [a,b].

А любые две первообразные отличаются друг от друга на произвольную постоянную.

Ф(х) = F(x) + C, т.е.

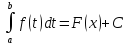
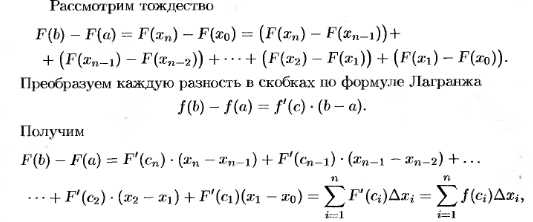
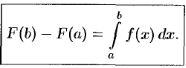
13. Замена переменной в определенном интеграле.

Пусть f (x) – непрерывная на отрезке [a; b] функция, а функция и ее производная непрерывны на отрезке где Тогда справедлива формула

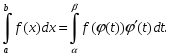
Доказывается по Ньютону-Лейбницу.

14. Интегрирование четных и нечетных функций.

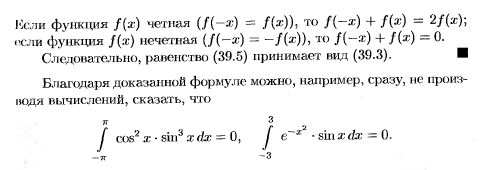
15. Определенный интеграл. Интегрирование по частям.

Пусть ф-я f(x) определена на отрезке [a,b]. Разобьем его на n-частей и составим интегральные суммы.

Число I называется пределом интегральных сумм:

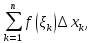
ф-ии f(x) на отрезке [a,b], если для любого ε > 0 существует δ>0, что для любого разбиения отрезка [a,b] на части с длинами 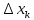< δ, неравенство:

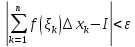
выполняются при любом выборе точек .

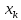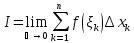
Если при любом разбиении отрезка [a,b] на части и при любом выборе точек 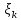на их интегральные суммы имеют один и тот же конечный предел, то этот предел называется определенным интегралом и обозначается:

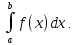
Интегрирование по частям

Пусть u(x) и v(x) – непрерывные функции, которые имеют непрерывные производные на отрезке [a; b]. Тогда справедлива формула интегрирования по частям:

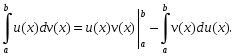
16. Нахождение площадей плоских фигур в прямоугольных координатах.

Пусть f(x) – непр. на [a,b] и a > b

1-й случай: 2-й случай:

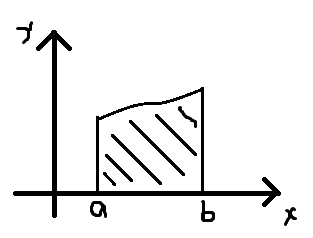
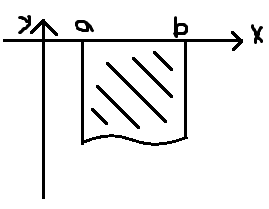
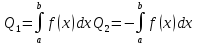
3-й случай: 4-й случай:

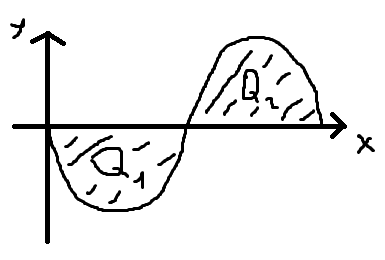
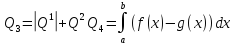
5-й случай:

Пусть кривая ab задана параметрическими уравнениями: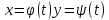

где 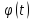и 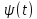непрер. Причем 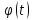имеет непрерывную производную

α <= t <= β.

Тогда:

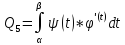
17. Нахождение площадей плоских фигур в полярных координатах.

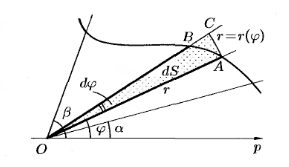
18. Вычисление объемов тел вращения.

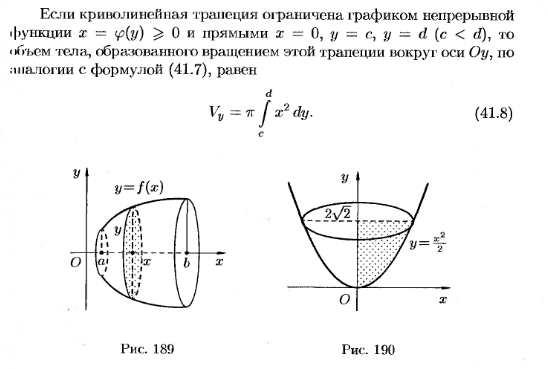
19. Длина кривой в прямоугольных координатах. Длина кривой заданной в параметрической форме.

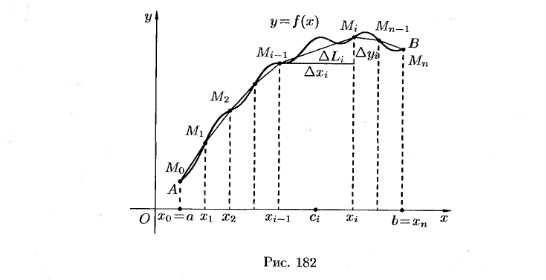
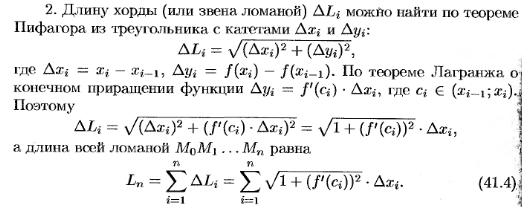
20. Длина кривой в полярных координатах. Дифференциал длины дуги кривой.

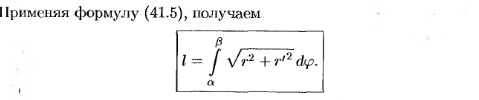
21. Несобственные интегралы первого рода. Теоремы сравнения.

Необходимым условием существования интеграла является ограниченность функции f(x). Поэтому интеграл от неограниченной функции в обычном смысле не существует. Однако, можно распространить определение определенного интеграла на неограниченные функции при помощи введения некоторых понятий.

Случай неограниченной области:

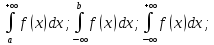
Пусть функция f(x) определена для всех x >= a и интегрируема на каждом конечном отрезке от a до b. Рассмотрим ф-ю аргумента b.

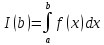
Если при b→+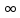 ф-я I(b) имеет конечный предел, то мы называем несобственный интеграл – сходящимся.

Если при b→+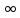 ф-я I(b) не имеет конечный предел, то мы называем несобственный интеграл – несходящимся.

Теоремы сравнения:

• Пусть на [a,b] при сущ. b > a, ф-и f(x) и φ(x) интегрир. И f(x) <= φ(x)

Тогда :1)

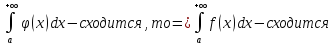
2)

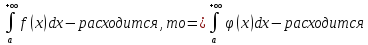
• Пусть ф-и f(x) и 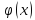непрерывны и неотриц. для всех x>=a, пусть 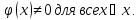Тогда если существует конечный предел 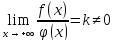, то 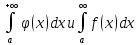сходятся или расходятся одновременно.

• Если существует такое число 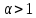, что для всех достаточно больших x: 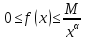, где М>0 и не зависит от х, то

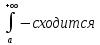
Если для Больших х: 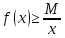, от .
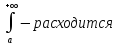