
- •Часть 2. Дифференциальные уравнения в частных производных первого порядка Лекция 11. Уравнения в частных производных первого порядка
- •11.1. Линейные и квазилинейные уравнения
- •11.2. Уравнения с переменными коэффициентами. Характеристики
- •11.3. Решение задачи Коши
- •12.2. Уравнение колебаний стержня
- •12.3. Уравнение теплопроводности и диффузии
- •12.4. Уравнения гидродинамики и звуковых волн
- •Лекция 13. Классификация уравнений в частных производных 2-го порядка, приведение их к каноническому виду и нахождение общего решения
- •Задания для самостоятельной работы
- •Лекция 14. Начальные и граничные условия
- •14.1. Начальные условия
- •14.2. Краевые задачи
- •Лекция 15. Решение задачи коши для волнового уравнения
- •15.1. Решение задачи Коши методом Даламбера
- •15.2. Решение задачи Коши для волнового уравнения методом Тейлора
- •Задания для самостоятельной работы
- •Лекция 16. Решение граничных задач волнового уравнения
- •16.1. Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны
- •16.2. Метод Фурье (метод разделения переменных) для уравнения вынужденных колебаний струны
- •Задания для самостоятельной работы
- •Лекция 16 (продолжение). Задача о напряженном состоянии элемента вооружения долота режущего действия
- •Лекция 17. Уравнения теплопроводности (диффузии) и методы их решений
- •17.1. Методы решения задачи Коши
- •Задания для самостоятельной работы
- •17.2. Методы решения граничных задач
- •Лекция 17 (продолжение). Расчет глубины промерзания связанных горных пород
- •Лекция 18. Стационарные уравнения. Уравнение лапласа и методы его решения
- •18.1.Задачи, приводящие к уравнениям эллиптического типа
- •18.2. Решения краевых задач для уравнения Лапласа в круге
- •Задания для самостоятельной работы
- •Лекция 19. Уравнение неразрывности и уравнения эйлера
- •19.1. Гипотеза сплошности
- •19.2. Установившееся и неустановившееся движения.
- •19.3. Уравнения гидродинамики и звуковых волн
- •19.4. Закономерности распространения плоских упругих волн
- •Лекция 20. Закономерности преломления и отражения плоских упругих волн на плоскости контакта твердых тел
- •Часть 4. Преобразование лапласа и его применение при решении дифференциальных уравнений Лекция 21. Преобразование лапласа
- •21.1. Преобразование Лапласа
- •21.2. Основные свойства преобразования Лапласа
- •21.3. Свертка функций
- •21.4. Оригиналы с рациональными изображениями
- •21.5. Нахождение оригинала по заданному изображению (когда оно рационально)
- •21.6. Оригиналы с изображениями, регулярными в бесконечности
- •Лекция 22. Практическое применение преобразования лапласа
- •22.1. Приложения к решению линейных дифференциальных уравнений с постоянными коэффициентами
- •22.2. Использование преобразования Лапласа при решении уравнений в частных производных
- •Лекция 23. Миграционная подмодель радиогеоэкологической модели подземного регионального хранилища радиоактивных отходов и ядерных материалов
- •Вопросы к экзамену по дисциплине: «Дифференциальные уравнения в горном деле»
Часть 2. Дифференциальные уравнения в частных производных первого порядка Лекция 11. Уравнения в частных производных первого порядка
11.1. Линейные и квазилинейные уравнения
Рассмотрим уравнение вида
![]() ,
(11.1)
,
(11.1)
в
котором х1,
х2,
…, хn
- независимые переменные функции u;
![]() -
частные производные функции u
по переменным
х1,
х2,
…, хn
.
-
частные производные функции u
по переменным
х1,
х2,
…, хn
.
Уравнение (11.1) называется уравнением в частных производных 1-го порядка. При этом, если уравнение (11.1) имеет вид
![]() ,(11.2)
,(11.2)
то оно будет называться линейным уравнением, а если уравнение (11.1) линейно только относительно частных производных и имеет вид
![]() ,(11.3)
,(11.3)
то
оно будет называться квазилинейным
уравнением. Уравнения (11.2) и (11.3) также
называются «n»-мерными
неоднородными
уравнениями, если функции
![]() в этих уравнениях будут равны нулю, то
тогда они будут называться однородными
уравнениями. Таким образом, «мерность»
уравнения определяется количеством
независимых переменных
х1,
х2,
…, хn.
в этих уравнениях будут равны нулю, то
тогда они будут называться однородными
уравнениями. Таким образом, «мерность»
уравнения определяется количеством
независимых переменных
х1,
х2,
…, хn.
Рассмотрим 2-х мерное квазилинейное однородное уравнение
![]() , (11.4)
, (11.4)
в котором для всех х и у выполняется неравенство
![]() . (11.5)
. (11.5)
Пусть
![]() ,
тогда уравнение (11.4) принимает вид
,
тогда уравнение (11.4) принимает вид
![]() , (11.6)
, (11.6)
Тогда
по условию (11.5) коэффициент
![]() ,
в силу того, что
,
не может быть равен нулю, следовательно,
может выполнятся только
,
в силу того, что
,
не может быть равен нулю, следовательно,
может выполнятся только
![]() или
или
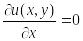 (11.7)
(11.7)
В уравнениях (11.7) переменная у присутствует лишь в качестве параметра. Зафиксируем ее значение, например, у = у1, тогда функция u1(x) = u(x,y1) и уравнением (7) принимает вид
![]() .
.
Решением этого уравнения будет функция
![]() .
.
Далее продолжим, зафиксируем у = у2, тогда функция u2(x) = u(x,y2) и уравнением (7) принимает вид
![]() .
.
Решением этого уравнения будет функция
![]() .
.
Продолжая далее, получим для у = уn,
![]() .
.
Константы С1, С2, …, Сn между собой никак не связаны. Мы видим, что они связаны лишь с переменной у и, если охватить все возможные значения константы, то решение уравнения (7) необходимо записать в виде
![]() . (8)
. (8)
Если предположить,
что
![]() ,
тогда уравнение (4) принимает вид
,
тогда уравнение (4) принимает вид
![]() ,
,
и
по условию (5) коэффициент
![]() ,
в силу того, что
,
не может быть равен нулю, следовательно,
может выполнятся только
,
в силу того, что
,
не может быть равен нулю, следовательно,
может выполнятся только
![]() или
или
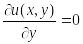 (9)
(9)
Далее поступая точно также, как мы поступали выше, только фиксируя значения х, получим
х = х1, тогда функция u1(у) = u(у,х1) и уравнением (7) принимает вид
![]() .
.
Решением этого уравнения будет функция
![]() .
.
Далее продолжим, зафиксируем х = х2, тогда функция u2(х) = u(у,х2) и уравнением (7) принимает вид
![]() .
.
Решением этого уравнения будет функция
![]() .
.
Продолжая далее, получим для х = хn,
![]() .
.
Константы С1, С2, …, Сn между собой никак не связаны. Мы видим, что они связаны лишь с переменной х и, если охватить все возможные значения константы, то решение уравнения (7) необходимо записать в виде
![]() . (10)
. (10)
11.2. Уравнения с переменными коэффициентами. Характеристики
Рассмотрим 2-х мерное квазилинейное однородное уравнение, котором коэффициенты при производных являются функциям х и у
![]() . (11)
. (11)
Введем новые переменные
![]() и
и
![]() . (12)
. (12)
и новую функцию
![]() (13)
(13)
Продифференцировав функцию (13) по х и у, получим
![]() и
и
![]() (14)
(14)
Подставив (14) в (11), получим

Предположим, что
коэффициент
![]() ,
тогда получим, что
,
тогда получим, что
![]() и решение этого уравнения по алгоритму,
рассмотренному ранее при решении
уравнения (4) принимает вид
и решение этого уравнения по алгоритму,
рассмотренному ранее при решении
уравнения (4) принимает вид
![]() , (15)
, (15)
но вид переменной ξ нам неизвестен и как, же ее найти? Рассмотрим систему обыкновенных дифференциальных уравнений
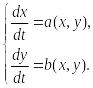 (16)
(16)
Для любого решения x(t), y(t) этой системы функция
F[x(t), y(t)] = const,
Называется общим
интегралом этой системы (16) и, если F
= const,
то производная от нее равна нулю
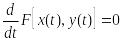 или раскрывая эту производную, получим
или раскрывая эту производную, получим
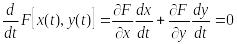 , (17)
, (17)
Исходя из того,
что в системе (16) -
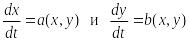 ,
то уравнение (17) можно записать в виде
,
то уравнение (17) можно записать в виде
![]() (18)
(18)
Анализируя уравнение (18) мы видим, что оно совпадает с исходным уравнением (11), следовательно, решениями уравнения (11) являются первые интегралы системы (16). Записав симметричную форму системы (16)
 ,
(19)
,
(19)
Эти уравнения называются уравнениями характеристик. Найдем интегралы этой системы. Первый интеграл очевиден
![]() .
.
Второй интеграл найдем из следующей комбинации
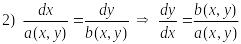 ,
,
интегрируя это уравнение, найдем
![]() .
.
Таким образом, общий интеграл уравнения (11) можно представить в виде
![]() , (20)
, (20)
а общее решение будет выглядеть как
![]() . (21)
. (21)
Интегралы С1 и С2 уравнения (19) называются характеристиками.
Пример 11.1. Найти общий интеграл и общее решение уравнения
![]()
▲ Запишем для этого уравнения систему (16)
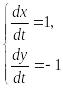
Далее запишем симметричную форму этой системы
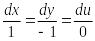 .
.
Первый интеграл очевиден
.
Второй интеграл найдем из следующей комбинации
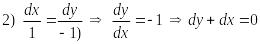 ,
,
интегрируя это уравнение, найдем
![]() .
.
Таким образом, общий интеграл исходного уравнения можно представить в виде
![]() ,
,
а общее решение будет выглядеть как
![]() .
.
Аналогичным образом решается уравнение
![]()
и его решение имеет вид
![]() .▲
.▲
Неоднородные уравнения решаются аналогичным образом.
Пример 11.2.
Найти общий интеграл и общее решение
уравнения
 .
.
▲ Запишем для него систему (16)
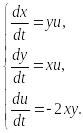
Далее запишем симметричную форму этой системы
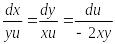 .
.
Первый интеграл очевиден
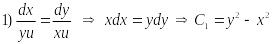 .
.
Второй интеграл найдем из следующей комбинации
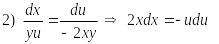 ,
,
интегрируя это уравнение, найдем
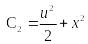 .
.
Таким образом, общий интеграл исходного уравнения можно представить в виде
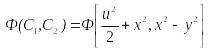 ,
,
а общее решение будет выглядеть как
![]() . ▲
. ▲
