11.3. Решение задачи Коши

Рассмотрим трехмерное квазилинейное однородное уравнение

(22)

Уравнение характеристик для него можно представить в виде

(23)

Эта система также называется системой дифференциальных уравнений векторных линий (т.е. линий касательная к которым в каждой точке имеет направление, совпадающее с направлением вектора

.

Поверхности, целиком содержащие векторные линии, имеющие хотя бы одну общую точку, называются векторными.

Если необходимо найти поверхность, проходящую через некую заданную линию, определяемую, например, уравнениями

(24)

то уравнение искомой поверхности определяется исключением x, y, z из системы

(25)

Которые должны одновременно удовлетворяться в точках заданной линии , через которую проводим характеристики, определяемые уравнениями

.

В результате чего получим уравнение

,

а искомым интегралом будет

.

Пример 11.3. Необходимо найти интегральную поверхность заданную уравнением

,

Проходящую через кривую, заданную уравнениями

.

▲ Запишем уравнение характеристик

.

Первый интеграл очевиден

.

Второй интеграл найдем из следующей комбинации

,

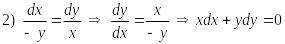интегрируя это уравнение, найдем

.

Составим систему (25)

Следовательно, т.к. , а , то уравнение искомой поверхности проходящей через заданную линию имеет вид

.▲

Задания для самостоятельной работы

Найти общий интеграл уравнений

11.1. . 11.2. . 11.3 .

11.4. . 11.5. .

11.6. . 11.7. .

11.8. . 11.9. .

11.10. .

11.11. .

Найти решения уравнений, удовлетворяющие начальным условиям

11.12. .

11.13. .

11.14. .

11.15. .

11.16. .

11.17. .

11.18. .

11.19. .

11.20. .

Часть 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА

Лекция 12. ОСНОВНЫЕ ВИДЫ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

12.1. Уравнение колебаний струны

Рассмотрим струну, под которой понимается тонкая нить, не сопротивляющаяся изгибу, длиной l . Пусть эта струна в плоскости (x,u) совершает малые поперечные колебания около своего положения равновесия, совпадающего с осью Ох, то есть все точки струны движутся перпендикулярно оси Ох. Обозначим через u(x,t) отклонение от положения равновесия точки струны с абсциссой х в момент времени t. Так как струна не сопротивляется изгибу, то ее натяжение в точке х в момент времени t направлено по касательной к струне в точке х. Любой участок струны (а,b) после отклонения от положения равновесия в предположении о пренебрежении величинами высшего порядка малости по сравнению с , не изменит своей длины

(12.1)

и, следовательно, величина натяжения будет постоянной Т₀, не зависящей от х и t, так как закон Гука гласит: изменение натяжения пропорционально изменению длины выделенного участка.

Составим уравнение движения струны. На элемент струны (х, х+Δх) действуют силы натяжения и внешняя сила , действующая на струну в точке х в момент времени t и направленная перпендикулярно оси Ох.

Сумма сил, действующих на струну, согласно закону Ньютона должна быть равна произведению массы элемента струны на его ускорение

, (12.2)

где - масса элемента струны (х, х+Δх); - единичный вектор, направленный вдоль оси u.

Проектируя векторное равенство (12.2) на ось u, получим

, (12.3)

но в рамках приближения

,

поэтому выражение (12.3) принимает вид

и при , получим

. (12.4)

Это и есть уравнение малых поперечных колебаний струны. Если F(x,t)0, то колебания струны будут вынужденными, а если F(x,t)=0, то колебания струны будут свободными.

Если , то уравнение (12.4) принимает вид

, (12.5)

где .

Уравнение (12.5) называется одномерным волновым уравнением.