
- •Часть 2. Дифференциальные уравнения в частных производных первого порядка Лекция 11. Уравнения в частных производных первого порядка
- •11.1. Линейные и квазилинейные уравнения
- •11.2. Уравнения с переменными коэффициентами. Характеристики
- •11.3. Решение задачи Коши
- •12.2. Уравнение колебаний стержня
- •12.3. Уравнение теплопроводности и диффузии
- •12.4. Уравнения гидродинамики и звуковых волн
- •Лекция 13. Классификация уравнений в частных производных 2-го порядка, приведение их к каноническому виду и нахождение общего решения
- •Задания для самостоятельной работы
- •Лекция 14. Начальные и граничные условия
- •14.1. Начальные условия
- •14.2. Краевые задачи
- •Лекция 15. Решение задачи коши для волнового уравнения
- •15.1. Решение задачи Коши методом Даламбера
- •15.2. Решение задачи Коши для волнового уравнения методом Тейлора
- •Задания для самостоятельной работы
- •Лекция 16. Решение граничных задач волнового уравнения
- •16.1. Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны
- •16.2. Метод Фурье (метод разделения переменных) для уравнения вынужденных колебаний струны
- •Задания для самостоятельной работы
- •Лекция 16 (продолжение). Задача о напряженном состоянии элемента вооружения долота режущего действия
- •Лекция 17. Уравнения теплопроводности (диффузии) и методы их решений
- •17.1. Методы решения задачи Коши
- •Задания для самостоятельной работы
- •17.2. Методы решения граничных задач
- •Лекция 17 (продолжение). Расчет глубины промерзания связанных горных пород
- •Лекция 18. Стационарные уравнения. Уравнение лапласа и методы его решения
- •18.1.Задачи, приводящие к уравнениям эллиптического типа
- •18.2. Решения краевых задач для уравнения Лапласа в круге
- •Задания для самостоятельной работы
- •Лекция 19. Уравнение неразрывности и уравнения эйлера
- •19.1. Гипотеза сплошности
- •19.2. Установившееся и неустановившееся движения.
- •19.3. Уравнения гидродинамики и звуковых волн
- •19.4. Закономерности распространения плоских упругих волн
- •Лекция 20. Закономерности преломления и отражения плоских упругих волн на плоскости контакта твердых тел
- •Часть 4. Преобразование лапласа и его применение при решении дифференциальных уравнений Лекция 21. Преобразование лапласа
- •21.1. Преобразование Лапласа
- •21.2. Основные свойства преобразования Лапласа
- •21.3. Свертка функций
- •21.4. Оригиналы с рациональными изображениями
- •21.5. Нахождение оригинала по заданному изображению (когда оно рационально)
- •21.6. Оригиналы с изображениями, регулярными в бесконечности
- •Лекция 22. Практическое применение преобразования лапласа
- •22.1. Приложения к решению линейных дифференциальных уравнений с постоянными коэффициентами
- •22.2. Использование преобразования Лапласа при решении уравнений в частных производных
- •Лекция 23. Миграционная подмодель радиогеоэкологической модели подземного регионального хранилища радиоактивных отходов и ядерных материалов
- •Вопросы к экзамену по дисциплине: «Дифференциальные уравнения в горном деле»
Лекция 23. Миграционная подмодель радиогеоэкологической модели подземного регионального хранилища радиоактивных отходов и ядерных материалов
В Горном институте КНЦ РАН разработана радиогеоэкологическая модель подземного регионального хранилища радиоактивных отходов (РАО) и ядерных материалов. Указанная модель создана для изучения экологической безопасности населения и окружающей среды региона. Радиогеоэкологическая модель позволяет, например, прогнозировать диффузионный перенос радиоактивности в гомогенном блоке вмещающего массива и адвективный перенос радионуклидов в приближении модели одиночной трещины.
Согласно основным международным и отечественным нормативным документам первоочередными задачами подземной изоляции радиоактивных отходов и отработавшего ядерного топлива являются:
- изоляция РАО от окружающей человека среды на длительные периоды времени, не перекладывая на будущие поколения ответственности за сохранение целостности систем захоронения и не создавая для них значительных ограничений вследствие наличия хранилища;
- обеспечение долговременной радиационной безопасности человека и окружающей среды в соответствии с действующими согласованными в международном порядке принципами радиационной безопасности.
В частности, ВАО и ОЯТ, имеющие значительные количества долгоживущих радионуклидов, предполагается размещать в глубоких геологических формациях. Долгосрочная безопасность такого объекта, как впрочем, и любого хранилища РАО, основывается на мультибарьерной защите и оценивается на основе показателей работы системы захоронения в целом. Причем поскольку долгосрочная безопасность захоронения ВАО и ОЯТ не может быть продемонстрирована непосредственным образом, приходится использовать методы, позволяющие выполнять долгосрочные прогнозные оценки. В частности, широкое распространение получили методы математического моделирования, аналитические способы решения дифференциальных уравнений с разнообразными граничными условиями и др.
Чаще всего оценка безопасности в конечном итоге сводится к вычислению доз облучения населения, получаемых за счет делокализации радионуклидов из хранилища в сферу жизнедеятельности человека. Рассчитанная величина мощности эффективной дозы сравнивается с верхним пределом мощности дозы для населения, установленным в стране для воздействия от объекта хранения/захоронения ядрных материалов. Далее предлагаются какие-либо решения, выполнение которых гарантирует безопасность захоронения отходов для населения и окружающей среды.
Необходимой стадией оценки безопасности является определение распространения радионуклидов в геологической формации с подземными водами и в биосфере. Основу этой стадии составляет расчет пространственно-временных полей концентрации отдельных радионуклидов. Необходимо оговориться, что последнее замечание в значительной степени справедливо для сценария нормальной эволюции хранилища, как методологии детерминистического подхода. В принципе, помимо сценария нормальной эволюции в оценках безопасности принято рассматривать и вероятностные (аварийные) сценарии, которые рассматриваются как некоторое отклонение от сценария нормальной эволюции (природные и техногенные дефекты, изменения климата, интрузия человека и др.).
При построении миграционной подмодели рассматривался сценарий нормальной эволюции, который можно определить как последовательность наиболее вероятных событий, происходящих после запечатывания хранилища. Считается, что компоненты системы захоронения, расположенные вне формы отходов, после запечатывания постепенно насыщаются подземными водами. В результате коррозии материала контейнера радионуклиды из матрицы получают возможность попасть в окружающий скальный массив. Далее предполагается, что в некоторой ограниченной зоне вблизи хранилища, расположенного в однородном блоке вмещающего массива, справедлива модель пористой среды (рис.22.1). На этом этапе перенос радионуклидов осуществляется только посредством диффузионного механизма с учетом эффектов сорбции-десорбции и радиоактивного распада. Начиная с некоторого расстояния, которое определяется размерами локальных и региональных нарушений, вмещающая порода рассматривается как трещиноватая среда, в которой перенос радионуклидов происходит с потоком подземной воды по трещинам. При этом основными механизмами переноса являются адвекция, дисперсия, включающая молекулярную диффузию и механическую дисперсию, а также сорбция-десорбция радионуклидов на минералах породы и радиоактивный распад. Далее радионуклиды, поступившие из трещин в водоносные горизонты или водоемы, разбавляются в больших объемах подземной воды водоносных горизонтов или поверхностных водоемов и, наконец, вместе с питьевой водой поглощаются населением, проживающим вблизи площадки захоронения.
Для воплощения рассматриваемого сценария в удобную для алгоритмизации форму приходится вводить некоторые модельные упрощения. В частности, предполагается, что:
- невозвратный железобетонный контейнер, предназначенный для захоронения РАО, и металлобетонный контейнер для ОЯТ способны предотвратить в течение некоторого начального периода времени контакт кондиционированной формы отходов с подземными водами. Сохранность этого защитного барьера определяет время начала высвобождения радионуклидов;
- кондиционированная матрица, представляющая собой цилиндр или прямоугольный параллелепипед, представляется матрицей сферической формы, что позволяет упростить вид аналитических решений. Содержание радионуклидов по объему матрицы предполагается равномерным;
- трещины заменяются прямолинейными параллелепипедами, которые характеризуются своими характеристиками, в т.ч. и гидрологическими;
- водоносные горизонты или поверхностные водоемы (например, озеро), для которых возможен учет водообмена, в процессе моделирования не изменяют своего объема и другие менее значимые модельные предположения.
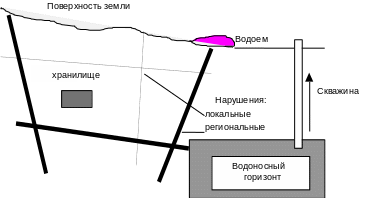
Рис.22.1. Модельное представление размещения хранилища, а также локальных и региональных нарушений (точечные и жирные линии)
Описание блоков миграционной подмодели.
В основу миграционной подмодели положены три взаимосвязанные модельных блока:
- блок диффузионной модели,
- блок модели адвекции-диффузии (модель одиночной трещины);
- блок модели биосферы.
Диффузионная модель описывает перенос радионуклидов в однородном вмещающем массиве с учетом источникового члена и радиоактивного распада посредством диффузионного механизма. Механизм высвобождения радиоактивности из отвержденной формы отходов может быть описан несколькими моделями. Остановимся на четырех, которые далее обсуждаются в порядке усложнения.
Модель №1.
Модель мгновенного растворения
предполагает мгновенное высвобождение
активности в поровую воду отвержденных
отходов -
![]() .
Типичными представителями элементов,
характеризующихся высокой растворимостью
являются цезий и йод. В контексте нашей
проблемы это могут быть, например,
изотопы -
.
Типичными представителями элементов,
характеризующихся высокой растворимостью
являются цезий и йод. В контексте нашей
проблемы это могут быть, например,
изотопы -
![]() и
и
![]() .
Строго говоря, данная модель может быть
применена не только к элементам с высокой
растворимостью. Но для этого необходимо
с учетом принимаемой модели адсорбции
проконтролировать полную активность
изотопа и предоставляемый отходам объем
порового пространства с численным
значением предела растворимости
элемента.
.
Строго говоря, данная модель может быть
применена не только к элементам с высокой
растворимостью. Но для этого необходимо
с учетом принимаемой модели адсорбции
проконтролировать полную активность
изотопа и предоставляемый отходам объем
порового пространства с численным
значением предела растворимости
элемента.
Модель №2.
Модель предела растворимости предполагает,
что концентрация радионуклидов на
границе раздела кондиционированной
формы отходов и скальной породы
лимитируется величиной элементной
растворимости его определенной химической
формы -
![]() .
Такая модель считается справедливой
для достаточно большого числа долгоживущих
радионуклидов, например, изотопы плутония
.
Такая модель считается справедливой
для достаточно большого числа долгоживущих
радионуклидов, например, изотопы плутония
![]() и урана
и урана
![]() .
.
Модель №3.
Простейшая модель выщелачивания, которая
предполагает знание помимо предела
элементной растворимости
еще и скорости выщелачивания активности
![]() из матрицы отвержденной формы отходов,
задаваемой в этой моделе постоянной
[2].
из матрицы отвержденной формы отходов,
задаваемой в этой моделе постоянной
[2].
Модель №4.
Двухкомпонентная модель выщелачивания,
которая предполагает наличие разных
скоростей выщелачивания активности из
матрицы отходов
![]() :
«быструю» компоненту с периодом
высвобождения порядка 1100 лет и «медленную»
компоненту с периодом высвобождения
около 22000 лет [3].
:
«быструю» компоненту с периодом
высвобождения порядка 1100 лет и «медленную»
компоненту с периодом высвобождения
около 22000 лет [3].
Следует отметить тот факт, что четвертая модель справедлива только для остеклованных РАО, а первые три модели, в принципе, могут быть использованы и для других форм отверждения отходов (цементная, битумная, керамическая матрицы).
Модель адвекции-диффузии
применяется для расчета переноса
радионуклидов по трещинам постоянной
гидравлической апертуры
![]() с потоком подземной воды. При этом
скорость ламинарного потока в трещинах
с потоком подземной воды. При этом
скорость ламинарного потока в трещинах
![]() определяется посредством известного
соотношения, справедливого для ламинарного
течения между параллельными пластинами
через коэффициент гидравлической
проводимости трещины
определяется посредством известного
соотношения, справедливого для ламинарного
течения между параллельными пластинами
через коэффициент гидравлической
проводимости трещины
![]() и градиент напора
и градиент напора
![]()
|
(23.1) |
где
![]() - плотность жидкости;
- плотность жидкости;
![]() - ускорение
свободного падения;
- ускорение
свободного падения;
![]() - динамическая
вязкость.
- динамическая
вязкость.
Биосферная модель описывает разбавление радионуклидов в биосфере и результирующие радиологические последствия при потреблении человеком загрязненной питьевой воды. Таким образом, рассматривается только внутреннее облучение населения через питьевую воду, как наиболее важную траекторию попадания радионуклидов в организм человека. Учитывая направленность пособия, эта модель подробно не описывается.
Диффузионная модель
В основе модели лежит обоснованное предположение, что отходы будут захоронены в стабильные геологические формации (типа гранита), не имеющие в области хранилища крупных протяженных трещин. Такое допущение позволяет рассматривать вмещающий массив в ограниченном масштабе площадки, как гомогенный, и моделировать перенос радионуклидов в этой области при доминирующем диффузионном механизме.
Единицей захоронения
считается один контейнер, содержащий
кондиционированные ВАО или ОЯТ. Время
разрушения контейнера (время начала
высвобождения радионуклидов)
![]() ,
после которого контейнер уже не
обеспечивает своей защитной функции,
оценивается через скорость коррозии
металла при его взаимодействии с
подземными водами. Известен целый ряд
исследований, посвященных определению
скорости коррозии металлических
контейнеров (стальных, медных) с РАО.
Все они свидетельствуют, что выбор
величины скорости коррозии на уровне
0,01 мм/год представляется разумным. При
вступлении кондиционированных отходов
в контакт с подземными водами начинается
высвобождение радионуклидов в результате
процесса выщелачивания.
,
после которого контейнер уже не
обеспечивает своей защитной функции,
оценивается через скорость коррозии
металла при его взаимодействии с
подземными водами. Известен целый ряд
исследований, посвященных определению
скорости коррозии металлических
контейнеров (стальных, медных) с РАО.
Все они свидетельствуют, что выбор
величины скорости коррозии на уровне
0,01 мм/год представляется разумным. При
вступлении кондиционированных отходов
в контакт с подземными водами начинается
высвобождение радионуклидов в результате
процесса выщелачивания.
В сферической системе координат управляющее дифференциальное уравнение, описывающее диффузионный перенос растворенной в воде порового пространства радиоактивности с учетом радиоактивного распада, а также типичные начальное и граничное (на бесконечности) условия, имеют вид:
, |
(23.2) |
для
|
(23.3) |
где - концентрация радиоактивного вещества, растворенного в воде порового пространства;
- постоянная распада;
![]() -
пространственная и временная координаты;
-
пространственная и временная координаты;
![]() - радиус контейнера
(источника);
- радиус контейнера
(источника);
 - наблюдаемый
коэффициент диффузии;
- наблюдаемый
коэффициент диффузии;
![]() - коэффициент
диффузии радионуклида по обводненному
поровому пространству породы, который
определяется посредством выражения
- коэффициент
диффузии радионуклида по обводненному
поровому пространству породы, который
определяется посредством выражения
![]() ;
;
![]() - молекулярный
коэффициент диффузии ионов в свободной
воде;
- молекулярный
коэффициент диффузии ионов в свободной
воде;
![]() - геометрический
фактор, определяемый через
- геометрический
фактор, определяемый через
![]() ,
где
,
где
![]() и
- сжимаемость и извилистость пор,
соответственно;
и
- сжимаемость и извилистость пор,
соответственно;
![]() - коэффициент
распределения, т.е. используем приближение
линейной изотермы адсорбции;
- коэффициент
распределения, т.е. используем приближение
линейной изотермы адсорбции;
![]() и
и
![]() - пористость и плотность «скелета»
породы, причем
- пористость и плотность «скелета»
породы, причем
![]() ,
где
,
где
![]() - насыпная плотность породы в сухом
состоянии;
- насыпная плотность породы в сухом
состоянии;
![]() - коэффициент
задержки в матрице породы.
- коэффициент
задержки в матрице породы.
Отдельным образом опишем граничное условие на левой границе для перечисленных выше моделей высвобождения активности.
Модель №1
|
(23.4) |
Модель №2
|
(23.5) |
Модель №3
|
(23.6) |
Модель №4
|
(23.7) |
где
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() и
и
![]() - доли «быстрой» и «медленной» компонент
выщелачивания;
- доли «быстрой» и «медленной» компонент
выщелачивания;
![]() и
и
![]() - коэффициенты скорости выщелачивания
соответствующих компонент;
- коэффициенты скорости выщелачивания
соответствующих компонент;
![]() - начальная
активность радионуклида в отвержденной
форме.
- начальная
активность радионуклида в отвержденной
форме.
Таким образом, предстоит в рамках диффузионного переноса пошагово решить следующие четыре задачи, каждая из которых описывается несколькими уравнениями:
- первая - (23.2)-(23.3) и (23.4);
- вторая - (23.2)-(23.3) и (23.5);
- тертья - (23.2)-(23.3) и (23.6) и
- четвертая - (23.2)-(23.3) и (23.7).
Оказывается, что несколько шагов при решении указанных задач совпадают. Проделаем последовательно общие шаги.
Первый шаг.
Вводим новую функцию
![]() .
Тогда уравнение (23.2) может быть переписано
в виде (авторы рекомендуют читателю
проверить «руками» такое преобразование)
.
Тогда уравнение (23.2) может быть переписано
в виде (авторы рекомендуют читателю
проверить «руками» такое преобразование)
|
(23.8) |
Второй шаг. К уравнению (23.8) применяем преобразование Лапласа
|
(23.9) |
С учетом основной теоремы операционного метода и начального нулевого распределения концентрации, выражение (23.9) в переменных изображения принимает вид
|
|
или
|
|
Третий шаг. Ищем решение уравнения (23.10). В общем виде решение этого уравнения имеет стандартный вид
|
|
Из граничного
условия на правой границе (![]() )
естественно записать
)
естественно записать
![]() .
Таким образом, вид решения уравнения
(23.10) довольно простой
.
Таким образом, вид решения уравнения
(23.10) довольно простой
|
|
Осталось определить
константу
![]() ,
для чего и будем использовать левое
граничное условие – при
,
для чего и будем использовать левое
граничное условие – при
![]() .
.
Естественно, что теперь необходимо работать с конкретным граничным условием. При этом необходимо помнить, что
|
|
Четвертый шаг для граничного условия (23.4). Применим к нему преобразование Лапласа.
|
|
С другой стороны, учитывая (23.11) и (23.12), имеем
|
|
Откуда легко получается выражение для коэффициента
|
|
Теперь уже есть возможность окончательно записать функцию (23.12)
|
|
Теперь, обратившись к таблицам обратного преобразования Лапласа, есть возможность записать искомую функцию в переменных оригинала
|
|
Четвертый шаг для граничного условия (23.5). Применим к нему преобразование Лапласа.
|
|
С другой стороны, учитывая (22.11) и (22.12), имеем
|
|
Откуда легко плучается выражения для коэффициента
|
|
Теперь уже есть возможность окончательно записать вид функции (23.12)
|
|
Обращаемся к таблицам обратного преобразования Лапласа и записываем искомую функцию в переменных оригинала
|
|
|
|
Четвертый шаг
для граничного условия (23.6).
Вычислим первую производную функции
(23.12)
![]() по пространственной координате
по пространственной координате
|
Теперь применим преобразование Лапласа к граничному условию (23.6), используя при этом соответствующие свойства преобразования
|
Откуда легко плучается выражения для коэффициента
|
Теперь уже есть возможность окончательно записать вид функции (23.12)
|
|
Здесь удобно ввести обозначения.
|
Теперь можно обратиться к таблицам обратного преобразования Лапласа (например, позиция 23.142 [5]) и записать искомую функцию в переменных оригинала
|
(23.18)
|
Четвертый шаг для граничного условия (23.7). Константу определим из граничного условия на поверхности источника
|
|
Тогда уравнение (23.11) примет вид
|
|
Здесь необходимо
записать уравнение баланса радиоактивности
![]() во вмещающем массиве, что возможно с
учетом используемого граничного условия
(23.7)
во вмещающем массиве, что возможно с
учетом используемого граничного условия
(23.7)
|
|
Подставляем в
уравнение (23.20) выражение для потока
двухкомпонентной модели выщелачивания
и снова воспользуемся преобразованием
Лапласа
![]() .
С учетом нулевого начального распределения
радиоактивности получим
.
С учетом нулевого начального распределения
радиоактивности получим
|
|
С учетом (23.12) возвращаемся к балансу радиоактивности во вмещающем массиве, но уже в переменных изображения и в интегральной форме
|
|
|
Интеграл (23.22) не является самым сложным
|
|
С учетом (23.21)
получаем выражение для
![]()
|
|
Здесь удобно ввести обозначения с тем, чтобы выражение (23.23) записать в необходимой для дальнейших шагов форме, в частности
|
|
После указанной подстановки выражение (23.23) принимает вид
|
|
Теперь можно обратиться к таблицам обратного преобразования Лапласа (например, позиция 23.142 [5]) и записать искомую функцию в терминах оригинала для двухкомпонентной модели выщелачивания
|
|
|
|
|
|
|
|
К огромному
сожалению, выражение (23.25) не может быть
непосредственно использовано для
вычислений, поскольку выражение
![]() .
Предварительно, требуется кропотливо
«поработать» над выражением (23.25) и
выделить из него имеено вещественную
часть. Но здесь будут использованы
другие методы, а не преобразование
Лапласа.
.
Предварительно, требуется кропотливо
«поработать» над выражением (23.25) и
выделить из него имеено вещественную
часть. Но здесь будут использованы
другие методы, а не преобразование
Лапласа.
Обобщим результаты решения диффузионной задачи. Таким образом, можно констатировать следующее:
- выражение (23.14) является решением диффузионной задачи (23.2)-(23.3) с граничным условием (23.4) – модель мгновенного растворения;
- выражение (23.18) - с граничным условием (23.5) – модель предела растворимости;
- выражение (23.21) – с граничным условием (23.6) – простейшая модель выщелачивания;
- выражение (23.25) – с граничным условием (23.7) – двухкомпонентная модель выщелачивания.
Модель адвекции-диффузии
Для моделирования переноса радиоактивности по трещине была выбрана известная модель D.Tang и его коллег [6], так называемая модель одиночной трещины (рис.23.2). Приведенная ниже система уравнений (23.26)- (23.29) записана при следующих предположениях по геометрии и гидравлическим свойствам физической системы (рис. 23.3):
- ширина трещины много меньше ее длины ;
- поперечная диффузия и дисперсия в пределах трещины гарантирует полное смешение потока поперек трещины. В пособии рассматривается и в миграционной подмодели программно реализован [1] вариант с нулевой дисперсией, что, как показали D. Tang и его коллеги, справедливо при скоростях движения воды по трещинам на уровне единиц метров в год;
- в матрице «работают» только диффузионные механизмы;
- перенос в трещине более быстрый, чем в матрице;
- некоторая часть радионуклидов диффундирует в микропоры матрицы породы вследствие различий концентрации на границе раздела трещина-матрица;
- гидрологические параметры постоянные;
- линейная изотерма адсорбции радионуклидов справедлива, как в матрице породы, так и на поверхности трещины.
трещина
|
|
|
|
матрица породы
|
|
|
|
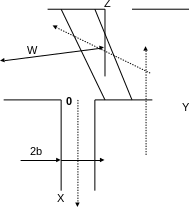
Рис. 23.2. Схематичное представление модели
где
![]() - концентрация радиоактивного вещества,
растворенного в воде трещины;
- концентрация радиоактивного вещества,
растворенного в воде трещины;
![]() - концентрация
радиоактивного вещества, растворенного
в воде порового пространства матрицы;
- концентрация
радиоактивного вещества, растворенного
в воде порового пространства матрицы;
![]() - пространственные
координаты;
- пространственные
координаты;
![]() - коэффициент
задержки в трещине, который определяется
следующим образом
- коэффициент
задержки в трещине, который определяется
следующим образом
![]() ;
;
![]() - коэффициент
поверхностной сорбции в трещине, имеющий
размерность длины и определяемый как
«масса растворенного вещества,
адсорбируемая на единице площади
поверхности и деленная на концентрацию
растворенного вещества»
- коэффициент
поверхностной сорбции в трещине, имеющий
размерность длины и определяемый как
«масса растворенного вещества,
адсорбируемая на единице площади
поверхности и деленная на концентрацию
растворенного вещества»
![]() ;
;
![]() - радиус мигрирующей
частицы;
- радиус мигрирующей
частицы;
- постоянное значение концентрации, задаваемое на входе в трещину. Относительно этой физической величины имеются определенные соображения, но, учитывая направленность пособия, здесь они не описываются.

Рис.23.3. Модель одиночной трещины
Решение системы уравнений (23.26)-(23.29) получается методом преобразования Лапласа. К уравнениям (23.26) и (23.29) применям преобразование Лапласа и основную теорему этого метода. Тогда с учетом начального распределения активности в трещине и матрице получим
|
|
|
|
Для дальнейших шагов последние два уравнения удобно записать в другой форме
|
|
|
|
Решение уравнения (23.30) ищем, как и ранее, в традиционном виде
|
|
Из граничного
условия на бесконечости (![]() )
имеем
,
а поскольку стенка трещины имеет
координату
)
имеем
,
а поскольку стенка трещины имеет
координату
![]() ,
то решение ищется в виде
,
то решение ищется в виде
|
|
Для упрощения
дальнейших преобразований введем
следующее обозначение
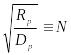 .
В этих обозначениях выражение (23.32)
немного упрощается. Кроме того, напомним,
что на стенке трещины справедливо
условие
.
В этих обозначениях выражение (23.32)
немного упрощается. Кроме того, напомним,
что на стенке трещины справедливо
условие
![]() .
Но тогда выражение (23.32) принимает вид
.
Но тогда выражение (23.32) принимает вид
|
|
Найдем производную
функции
![]() на стенке (
)
на стенке (
)
|
|
Теперь уравнение (23.31) можно переписать в виде
|
|
Через два новых
обозначения
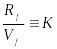 и
и
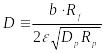 последнее выражение существенно
упрощается для выполнения последующих
действий
последнее выражение существенно
упрощается для выполнения последующих
действий
|
|
Решение дифференциального уравнения первого порядка (23.35) с учетом граничного условия (23.27) – постоянства концентрации на входе в трещину – запишется в виде
|
|
Решение для
концентрации в матрице породы в переменных
изображения легко получается из
комбинации уравнений (23.33) и (23.36). Если
снова для упрощения формул ввести
обозначение
![]() ,
то решение для
примет вид
,
то решение для
примет вид
|
|
Для выполнения
обратного преобразования Лапласа с
помощью табличных функций (например,
[5]) оказывается удобно перейти для
переменных изображения к следующему
обозначению
![]() .
Тогда уравнения (23.36) и (23.37), соответственно,
примут вид
.
Тогда уравнения (23.36) и (23.37), соответственно,
примут вид
|
|
|
|
Здесь на помощь приходит, первую очередь, основное функциональное соотношение обратного преобразования Лапласа
|
|
а во вторую очередь, позиция 23.124 [5]. Для заключительного шага удобны обозначения
|
Решение исходной
системы уравнений для функции
![]() ,
описывающей распределение концентрации
радиоактивности в трещине и справедливое
для условия
,
описывающей распределение концентрации
радиоактивности в трещине и справедливое
для условия
![]() ,
имеет вид:
,
имеет вид:
|
|
|
|
а
решение исходной системы уравнений для
функции
![]() ,
описывающей распределение концентрации
радиоактивности в матрице породы и
справедливое также для условия
,
имеет вид:
,
описывающей распределение концентрации
радиоактивности в матрице породы и
справедливое также для условия
,
имеет вид:
|
|
|
|
Таким образом, уравнения (23.40) и (23.41) с указанными выше обозначениями являются рещением исходной системы уравнений в приближении модели одиночной трещины с постояным значением концентрации на входе в трещину.

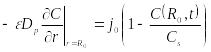 ,
,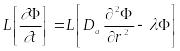 ,
, ,
, ,
(23.11)
,
(23.11)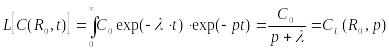 ,
, ,
,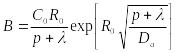 ,
,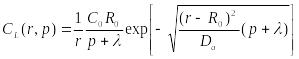 ,
(22.13)
,
(22.13)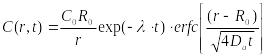 ,
(23.14)
,
(23.14)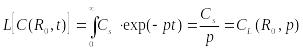 ,
, ,
,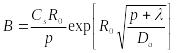 ,
,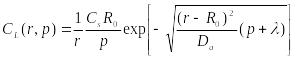 ,
(23.15)
,
(23.15)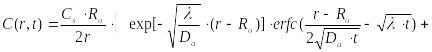
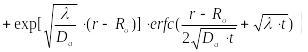 ,
(23.16)
,
(23.16)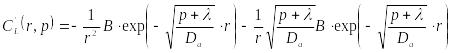
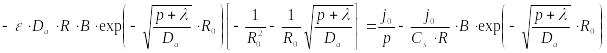
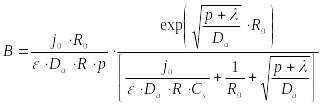
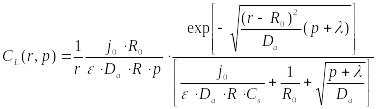 ,
(23.17)
,
(23.17)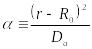 ,
,

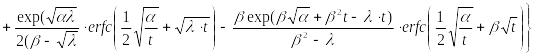
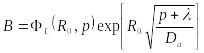 ,
, ,
(23.19)
,
(23.19)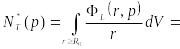 ,
(23.22)
,
(23.22)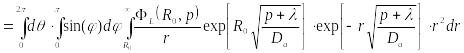 ,
,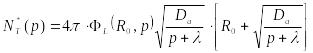 ,
, ,
(22.23)
,
(22.23)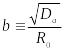 ,
,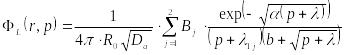 ,
(23.24)
,
(23.24)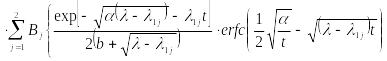
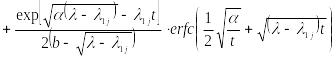
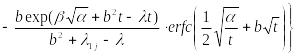 (23.25)
(23.25)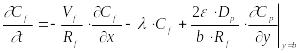 ,
(23.26)
,
(23.26)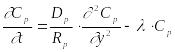 ,
(23.28)
,
(23.28) ,
,
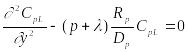 (23.30)
(23.30)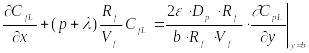 .
(23.31)
.
(23.31)
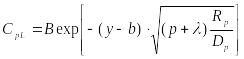 (23.32)
(23.32)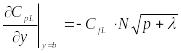 .
(23.34)
.
(23.34)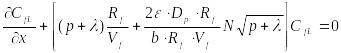 .
.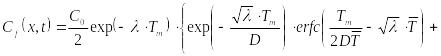
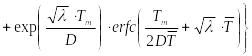 ,
(23.40)
,
(23.40)