21.3. Свертка функций
Формула
Дирихле.
Пусть
непрерывна
в треугольнике
:
(рис.
21.1).
Рис. 21.1
Преобразуя
двойной интеграл
двумя способами в двукратный и сравнивая
результаты, получим искомую формулу
Дирихле:
(21.3)
Свертка
функций. Пусть
и
— непрерывные, комплекснозначные
функции на
.
Сверткой
функций
и
называется функция, обозначаемая
＊
и
определяемая равенством
(
＊
)
.
Это будет непрерывная функция на . Очевидно,
＊
＊
при с помощью формулы Дирихле находим:
＊
;
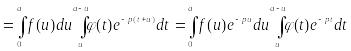следовательно, если записать внутренний интеграл
в
виде
-
,
получим
формулу
＊
(21.4)
Из
(21.4)
следует, что при
и
и действительном
＊
,
откуда видно, что если и оригиналы, то ＊ — тоже оригинал, причем показатель роста ＊ не более наибольшего из показателей роста и .
Свертка оригиналов.
Теорема.
При
свертывании оригиналов изображения
перемножаются, т.е. если
≒
и
≒
,
то
＊
≒
.
Доказательство.
Для простоты мы имеем в виду лишь
непрерывные на
оригиналы. Учитывая формулу (19.4),
достаточно показать, что
при
.
Пусть
≒
и
≒
,
тогда,
если Rе
больше показателей роста
и
,
то
,
что
при
,
что и требовалось доказать.
Пример.
Найти
свертку
и
,
где
,
.
Делая в интеграле подстановку
и
учитывая формулы
и
,
где
и
– гамма-функции, или эйлеровы интегралы
2-го рода, которые определяются для
положительных значений независимых
переменных
и
формулами:
и
,
＊
и, в
частности, при целых неотрицательных
,
и
Следовательно, искомая свертка имеет вид
＊
.
Формула
Дюамеля. Пусть
-
непрерывный на
оригинал,
-
непрерывно дифференцируемая на
функция такая, что
есть
оригинал. Из
≒
и
≒
следует:
≒
Из правила дифференцирования интегралов, зависящих от параметра, следует, что левая часть непрерывно дифференцируема на , причем
Отсюда в силу свойства 4 (см. 21.2) [дифференцирование оригинала ] получаем искомую формулу Дюамеля
≒
(21.5)
21.4. Оригиналы с рациональными изображениями
Изображения некоторых элементарных функций.
1.
Изображения
степенных и показательных функций.
При
степенная функция
является оригиналом с нулевым показателем
поста, причем
,
что
при положительных значениях
равно
(после замены
на t)
(21.6)
Необходимо
отметить, что в силу теоремы
единственности,
которая гласит: если в области
даны две аналитические функции,
совпадающие на множестве точек, имеющем
хотя бы одну предельную точку, лежащую
в области
,
то эти две функции тождественно равны,
изображение
и правой часть равенства (21.6)
аналитичны в полуплоскости Rе
,
следовательно, совпадая в положительных
точках, они совпадают на всей полуплоскости
Rе
(заметим, что степенные функции
комплексного
переменного
многозначны
при нецелых
,
но, рассматривая их на полуплоскости
Rе
,
мы всякий раз имеем в виду те их ветви,
которые происходят от ветвей
,
совпадающих
для положительных
с
).
Итак,
≒
(
) (21.7)
Так,
при
≒
(21.8)
и, в
частности, при
1≒
(21.9)
Из (21.8) по правилу смещения изображений (1.2 свойство 9 - ≒ ) находим при любом целом неотрицательном и любом комплексном
≒
(21.10)
и, в частности, при
≒
(21.11)
2. Изображения тригонометрических и гиперболических функций. В силу (21.10) имеем:
≒
(21.12)
≒
(21.13)
≒
(21.14)
≒
(21.15)
Из (21.12) и (21.13) по правилу подобия (1.2, свойство 3 - ≒ ) находим:
≒
(21.16)
≒
(21.17)
откуда
по правилу смещения изображений (1. 2,
свойство 9 -
≒
)
≒
(21.18)
≒
(21.19)
Условие рациональности изображения.
3. Изображения линейной комбинации функций вида .
Изображения линейной комбинации функций вида ( - целое неотрицательное, - комплексное) всегда являются рациональными, т.е. всякая правильная рациональная дробь является изображением некоторого оригинала. Поэтому, с помощью преобразования Лапласа можно устанавить взаимно однозначное соответствие между всеми функциями, являющимися линейными комбинациями выражений tmet, и всеми правильными рациональными дробями.
Необходимо отметить, что класс функций, являющихся линейными комбинациями выражений вида , обладает следующими свойствами:
- операции линейного комбинирования,
- умножения на аргумент,
- умножения на показательную функцию,
- линейного преобразования аргумента,
- дифференцирования и интегрирования,
примененные к функциям этого класса, приводят снова к функциям этого класса.