
- •Часть 2. Дифференциальные уравнения в частных производных первого порядка Лекция 11. Уравнения в частных производных первого порядка
- •11.1. Линейные и квазилинейные уравнения
- •11.2. Уравнения с переменными коэффициентами. Характеристики
- •11.3. Решение задачи Коши
- •12.2. Уравнение колебаний стержня
- •12.3. Уравнение теплопроводности и диффузии
- •12.4. Уравнения гидродинамики и звуковых волн
- •Лекция 13. Классификация уравнений в частных производных 2-го порядка, приведение их к каноническому виду и нахождение общего решения
- •Задания для самостоятельной работы
- •Лекция 14. Начальные и граничные условия
- •14.1. Начальные условия
- •14.2. Краевые задачи
- •Лекция 15. Решение задачи коши для волнового уравнения
- •15.1. Решение задачи Коши методом Даламбера
- •15.2. Решение задачи Коши для волнового уравнения методом Тейлора
- •Задания для самостоятельной работы
- •Лекция 16. Решение граничных задач волнового уравнения
- •16.1. Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны
- •16.2. Метод Фурье (метод разделения переменных) для уравнения вынужденных колебаний струны
- •Задания для самостоятельной работы
- •Лекция 16 (продолжение). Задача о напряженном состоянии элемента вооружения долота режущего действия
- •Лекция 17. Уравнения теплопроводности (диффузии) и методы их решений
- •17.1. Методы решения задачи Коши
- •Задания для самостоятельной работы
- •17.2. Методы решения граничных задач
- •Лекция 17 (продолжение). Расчет глубины промерзания связанных горных пород
- •Лекция 18. Стационарные уравнения. Уравнение лапласа и методы его решения
- •18.1.Задачи, приводящие к уравнениям эллиптического типа
- •18.2. Решения краевых задач для уравнения Лапласа в круге
- •Задания для самостоятельной работы
- •Лекция 19. Уравнение неразрывности и уравнения эйлера
- •19.1. Гипотеза сплошности
- •19.2. Установившееся и неустановившееся движения.
- •19.3. Уравнения гидродинамики и звуковых волн
- •19.4. Закономерности распространения плоских упругих волн
- •Лекция 20. Закономерности преломления и отражения плоских упругих волн на плоскости контакта твердых тел
- •Часть 4. Преобразование лапласа и его применение при решении дифференциальных уравнений Лекция 21. Преобразование лапласа
- •21.1. Преобразование Лапласа
- •21.2. Основные свойства преобразования Лапласа
- •21.3. Свертка функций
- •21.4. Оригиналы с рациональными изображениями
- •21.5. Нахождение оригинала по заданному изображению (когда оно рационально)
- •21.6. Оригиналы с изображениями, регулярными в бесконечности
- •Лекция 22. Практическое применение преобразования лапласа
- •22.1. Приложения к решению линейных дифференциальных уравнений с постоянными коэффициентами
- •22.2. Использование преобразования Лапласа при решении уравнений в частных производных
- •Лекция 23. Миграционная подмодель радиогеоэкологической модели подземного регионального хранилища радиоактивных отходов и ядерных материалов
- •Вопросы к экзамену по дисциплине: «Дифференциальные уравнения в горном деле»
Лекция 18. Стационарные уравнения. Уравнение лапласа и методы его решения
18.1.Задачи, приводящие к уравнениям эллиптического типа
Рассмотрим движение
несжимаемой жидкости. Пусть некий
произвольный фиксированный объем V
жидкости, ограниченный поверхностью
S,
и массой т
движется со скоростью
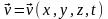 .
Масса т
связана с плотностью
.
Масса т
связана с плотностью
 соотношением
соотношением
 . (18.1)
. (18.1)
Эта масса может изменяться за счет потока жидкости через поверхность S, причем
 , (18.2)
, (18.2)
где
 -
внешняя нормаль к S.
Тогда из уравнений (18.1) и (18.2) получаем
-
внешняя нормаль к S.
Тогда из уравнений (18.1) и (18.2) получаем
 . (18.3)
. (18.3)
Преобразуя
поверхностный интеграл, находящийся в
правой части выражения (18.3) по формуле
Остроградского ( ),
запишем формулу (18.3) в виде
),
запишем формулу (18.3) в виде
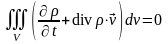 .
.
Отсюда в силу произвольности выделенного объема V следует
 .
.
Это уравнение
называют уравнением
неразрывности
сплошной среды. Для несжимаемой жидкости
плотность
 ,
и из уравнения неразрывности следует,
что
,
и из уравнения неразрывности следует,
что
 . (18.4)
. (18.4)
Рассмотрим
установившееся течение несжимаемой
жидкости, для которого
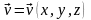 .
Если это течение безвихревое, то
существует потенциал скоростей
.
Если это течение безвихревое, то
существует потенциал скоростей
 ,
такой, что
,
такой, что
 . (18.5)
. (18.5)
или
 ,
или
,
или
 , (18.6)
, (18.6)
т.е. потенциал скоростей удовлетворяет уравнению (18.6), которое является уравнением эллиптического типа и называется уравнением Лапласа.
Запишем теорему
Гаусса для электростатического поля
напряженностью
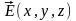 в вакууме
в вакууме
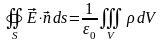 . (18.7)
. (18.7)
где
 -
электрическая постоянная в системе Си;
-
электрическая постоянная в системе Си;
 - объемная плотность электрических
зарядов; V
– некоторый объем пространства,
ограниченный замкнутой поверхностью
S.
С помощью теоремы Остроградского
соотношение (18.7) можно преобразовать к
дифференциальной форме
- объемная плотность электрических
зарядов; V
– некоторый объем пространства,
ограниченный замкнутой поверхностью
S.
С помощью теоремы Остроградского
соотношение (18.7) можно преобразовать к
дифференциальной форме
 . (18.8)
. (18.8)
Поскольку напряженность поля связана с потенциалом этого поля соотношением
 ,
,
то из (18.8) получим уравнение для потенциала электростатического поля
 , (18.9)
, (18.9)
которое будет являться уравнением эллиптического типа и называться уравнением Пуассона.
Как и уравнение Лапласа, так и уравнение Пуассона являются стационарными уравнениями, т.к. искомая функция не зависит от времени.
Уравнение Лапласа можно записать не только в системе декартовых координат (18.6), но и цилиндрической системе
 (18.10)
(18.10)
и сферической системе координат
 . (18.11)
. (18.11)
С уравнением
Лапласа связано понятие гармонической
функции. Функцию называют гармонической
в
некоторой области D,
если в этой области она непрерывна
вместе со своими частными производными
до второго порядка включительно и
удовлетворяет уравнению Лапласа. Так,
если функция
 зависит только от расстояния
зависит только от расстояния
 точки
точки
 до начала координат, то уравнение Лапласа
будет иметь вид
до начала координат, то уравнение Лапласа
будет иметь вид
 ,
,
если С1
= -1, а С2
= 0, то функция
 будет гармонической функцией везде в
области D
за исключением точки
и будет называться фундаментальным
решением уравнения Лапласа в пространстве.
будет гармонической функцией везде в
области D
за исключением точки
и будет называться фундаментальным
решением уравнения Лапласа в пространстве.
Если функция
зависит только от расстояния
 точки
точки
 до начала координат, то уравнение Лапласа
будет иметь вид
до начала координат, то уравнение Лапласа
будет иметь вид
 ,
,
и если С1
= -1, а С2
= 0, то функция
 будет гармонической функцией везде в
области D
за исключением точки
и будет называться фундаментальным
решением уравнения Лапласа на плоскости.
будет гармонической функцией везде в
области D
за исключением точки
и будет называться фундаментальным
решением уравнения Лапласа на плоскости.
18.2. Решения краевых задач для уравнения Лапласа в круге
Уравнением Лапласа описываются различные физические процессы и в каждой задаче искомое решение должно удовлетворять уравнению в некоторой области D, а также некоторому дополнительному условию на границе S этой области D.
В зависимости от вида граничного условия различают следующие основные виды граничных задач:
1) найти решение
уравнения Лапласа, удовлетворяющее
граничным условиям первого рода:
 - первая краевая задача или задача
Дирихле;
- первая краевая задача или задача
Дирихле;
2) найти решение
уравнения Лапласа, удовлетворяющее
граничным условиям второго рода:
 - вторая краевая задача или задача
Неймана;
- вторая краевая задача или задача
Неймана;
3) найти решение
уравнения Лапласа, удовлетворяющее
граничным условиям третьего рода:
 - третья краевая задача,
- третья краевая задача,
где
 - определенные на поверхности S
функции; Р
– точка поверхности S;
- внешняя нормаль к S;
- определенные на поверхности S
функции; Р
– точка поверхности S;
- внешняя нормаль к S;
 .
.
Краевые задачи могут быть внутренними или внешними. Они различаются в зависимости от того, в какой области внутренней или внешней относительно поверхности S ищется решение.
Внутренняя задача Дирихле формулируется следующим образом: Найти непрерывную в замкнутой области функцию и(М), которая удовлетворяла бы в области D уравнению Лапласа и принимала бы на поверхности S заданные значения F(P). Математически это можно записать следующим образом:

Внутренняя задача Неймана формулируется так: найти внутри области D решение и(М) уравнения Лапласа

непрерывное в замкнутой области и удовлетворяющее на поверхности S условию
Рассмотрим теперь
краевые задачи для уравнения Лапласа
внутри круга и вне его. Пусть существует
область, представляющая собой круг
радиуса R.
Запишем двухмерное уравнение Лапласа
в полярных координатах, полагая, что
 ,
а
,
а
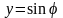
 или
или
 .
(18.12)
.
(18.12)
Для нахождения частных решений уравнения (18.12) используем метод Фурье и представим эти решения в виде
 (18.13)
(18.13)
После подстановки решения (18,13), первой и второй производной от этой функции по r, а также второй производной от нее по φ в исходное уравнение (18.12), получим
 .
.
Разделим в этом уравнении переменные
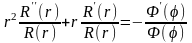 (18.14)
(18.14)
Это равенство выполняется тогда и только тогда, если обе его части равны одной и той же постоянной, например, λ

Тогда
для каждой функции
 и
и
 получим два уравнения
получим два уравнения
 , (18.15)
, (18.15)
 . (18.16)
. (18.16)
Рассмотрим сначала
уравнение (18.15) для функции
.
Ясно, что при изменении угла φ
на величину 2π однозначная функция
 должна вернуться к исходному значению,
т.е.
должна вернуться к исходному значению,
т.е.
 .
Отсюда
.
Отсюда
 .
Значит,
.
Значит,
 ,
т.е. функция
является периодической функцией с
периодом 2π. Уравнение (18.15) является
линейным однородным уравнением второго
порядка и поэтому его решение будем
искать в виде
,
т.е. функция
является периодической функцией с
периодом 2π. Уравнение (18.15) является
линейным однородным уравнением второго
порядка и поэтому его решение будем
искать в виде
 ,
,
После подстановки которого в уравнение (18.15) получим характеристическое уравнение
 ,
,
Корни характеристического
уравнения являются исключительно
мнимыми, поэтому общее решение уравнения
(18.15) при
 будет
иметь вид,
будет
иметь вид,
 . (18.17)
. (18.17)
и
в силу периодичности функции
должно быть выполнено равенство
 ,
где n
≥ 0 – целое число.
,
где n
≥ 0 – целое число.
В самом деле, из равенства
 ,
,
Введем обозначения
 ,
,
тогда можно записать
 ,
,
т.е.
 , (18.18)
, (18.18)
где n ≥ 0 – целое число.
Следовательно, частные решения уравнения (18.15) при различных значениях n можно записать в виде
 (18.19)
(18.19)
Исходя из (18.18) следует, что уравнение (18.16) можно записать в виде
 (18.20)
(18.20)
Уравнение (18.20) в
случае, когда
 представляет собой уравнение Эйлера с
переменными коэффициентами, которое
можно привести к уравнению с постоянными
коэффициентами используя замену
переменной по правилу
представляет собой уравнение Эйлера с
переменными коэффициентами, которое
можно привести к уравнению с постоянными
коэффициентами используя замену
переменной по правилу
 .
Вычислим производные уравнения (18.20) в
новых переменных
.
Вычислим производные уравнения (18.20) в
новых переменных
 .
.
Следовательно, подставив эти производные в уравнение (18.19) получим обыкновенное линейное и однородное дифференциальное уравнение с постоянными коэффициентами
 . (18.21)
. (18.21)
Решение этого уравнения будем искать в виде
 ,
,
Вычислим от этой функции производные и подставим в уравнение (18.21)
 ,
,
следовательно общее решение уравнения (18.21) имеет вид

и возвращаясь к переменной r, получим
 . (18.22)
. (18.22)
Если в уравнении
(18.20)
 ,
то это уравнение принимает вид
,
то это уравнение принимает вид
 (18.23)
(18.23)
Это уравнение
также является уравнением Эйлера,
поэтому, производя замену
 ,
приходим к уравнению
,
приходим к уравнению
 ,
,
решение которого будет иметь вид
 ,
,
и возвращаясь к переменной r, получим
 . (18.24)
. (18.24)
решение уравнения (18.20) при , а при любых значениях n частные решения уравнения (18.20) запишем в виде
 . (18.25)
. (18.25)
Подставляя (18.19) и (18.25) в решение (18.13) получим набор частных решений
 ,
,
используя принцип суперпозиции, а также вследствие линейности и однородности уравнения Лапласа можно утверждать, что сумма частных решений также будет его решением, следовательно, общее решение уравнения Лапласа будет иметь вид
 (18.26)
(18.26)
Пользуясь этой формулой и задавая граничные условия первого, второго и третьего рода можно решать как внутренние, таки внешние граничные задачи – Дирихле, Неймана и смешанную задачу.
Рассмотрим внутреннюю задачу Дирихле для уравнения Лапласа в круге радиуса R

Для
решения этой задачи используем формулу
(18.26), учитывая при этом, что функция
 должна быть ограничена, поэтом мы должны
принять, что все коэффициенты
должна быть ограничена, поэтом мы должны
принять, что все коэффициенты
 ,
поскольку в противном случае функция
имела бы разрыв в точке r
= 0 и не была бы гармонической в круге.
Исходя из этого, и полагая, что все
коэффициенты
,
поскольку в противном случае функция
имела бы разрыв в точке r
= 0 и не была бы гармонической в круге.
Исходя из этого, и полагая, что все
коэффициенты
 ,
а также в формуле (18.26) выделяя члены при
n
= 0,
,
а также в формуле (18.26) выделяя члены при
n
= 0,

получим решение уравнения Лапласа
 (18.27)
(18.27)
Удовлетворим в этом решении поставленным граничным условиям

Разложим функцию f(φ) в ряд Фурье на интервале от 0 до 2π
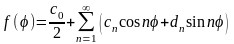 ,
,
следовательно, можно записать
 .
.
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства
,
найдем значения искомых коэффициентов An и Bn

Подставляя найденные коэффициенты в решение (18.27), получим окончательное решение внутренней задачи Дирихле для уравнения Лапласа в круге
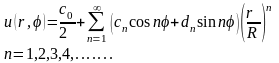 (18.28)
(18.28)
где cn и dn коэффициенты, заданные поставленными граничными условиями.
Решение задачи Дирихле также можно получить и используя формулу Пуассона
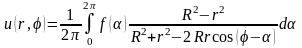 , (18.29)
, (18.29)
которая
при непрерывной функции
 дает классическое решение задачи Дирихле
в круге.
дает классическое решение задачи Дирихле
в круге.
Рассмотрим внешнюю задачу Дирихле для уравнения Лапласа в круге радиуса R
Для
решения этой задачи используем формулу
(18.26), учитывая при этом, что функция
должна быть ограничена на бесконечности
и неограниченна при r
→ 0, поэтом мы должны принять, что все
коэффициенты
 .
Исходя из этого, и полагая, что все
коэффициенты
.
Исходя из этого, и полагая, что все
коэффициенты
 ,
получим решение уравнения Лапласа
,
получим решение уравнения Лапласа
 (18.30)
(18.30)
Удовлетворим в этом решении поставленным граничным условиям
 ,
и разложим функцию f(φ)
в ряд Фурье на интервале от 0 до 2π
,
и разложим функцию f(φ)
в ряд Фурье на интервале от 0 до 2π
.
Следовательно, можно записать
 .
.
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства
,
найдем значения искомых коэффициентов An и Bn

Подставляя найденные коэффициенты в решение (18.30), получим окончательное решение внутренней задачи Дирихле для уравнения Лапласа в круге
 ,
(18.31)
,
(18.31)
где cn и dn коэффициенты, заданные поставленными граничными условиями.
Рассмотрим внутреннюю задачу Неймана:
 (18.32)
(18.32)
Для решения этой задачи вычислим производную от решения (18.27)
 . (18.33)
. (18.33)
И запишем граничные условия
 и разложим функцию
f(φ)
в ряд Фурье на интервале от 0 до 2π
и разложим функцию
f(φ)
в ряд Фурье на интервале от 0 до 2π
 .
.
Следовательно, можно записать
 .
.
Теперь, приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства, найдем значения искомых коэффициентов An и Bn

Подставляя найденные коэффициенты в решение (18.33), получим окончательное решение внутренней задачи Неймана для уравнения Лапласа в круге
 ,
(18.31)
,
(18.31)
где С – произвольная постоянная.
Необходимо отметить, что решение задачи Неймана существует только при условии
 (18.32)
(18.32)
и определяется с точностью до произвольной постоянной.
Смешанная граничная задача для уравнения Лапласа в круге радиуса R решается аналогично задачам рассмотренным выше.
Пример П18.1. Найти решение уравнения Лапласа для внутренней части круга радиуса R, удовлетворяющее краевому условию
 .
(П18.1.1)
.
(П18.1.1)
▲ Здесь задана
задача Дирихле, где правая часть
граничного условия (П18.1.1)
 .
Решение ищется в круге
.
Решение ищется в круге
 ,
значит выписывать решение будем по
(18.28). Найдем в этой формуле коэффициенты
,
значит выписывать решение будем по
(18.28). Найдем в этой формуле коэффициенты

Для этого подставим
само решение (18.28) в левую часть граничного
условия (П18.1.1)
при
 ,
а правую часть, т.е. функцию
,
а правую часть, т.е. функцию
 разложим в ряд Фурье по синусам и
косинусам
разложим в ряд Фурье по синусам и
косинусам
 .
(П18.1.2)
.
(П18.1.2)
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами и при свободном члене в левой и правой частях полученного равенства (П18.1.2)
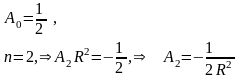
 (при
(при
 ),
т.к. справа нет слагаемых с
),
т.к. справа нет слагаемых с
 ,
,
а
также все остальные
 (кроме
(кроме
 ).
Подставим ненулевые
).
Подставим ненулевые
 в решение (18.28) и получим ответ, т.е. найдем
функцию
в решение (18.28) и получим ответ, т.е. найдем
функцию
 ▲
▲
Пример П18.2. Найти решение уравнения Лапласа внутри круга радиуса R , удовлетворяющее на границе условию Неймана
 (П18.2.1)
(П18.2.1)
▲ Здесь задана
задача Неймана, где правая часть
граничного условия (П18.2.1)
 (уже разложена в ряд Фурье), которую
можно представить в виде двух функций
(уже разложена в ряд Фурье), которую
можно представить в виде двух функций

и для каждой из них найдем решение. Прежде чем решать поставленную задачу проверим выполнение условия (18.32)
 ,
,
так как условие (18.32) выполнено, то для решения поставленной задачи воспользуемся, описанном выше алгоритмом (III.)
Вычислим производную от решения (18.27)
.
и
запишем граничные условия сначала для
функции

 (П18.2.2)
(П18.2.2)
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (П18.2.2):

а все остальные и . Следовательно, решение, соответствующее функции имеет вид
 .
.
Затем
запишем граничные условия сначала для
функции

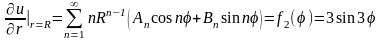 (П18.2.3)
(П18.2.3)
Теперь сравним коэффициенты при синусах и косинусах с одинаковыми аргументами в левой и правой частях полученного равенства (П18.2.3):

а все остальные .
Следовательно, решение, соответствующее функции имеет вид
 .
.
Таким образом, решение исходной задачи будет определяться формулой
 ▲
▲
