1.Предмет теории вероятности. Роль т.в. в соц-экономических исследованиях. Испытанием называютсся всякие действия направленные на достижение определённой цели. Результат испытания- событие. Все события делятся на: достоверные, невозможные и случайные. Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, хотя, как было уже сказано, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений герба, если монета будет брошена достаточно большое число раз. При этом 'предполагается, конечно, что монету бросают в одних и тех же условиях. Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей- служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей. В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу. Методы, основанные на теории вероятностей(статистичекие методы, статистика) находят применение при исследовании социально-экономических явлений и процессов: уровня жизни населения и динамики его, покупательского спроса, уровня интенсификации производства, оплаты труда, производства и качества продукции и т.д.

2.Виды случайных событий. Наблюдаемые нами события можно подразделить на следующие три вида: Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S .  Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S. Случайным событием(возможным событием или просто событием), называется любой факт, который в результате испытания может произойти или не произойти. Испытание(опыт, эксперимент) – выполнение определенного комплекса условий, в которых наблюдается то или иное явление , фиксируется тот или иной результат. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Например, брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.К примеру, стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.События называют равновозможными, если у них имеются одинаковые шансы появиться. Противоположные события- несовместны и при испытании одно из них обязательно произойдёт.

3.Пространство элементарных событий — множество Ω всех различных исходов случайного эксперимента. Элемент этого множества называется элементарным событием (исходом). Пространство элементарных событий называется дискретным, если число его элементов конечно (счётно). Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий Ω вместе с алгеброй событий и вероятностью образует тройку , которая называется вероятностным пространством. В теории вероятностей элементарные события (события-атомы) — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается Ω. Всякое подмножество множества Ω элементарных событий называется случайным событием. Говорят, что в результате эксперимента произошло случайное событие , если (элементарный) исход эксперимента является элементом A. В определении вероятностного пространства на множестве случайных событий вводится сигма-аддитивная конечная мера, называемая вероятностью. Элементарные события могут иметь вероятности, которые строго положительны, нули, неопределенны, или любая комбинация из этих вариантов. Например, любое дискретное вероятностное распределение определяется вероятностями того, что может быть названо элементарными событиями. Напротив, все элементарные события имеют вероятность нуль для непрерывного распределения. Смешанные распределения, не будучи ни непрерывными, ни дискретными, могут содержать атомы, которые могут мыслиться как элементарные события с ненулевой вероятностью. Элементарное событие — это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это всё ещё множество, но не сам элемент. Однако элементарные события обычно записываются как элементы, а не как множества с целью упрощения, когда это не может вызвать недоразумения. Примеры пространств исходов эксперимента, Ω, и элементарных событий:1)Если объекты счётны, а пространство исходов Ω = {0,1,2,3,...} (натуральные числа), то элементарные события — это любые множества {k}, где . 2)Если монета бросается дважды, Ω = {OO,OP,PO,PP}, O для орла, а P для решки, то элементарные события: {OO}, {OP}, {PO} и {PP}.

4.Классическая вероятность и ее свойства. Вероятность события – количественная мера возможности появления случайного события (Число, в котором измеряются шансы появиться случайному событию). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу(количественное опр-е). Итак, вероятность события А определяется формулой: Р (A) = m / n, где m - число элементарных исходов, благоприятствующих A; n - число всех возможных элементарных исходов испытания. Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Из определения вероятности вытекают следующие ее свойства: С в о й с т в о 1. Вероятность достоверного события равна единице. Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно, Р (A) = m / n = n / n = 1(т.е. Р(Ω)=1). С в о й с т в о 2. Вероятность невозможного события равна нулю.Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно, Р (А) = m / n = 0 / n = 0. С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей, т.е. 0 <= Р (A) <= 1.

5. Относительная частота. Статистическая вероятность. Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой : W (А) = m / n, где m - число появлений события, n - общее число испытаний. Статистическая вероятность - относительная частота, с которой событие появляется внутри класса событий. Статистической вероятностью события А называется относительная частота (частность) появления этого события в n произведенных испытаниях, т.е. P с волной (A) = w (A) = m/n, где P с волной (A) – статистическая вероятность события А; w (A) – относительная частота (частность) события А; m – число испытаний, в которых появилось событие А; n – общее число испытаний. В отличие от «математической» вероятности Р(А), рассматриваемой в классическом определении, статистическая вероятность P с волной (A) является характеристикой опытной, экспериментальной. Если Р(А) есть доля случаев, благоприятствующих событию А, к-ая определяется непосредственно, без каких-либо испытаний, то P с волной (A) есть доля тех фактически произведенных испытаний, в которых событие А появилось. Статистическое определение вероятности применимо к событиям, обладающим определенные св-ва:1) Рассматриваемые события должны быть исходами только тех испытаний, к-ые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий. 2)События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в различных сериях испытаний относительная частота события изменяется незначительно, колеблясь около постоянного числа. Оказалось, что этим постоянным числом является вероятность события. 3)Число испытаний, в результате к-ых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вероятность события Р(А) приблизительно равной ее относительной частоте. Теория вероятности изучает лишь такие события, в отношении к-ых имеет смысл не только утверждение об их случайности, но и возможна объективная оценка относительной частоты их появления.

6.Сумма событий. Теорема сложения вероятностей для несовместных событий. Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. В частности, если два события А и B — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С. Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В). Док-во: Введем обозначения: n — общее число возможных элементарных исходов испытания; m₁ — число исходов, благоприятствующих событию A; m₂— число исходов, благоприятствующих событию В. Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Следовательно, Р (A + В) = (m₁ + m₂) / n = m₁ / n + m₂ / n. Приняв во внимание, что m₁ / n = Р (А) и m₂ / n = Р (В), окончательно получим, Р (А + В) = Р (А) + Р (В). С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (A₁ + A₂ + ... + A_n) = Р (A₁) + Р (A₂) + ... + Р (A_n).

7.Условная вероятность.Теорема умножения вероятностей. Назовем условной вероятностью р(В/А) события В вероятность события В при условии, что событие А произошло. Замечание. Понятие условной вероятности используется в основном в случаях, когда осуществление события А изменяет вероятность события В. Примеры: 1)      пусть событие А – извлечение из колоды в 32 карты туза, а событие В – то, что и вторая вынутая из колоды карта окажется тузом. Тогда, если после первого раза карта была возвращена в колоду, то вероятность вынуть вторично туз не меняется:   Если же первая карта в колоду не возвращается, то осуществление события А приводит к тому, что в колоде осталась 31 карта, из которых только 3 туза. Поэтому  . Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:  р (АВ) = р (А) · р (В/А).  Доказательство: Пусть т_А – число исходов, благоприятных событию А, т_В – число исходов, благопри-ятных событию В, а т_АВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ).Тогда для вычисления р(В/А) множеством возможных исходов нужно считать т_А (так как А произошло), а множеством благоприятных исходов – те, при которых произошли и А, и В ( т_АВ ). Следовательно, ч. и т.д.

8. Зависимые и независимые события. Теорема умножения вероятностей для независимых событий. Два события называют зависимыми, если вероятность появления одного из них зависит от наступления или не наступления другого события. Событие В называют независимым от события А, если появления события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности: Pa(B)=P(B); Pb(A)=P(A). Два события называют независимыми, если вероятность их совмещений равна произведению вероятностей этих событий; иначе события "зависимые". "Несколько событий называются независимыми", если каждые два из них независимы. Например события А,В,С попарно независимы, если независимы события А и В, А и С, В и С. "Теорема умножения для независимых событий" имеет вид P(AB)=P(A)*P(B), т.е. вероятность появления двух независимых событий равна произведению вероятностей этих событий.

9.Теорема сложения вероятностей для совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B)=P(A)+P(B)-P(AB) (1) . Доказательство: Поскольку события А и В, по условию, совместны, то событие А+В наступит, если наступит одно из следующих трех совместных событий:  B, A  или AB. По теореме сложения вероятностей несовместных событий: P(A+B)=P( B)+P(A )+P(AB) (2). Событие А произойдет, если наступит одно из двух несовместных событий: A или AB. По теореме сложения вероятностей несовместных событий имеем: P(A)=P(A )+P(AB), Отсюда P(A )=P(A)-P(AB) , Аналогично имеем P(B)=P( B)+P(AB) , Отсюда P( B)=P(B)-P(AB), Подставив все в (2), окончательно получим P(A+B)=P(A)+P(B)-P(AB). Ч.и т.д.

10. Формула полной вероятности и формула Байеса Если событие А может произойти только при выполнении одного из событий  , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле: Эта формула называется формулой полной вероятности. Вновь рассмотрим полную группу несовместных событий  , вероятности появления которых  . Событие А может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Тогда по формуле полной вероятности: Если событие А произошло, то это может изменить вероятности гипотез  . По теореме умножения вероятностей ,откуда . Аналогично, для остальных гипотез

. Полученная формула называется формулой Байеса. Вероятности гипотез   называются апостериорными вероятностями, тогда как   -априорными вероятностями. Значение формулы Байеса состоит в том, что при наступлении события F,т.е. по мере получения новой инф-и, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе т.п.

11.Вероя́тностное простра́нство — понятие, введённое А. Н. Колмогоровым в 30-х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей как строгой математической дисциплины. Вероятностное пространство — это тройка , где :1) — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками; 2) — сигма-алгебра подмножеств , называемых (случайными) событиями; 3) — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что . [Замечания: 1.Элементарные события (элементы ), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. 2.Каждое случайное событие (элемент ) — это подмножество . Говорят, что в результате эксперимента произошло случайное событие , если (элементарный) исход эксперимента является элементом A. Требование, что является сигма-алгеброй подмножеств , позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.] Простым и часто используемым примером вероятностного пространства является конечное пространство. Пусть — конечное множество, содержащее элементов. В качестве сигма-алгебры удобно взять семейство всех подмножеств . Его часто символически обозначают . Число различных случайных событий, как раз равно . Вероятность, вообще можно определять произвольно. Часто, однако, нет причин считать, что один элементарный исход чем-либо предпочтительнее другого. Тогда естественным способом ввести вероятность является: , где , и - число элементарных исходов, принадлежащих . В частности, вероятность любого элементарного события:

12.Дискретные вероятностные пространства

Если множество элементарных исходов   конечно или счетно:  , то соответствующее вероятностное пространство называется дискретным. В случае дискретных вероятностных пространств событиями обычно считают все возможные подмножества  . В этом случае для задания вероятности необходимо и достаточно приписать каждому элементарному исходу   число   так, чтобы их сумма была равна 1. Тогда вероятность любого события   задается следующим образом:

Важным частным случаем такого пространства является классический способ задания вероятностей, когда количество элементарных исходов конечно и все они имеют одинаковую вероятность. Тогда вероятность любого события определяется как отношение его мощности (т.е. количества элементарных исходов, благоприятствующих данному событию) к общему числу элементарных исходов: . Однако всегда необходимо помнить, что для того, чтобы применять данный способ, необходимо убедиться в том, что элементарные исходы действительно равновероятны. Это должно либо быть сформулировано как исходное условие, либо этот факт следует строго вывести из имеющихся начальных условий.

13.Повотрные независимые испытания.Формула Бернули и ее обобщение.Теория вероятностей имеет дело с такими экспериментами, которые можно повторять, по крайней мере теоретически, неограниченное число раз. Пусть некоторый эксперимент повторяется n раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений часто называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:1)результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей»;2)вероятность «успеха» в каждом последующем испытании не зависит от результатов предыдущих испытаний. Под схемой Бернулли понимают конечную серию n повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают:p=P(Y), а непоявления (неудачи) P(H)=q=1-p . Бернулли установил, что вероятность ровно m успехов в серии из n повторных независимых испытаний вычисляется по следующей формуле: То значение  , при котором число   является максимальным из множества { }, называется наивероятнейшим, и оно удовлетворяет условию np - q     np+ p,  Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из k событий с вероятностью   (i=1,2…k) . Вероятность появления m1 раз первого события и m2  - второго и  -го находится по формуле : . При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

14.ЛТМЛ и ИТМЛ. Функция Лапласа и ее свойства. Локальная теорема Лапласа Пусть проводится n испытаний Бернулли с вероятностью р появления события А в

каждом из них. Пусть при этом n достаточно большое число (n >> 1) и npq ≥ 10 (n – большое, а р – не очень маленькое)

Тогда вероятность, того, что событие А произойдет ровно k раз может быть найдена по приближенной формуле:

Замечание: таблица значений функции ϕ(х ) обычно приводится в задачниках Теории вероятностей.

Свойства функции ϕ(x):

1. ϕ( х) > 0

2. ϕ( -х) = ϕ(х )

3.

Интегральная теорема Лапласа

В условиях локальной теоремы Лапласа вероятность того, что событие А произойдет от k1до k2 раз (k1 ≤ k ≤ k2)

- формула ЛапласаЗамечание: иногда функцией Лапласа называется выражение несколько отличающееся от

написанного.

Свойства функции Лапласа

1. Ф(−х) = Ф(х)

2. Ф(х )- монотонно возрастает

3.

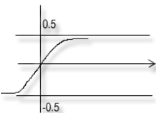интегральная теорема Лапласа

Замечание: функция Лапласа Ф(х) связана с

15.Случайные величины. Определения. Примеры. Экономистам часто в своих исследованиях приходится иметь дело с различными показателями которые в процессе эксперимента ведут себя не предсказуемо. Примеры:Нельзя предсказать к концу рабочего дня ежедневную выручку в магазине,ежемесячный товарооборот; кол-во писем ежедневно приход.на почту, длину очереди в каждой момент времени.Все эти показатели делятся на:1)дискретные – такая случайная величина которая принимает конечное четное число значений(кол-во писем,длина очереди,кол-во бракованных изделий в данной партии,число родившихся детей в течении суток);2)непрерывные – если она своими зн-ми может заполнить сплошь некоторый промежуток(дальность полета артиллерийского снаряда, расход электроэнергии на предприятии за месяц). Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причем появление того или иного значения этой величины до её измерения нельзя точно предсказать.Формальное математическое определение следующее: пусть   — вероятностное пространство, тогда случайной величиной называется функция  , измеримаяотносительно   и борелевской σ-алгебры на  . Вероятностное поведение отдельной (независимо от других) случайной величины полностью описывается её распределением. С.в.- 1)переменная,которая принимает свои значения в зависимости от случая X,Y,Z(X=x),где х – число реализаций случ.велич. в процессе эксперимента. 2)это математическая модель реального показателя.

16.Действия над случайными величинами.Пусть случайная величина Х принимает значения хi с вероятностями Р(Х = xi) =pi(i= 1, 2, ..., п), а случайная величина Y — значения уj с вероятностями Р(Y = у) =pj(j = 1, 2, ..., m). Произведение КХ случайной величины Х на постоянную величину K — это новая случайная величина, которая с теми же вероятностями, что и случайная величина X, принимает значения, равные произведениям на К значений случайной величины X.  Квадрат случайной величины (X 2) — это новая случайная величина, которая с теми же вероятностями, что и случайная величина X, принимает значения, равные квадратам ее значений. Сумма случайных величин Х и Y — это новая случайная величина, принимающая все значения вида xi + уj, (i = 1, 2, .... п; j = 1, 2, ..., т) с вероятностями рij, выражающими вероятность того, что случайная величина Х примет значение xi ,a Y — значение yj, т. е. рij = Р(Х = xi; У = уj) = Р(Х = xi)РX=xi(Y = уi). (1) Если случайные величины Х и Y независимы, то  Аналогично определяются разность и произведение случайных величин Х и Y. Разность случайных величин Х и Y — это новая случайная величина, которая принимает все значе-ния вида хi – уj, а произведение — все значения вида хiуj с вероятностями, определяемыми по формуле (1). Две случайные величины называются независимыми, если закон распределения любой из них меняется от того какие значения принимает др.случайная величина.