33. Функция Лапласа и её вероятностный смысл.

Функция Лапласа тесно связанна с нормальным распределением.

. Вероятностный смысл: Ф(х)=(1/(2))*e^((-x^2)/2). Теорема: значение функции Лапласа в точке х, есть вероятность того, что нормарованная нормальная случ. Вел. хN(0,1) примет своё значение в интервале (-х;х)

P(-x<X<x)=[P(a<X<b)= f(x)dx]= ф(t)dt= (1/((2)))*e^((-t^2)/2) dt=ф(х) ч.т.д. Значение функции Лапласа в точке х.

34. Вычисление вероятности попадания значений нормальной случайной величины в заданный интервал.

Теорема: Вероятность того, что нормальная случайная величина примет свои значения в промежутке (;) вычисляется по формуле: где Ф(x) =  .

Эту формулу называют формулой Лапласа.

Доказательство: Пусть случайная величина X распределена по нормальному закону. Тогда

  .

Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную  . Отсюда  .

Найдем новые пределы интегрирования. Если  , то   , если  , то  . Тогда

Выражение  , входящее в эту формулу, является функцией верхнего предела X, которая называется функцией Лапласа или интегралом вероятностей и обозначается Ф(x). В результате получаем:

Ф — Ф , ч.т.д.

35. Вычисление вероятности заданного отклонения нормальной случайной величины. Правило «трёх сигм».

Вероятность того. Что отклонение нормальной сл.вел. от своего мат. Ожид. По абсолютной величине не будет превосходить заданного положительного числа >0 вычисляется по формуле: P(|X-a|<)=ф(/).

Геометрический смысл теоремы:

Правило «трёх сигм»:

Пусть в формуле: P(|X-a|<)=ф(/), =3, тогда P(|X-a|<3)=ф(3)=0,99731. Отсюда правило «трёх сигм»: Если Х нормальная сл.вел., то все её отклонения от мат. Ожид. К абсолютной величине с вероятностью очень близкой к единице, не привосходит утроенного среднего квадратического отклонения. Геометрический смысл: Если над сл. Вел. Х проводить эксперементы и фиксировать её значения, то с вероятностью 0,9973 можно утверждать, что все её значения будут находиться в промежутке (a-3;a+3). Вероятность того, что вне промежутка 0,0027.

36. Функция распределения нормальной случайной величины.

Теорема: функция распр. Норм. Сл. Вел. Вычисляется по формуле: F(x)=1/2+1/2Ф((x-a)/), где Ф- функция Лапласа.

Доказательство: F(x)=P(X<x)=P(-∞<X<x)=[P(a<x<b)= f(x)dx] = 1/((2)*e^(-((t-a)^2)/(2)dt=[z=(t-a)/; t=a+z; dt=dz; t1=-∞z1=-∞; t2=xz2=(x-a)/]= 1/((2) e^(-(z^2)/2)dz=1/(2) e^(-(z^2)/2)dz=1/(2) e^(-(z^2)/2)dz+1/(2) e^(-(z^2)/2)dz=

=1/((2)*1/2*(2)+1/2*Ф((x-a)/)=1/2+1/2Ф((x-a)/) ч.т.д. Геометрический смысл теоремы: Значение функции F в отмеченной точке х численно равно заштрихованной площади криволинейной трапеции.

37. Мода. Медиана, квантили и процентные точки

Модой М₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

            Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

            Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.

Медианой (Med) случайной величины Х называют такое значение, для которой вероятность того что P(X<Med)=P(X>Med). У любого распределения Med может быть только один.

Med разделяет площадь под кривой на 2 равные части. В случае одно-модального и симметричного распределения mx=Mod=Med.

Значение Хр, уровня Р называется квантилем этой случайной величины, если выполняется равенство: P(x<Xp)=P (1). 0<P<1. F(Xp)=P (2). Геометрический смысл квантиля:

Значение сл.вел Uq называется 100q% (сто кю процентной ) точкой сл. Вел. Если: P(x>Uq)=q; 0<q<1.

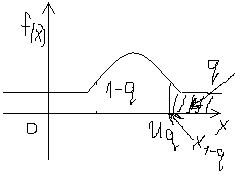
Геометрический смысл: Квантили и % точки существенно используются в мат. Статистике при решении эконом. Задач. Между квантилем и 100q% точкой есть связь: 100q% точка есть квантиль уровня 1-q. Uq=X1-q.

38.Распределения «хи-квадрат», Стьюдента и Фишера. 1)Распределение «хи-квадрат». Пусть имеется несколько нормированных нормально распределенных случайных величин:Х₁, Х₂,…, Х_п (a_i = 0, σ_i = 1). Тогда сумма их квадратов:   

является случайной величиной, распределенной по так называемому закону «хи-квадрат» с     k = n степенями свободы; если же слагаемые связаны каким-либо соотношением (например,  ), то число степеней свободы k = n – 1. Плотность этого распределения: . Здесь   - гамма-функция; в частности, Г(п + 1) = п! . Следовательно, распределение «хи-квадрат» определяется одним параметром – числом степеней свободы k. Замечание 1. С увеличением числа степеней свободы распределение «хи-квадрат» постепенно приближается к нормальному.Замечание 2. С помощью распределения «хи-квадрат» определяются многие другие распределения, встречающиеся на практике, например, распределение случайной величины  - длины случайного вектора (Х₁, Х₂,…, Х_п), координаты которого независимы и распределены по нормальному закону. Распределение Стьюдента. Рассмотрим две независимые случайные величины: Z, имеющую нормальное распределение и нормированную (то есть М( Z) = 0, σ( Z) = 1)  V, распределенную по закону «хи-квадрат» с k степенями свободы. Тогда величина: имеет распределение, называемое t – распределением или распределением Стьюдентас k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Распределение Фишера . Рассмотрим две независимые случайные величины U и V, распределенные по закону «хи-квадрат» со степенями свободы k₁ и k₂ и образуем из них новую величину: . Ее распределение называют распределением Фишера со степенями свободы k₁ и k₂. Плотность его распределения имеет вид: , где   . Таким образом, распределение Фишера определяется двумя параметрами – числами степеней свободы.