•vk.com/club152685050Для проводимого| vk.рассмотренияcom/id446425943 существенным является следующее:
при определении уравнений и граничных условий для случая E>U0 не накладывается никаких условий, приводящих к дискретности значений k и k1. Вследствие этого и спектр собственных значений гамильтониана оказывается непрерывным.
• Итого, спектр собственных значений гамильтониана, совпадающий со спектром энергий стационарных состояний частицы, в присутствии потенциальной ямы конечной глубины состоит из двух частей – дискретной и непрерывной.
• Дискретная часть спектра собственных значений всегда содержит хотя бы одно значение – даже для ямы сколь угодно малых (но конечных) глубины и ширины. Полное число собственных значений конечно.
• Наименьшее из собственных значений соответствует энергии основного состояния частицы в яме. Она всегда больше энергии дна ямы – на величину «энергии нулевых колебаний».
• Дискретным собственным значениям соответствуют локализованные состояния частицы, плотность вероятности которых в основном сосредоточена внутри ямы. Тем не менее, она не обращается в 0 и за ее пределами – кроме как на
бесконечности.
18
•vk.com/club152685050Математически|,vkсостояниям.com/id446425943дискретного спектра гамильтониана соответствуют волновые функции в виде стоячих волн. Плотность вероятности обнаружения частицы в разных точках внутри ямы распределена неравномерно и различным образом для разных состояний.
•Непрерывной части спектра собственных значений гамильтониана соответствуют полностью делокализованные состояния, описываемыми волновыми функциями в виде бегущих волн.
6.8. Стационарные состояния атома водорода: спектр энергий и волновые
vk.com/club152685050 | vk.com/id446425943
функции
Используются материалы из: Фаддeев М.А., Чупрунов Е.В. Лекции по атомной физике (2008, Физматлит).
•Решение методами волновой механики задачи о спектре энергий и стационарных состояниях электронов в водородоподобном атоме представляет особый интерес, поскольку возможно сравнение результата таких вычислений с экспериментальными данными и подтвержденными ими результатами расчетов в модели Бора-Зоммерфельда.
•Для решения этой задачи можно найти собственные значения и собственные
функции гамильтониана для электрона (me, e) в кулоновском поле ядра, описываемом потенциальной функцией вида:
•Вообще говоря, такой подход является приближенным. Ядро является микрообъектом, и его поведение также должно описываться волновой функцией. Точнее, волновая функция атома должна быть функцией координат как электрона, так и ядра.
•Однако обычно ограничиваются тем, что в качестве массы описываемой волновым
уравнением частицы берут приведенную массу (mp – масса ядра):
me mp
• vk.com/club152685050Вид оператора Гамильтона| vk.com/id446425943:
ˆ |
2 |
|
e2 |
|
|
|
|
|
|
|
|
|
H (r ) = − |
2m |
− |
4 0 |
r |
r = |
r |
. |
|
|
|
|
|
, где |
|
|
•Спектр этого оператора и нужно определить, для чего требуется решить уравнение на собственные значения:
ˆ =
H E
• Поскольку потенциальная функция обладает центральной симметрией, используют сферические координаты:
= (r, , ) ,
где оператор Лапласа имеет вид
•С этим лапласианом, решаемое уравнение записывается как:
•Его можно дополнить требованиями однозначности, непрерывности и конечности волновой функции. Таким образом, задача математически сформулирована.
•Какого результата ее решения можно ожидать?
Поvk.com/club152685050аналогии с рассмотренными| vk.com/id446425943ранее случаями, можно ожидать следующего:
•Спектр собственный значений гамильтониана, то есть, спектр энергий стационарных состояний, непрерывен для E>0. Такие состояния в классической физике соответствуют «пролету электрона мимо протона». В волновой механике должны
получиться волновые функции в виде бегущих волн и их пакетов. (Имеются в виду
полные волновые функции с временнόй частью вида exp(–iEt/ħ) )
•Спектр энергий стационарных состояний для E<0 дискретен. Такие состояния локализованы, соответствующие им волновые функции имеют вид стоячих волн.
•Дискретные состояния нумеруются квантовыми числами, принимающими лишь целые значения. Квантовые числа появляются в рассмотрении при установлении граничных условий.
•По аналогии с модами электромагнитных колебаний в кубической полости с проводящими стенками, рассмотренными при выводе формулы Рэлея-Джинса, можно ожидать, что количество независимых квантовых чисел будет равно 3 (равно размерности задачи, т.е. числу пространственных переменных). При этом из-за сферической, а не декартовой симметрии рассматриваемой задачи квантовые числа «неравнозначны», поскольку задаются граничными условиями разных видов
(по r, и ).
Такие ожидания оказываются верными.
• Действительно, как и для электромагнитного поля в кубической полости с
vk.com/club152685050 | vk.com/id446425943
проводящими стенками (при выводе формулы Рэлея-Джинса), решение для волновой функции частицы в кулоновском поле при E<0 оказывается возможным представить в виде произведения трех функций, каждая из которых зависит от одной координаты.
•Принято записывать решение (волновую функцию) в виде произведения радиальной и угловой частей:
При этом угловая часть сама может быть представлена произведением функций азимутального и полярного углов.
•Вид функций-решений задается тремя квантовыми числами: n – главное; l – орбитальное; и m – магнитное квантовое число. Очевидны и справедливы аналогии с квантовыми числами модели Бора-Зоммерфельда.
•Вид угловой части волновой функции определяется квантовыми числами m и l :
•Эти функции имеют название «сферических гармоник», поскольку для
сферических координат играют роль, аналогичную роли гармонических функций
для декартовых координат. |
4 |
|
vk.com/club152685050 | vk.com/id446425943
•Здесь коэффициент k равен m при m 0 и равен 0 при отрицательных m.
•Следующий, корневой множитель – нормировочный. Он появляется, если потребовать, чтобы угловая часть волновой функции имела собственный физический смысл – задавала (квадратом своего модуля) вероятность обнаружить электрон в телесном угле вблизи ( , ). Нормировка – требование, чтобы интеграл от этой величины по полному телесному углу был =1.
•Зависимость от азимутального угла наиболее проста и имеет вид экспоненты мнимого аргумента. Этот множитель не влияет на модуль функции. Поэтому все распределения вероятности симметричны относительно полярной оси.
•Зависимость от полярного угла задается специальными (в математическом смысле) функциями – «присоединенными полиномами Лежандра» 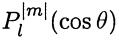 , общий вид которых:
, общий вид которых:
•Несмотря на достаточно сложную форму записи в общем виде, угловые волновые функции для малых значений квантовых чисел в действительности достаточно просты.
vk.com/club152685050 | vk.com/id446425943
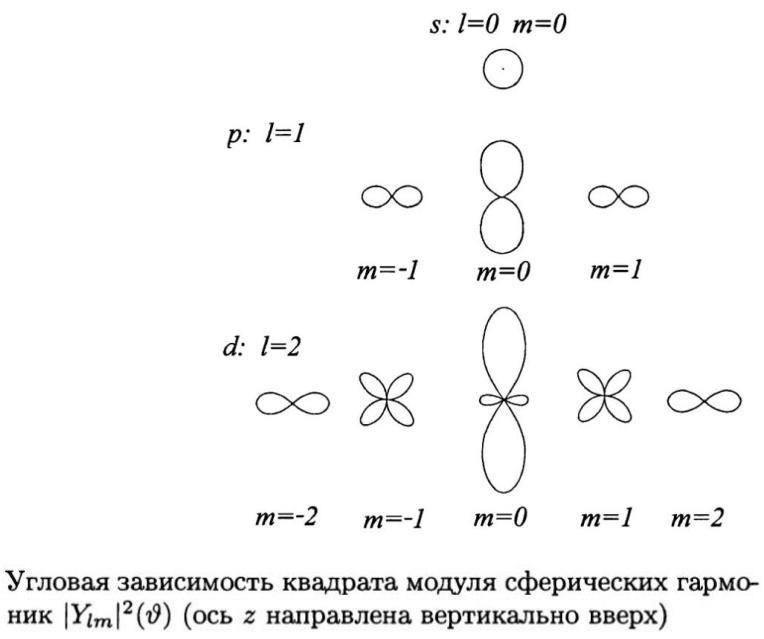
• vk.com/club152685050Здесь те же данные| vk.com/id446425943
представлены в графическом виде.
•Изображены не «электронные облака», а угловые зависимости плотности вероятности в виде полярных диаграмм.
•Трехмерные изображения сферических гармоник (зависимости плотности вероятности от ( , )) представляют собой тела вращения вокруг вертикальной оси.

•vk.com/club152685050Из приведенной|таблицыvk.com/id446425943видно, что:
--состояния принято классифицировать (буквами s, p, d, f и т.д.) в соответствии со значением орбитального квантового числа l =0,1,2,3 …;
--тем не менее, значение орбитального квантового числа не полностью определяет зависимость плотности вероятности от полярного угла – на него
влияет и значение магнитного квантового числа m.
•Математически, орбитальное квантовое число l появляется в связи с требованием
ограниченности угловой части волновой функции. При целых l=0,1,2… решениями соответствующего уравнения являются полиномы Лежандра, при нецелых – решения неограниченны.
•Магнитное квантовое число m отражает требование непрерывности и однозначности волновой функции вблизи границ диапазона изменения
азимутальной координаты .
Имеем: ~exp(im ).
Требуется, чтобы значения функции и ее производной на границах области определения ( =0 и =2 ) совпадали, поскольку эти границы физически соответствуют одному направлению. Это требование выполняется при целых m.
•Решения уравнения для полярной координаты в виде полиномов Лежандра существуют лишь для m l . То есть, диапазон изменения m:







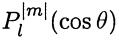 , общий вид которых:
, общий вид которых: