Геометрическое определение вероятности.

Если - некоторое непустое квадрируемое множество точек плоскости, - подмножество , то по определению

.

Аналогично формулируется геометрическое определение вероятности для прямой и для трехмерного пространства.

Частота события. Если опыт, в результате которого наблюдается событие , повторяется в одинаковых условиях раз и событие при этом наступило раз, то отношение называется относительной частотой события ( - называется частотой ). Частота (относительная) имеет свойство стабилизироваться при .

Статистической вероятностью события называется число, около которого стабилизируется относительная частота этого события, т.е. при достаточно большом числе повторений опыта.

Под схемой Бернулли понимают - кратное повторение опыта, имеющего два исхода – успех и неудача ( и ), причем вероятность успеха и вероятность неудачи от опыта к опыту не изменяются, то есть и независят от номера опыта. Основная задача, которая возникает в схеме Бернулли следующая: дано и , требуется найти вероятность того, что в повторениях опыта успех наступит в точности раз. Эта задача решается по формуле Бернулли:

.

Наиболее вероятное число успехов (мода) находится из двойного неравенства , из которого следует правило:

если - не целое, то ,

если же - целое, то имеет два значения и .

Формулу Бернулли называют еще биномиальной в силу того, что правая часть этой формулы является общим членом разложения по формуле Ньютона

.

Обозначим вероятность того, что в опытах схемы Бернулли успех наступит от до раз, символом . Тогда

.

Первое обобщение схемы Бернулли. Опыт повторяется раз, вероятность успеха в -том опыте равна - вероятность неудачи в -том опыте. Требуется, найти вероятность того, что в опытах успех наступит раз (неудача - раза). Для решения этой задачи вводят производящую функцию - многочлен от переменной :

.

Если раскрыть все скобки, то получится:

,

т.е. искомая вероятность является коэффициентом при .

Второе обобщение схемы Бернулли. Повторяется опыт раз, причем при каждом повторении опыт имеет исходов с вероятностями , которые от опыта к опыту не изменяются и . Требуется найти вероятность того, что исход наступит раз . Обозначим эту вероятность через . Тогда справедлива, так называемая, полиномиальная формула Бернулли:

.

Очевидно, что при полиномиальная формула превращается в формулу Бернулли (биномиальная формула).

При больших имеет место асимптотически приближенная формула (локальная приближенная формула Муавра-Лапласа)

.

Функция табулирована (см.приложение 1). При больших имеет место асимптотически приближенная формула (интегральная приближенная формула Муавра-Лапласа)

,

где 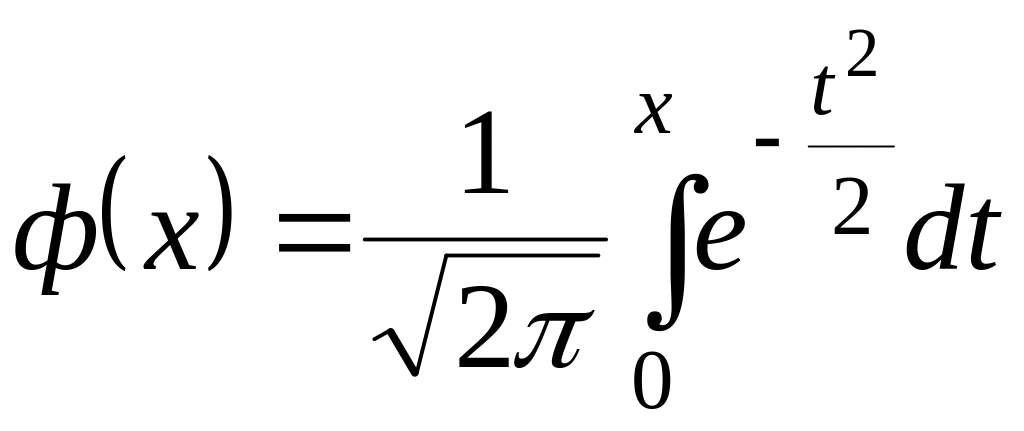(функция Лапласа). Функцию Лапласа называют еще интегралом вероятности, она так же табулирована (см. приложение 1).

При больших и малых таких, что имеет место асимптотически приближенная формула Пуассона

.

Функция табулирована для некоторых наиболее часто встречающихся значений (см.приложение 3).

Формулу Пуассона называют формулой для редких событий из-за того, что - мала.

Случайная величина называется дискретной (прерывной), если она может принимать только конечное или бесконечное, но счетное множество значений с вероятностями , причем, ясно, что . Закон распределения , как правило, записывается в виде таблицы, которая называется еще рядом распределения

				…

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в системе координат строят точки и соединяют их последовательно отрезками прямых и из крайних точек опускают перпендикуляры к оси абсцисс. Получающийся при этом многоугольник называется многоугольником распределения.

Математическим ожиданием (средним значением) дискретной случайной величины называется число

,

где в случае, когда может принимать счетное множество значений , ряд

должен быть абсолютно сходящимся.

Дисперсия дискретной случайной величины равна

,

а среднее квадратическое отклонение равно .

Вероятность неравенства находят по формуле

Функцией распределения дискретной случайной величины называется функция , которая определяется формулой

Имеет место формула

Если произвольная случайная величина, то , , называется функцией распределения . Функция распределения любой случайной величины непрерывна слева в любой точке.

Если функция распределения случайной величины непрерывна всюду на , то случайная величина называется непрерывной. Для непрерывной случайной величины при любом .

Если дифференцируема всюду на за исключением, быть может, конечного числа точек в любом конечном промежутке, то называется плотностью распределения вероятностей случайной величины .

Если непрерывная случайная величина, то

Функция распределения выражается через плотность распределения вероятностей по формуле .

Имеет место формула .

Для случайных величин, имеющих плотность распределения вероятностей , математическое ожидание , диспресия определяются по формулам:

.

Среднее квадратическое отклонение .

Характеристические свойства функции распределения:

­ непрерывна слева в любой точке;

.

Для системы двух случайных величин функция распределения определяется по формуле . Плотность распределения вероятностей определяется по формуле .

Если - область на плоскости, то

Плотности распределения вероятностей случайных координат и системы выражаются через по формулам

.

Корреляционным моментом или ковариацией случайной точки называется число

Коэффициент корреляции между координатами и системы определяется по формуле

.

Примеры часто встречающихся законов распределения дискретных случайных величин.

Биномиальный закон распределения. Параметры ;

;

.

Пуассоновский закон распределения.

Параметр

.

Геометрический закон распределения.

Параметр

.

Если и , то закон распределения . Называется сдвинутым геометрическим. Тогда .

Гипергеометрический закон распределения.

Пусть . Если возможными значениями случайной величены являются , а соответствующие вероятности определяются по формуле

,

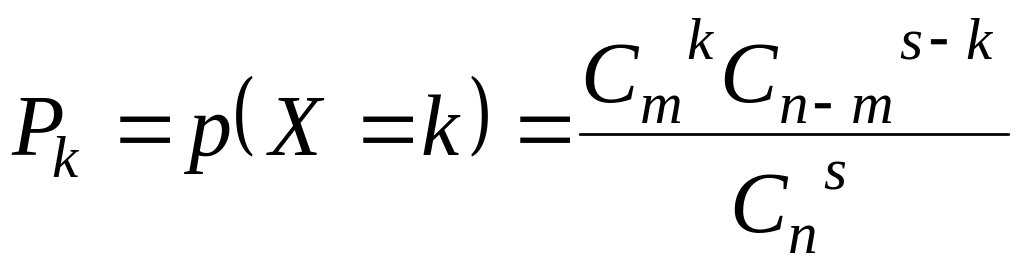то говорят, что имеет гипергеометрический закон распределения, - параметры.

Примеры наиболее часто встречающихся законов распределения непрерывных случайных величин.

Нормальный закон распределения (закон Гаусса). Параметры - может принимать любое действительное значение. Плотность распределения вероятностей

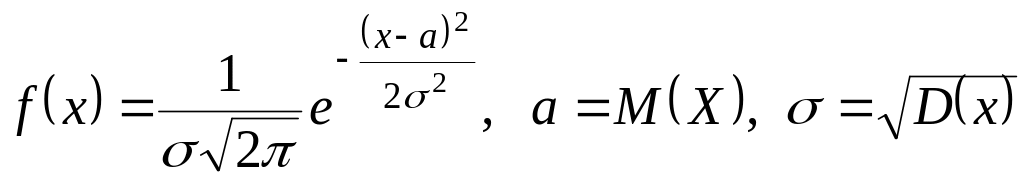
Функция распределения выражается через функцию Лапласа

.

Равномерный закон распределения на отрезке . Возможные значения , плотностьраспределения вероятностей

.

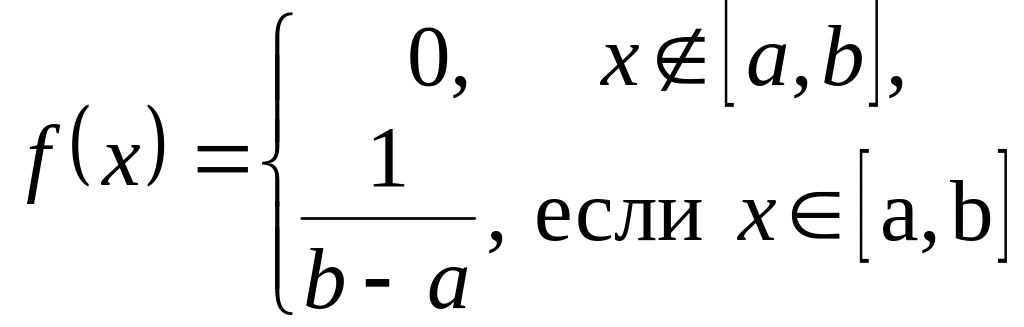Функция распределения

.

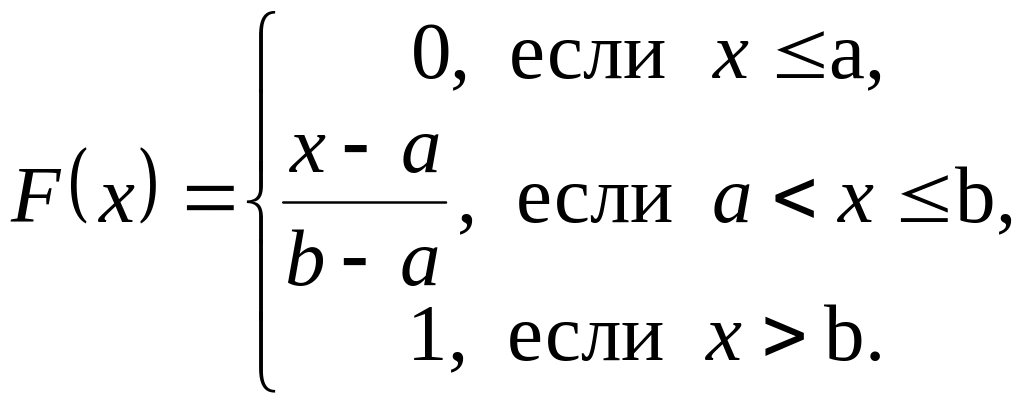
Показательный закон распределения. может принимать любое неотрицательное действительное значение. Параметр .

Плотность распределения вероятностей и функция распределения задаются формулами:

.