2 2 . Граф, маршруты в графе, компоненты связности, связные графы.

Г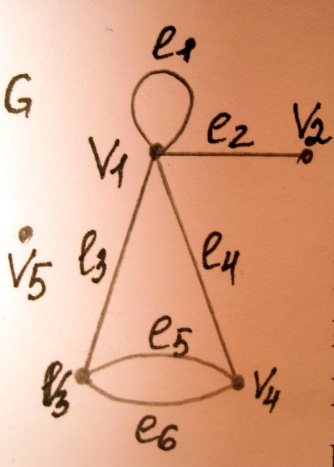 раф – геометрическая фигура, состоящая из мн-ва точек, соединенных непрерывными линиями.

Точки - вершины, линии – ребра.

Ex: G=(V,E) – граф, где V – мн-во вершин, Е – мн-во ребер.

Если 2 вершины соединены ребром, то это ребро инцидентно данным вершинам (ребро e2 инцидентно вершинамV1 и V2).

Вершины наз. смежными, если существует инцидентное им ребро (V1 и V2).

Ребра наз. кратными, если они инцидентны одним и тем же вершинам (e5,e6)

Вершина, кот не инцидентно ни одно из ребер, наз. изолированной.(V5)

Ребро, соединяющие вершину саму с собой, наз. петлей (e1).

Граф, не содержащий петель и кратных ребер, наз. обыкновенным графом.

Г раф G′ = (V′,E′) наз. подграфом графа G = (V,E), если: а) V′ ≤ V, E′ ≤ E

б) ребро eЄE′ и е инцидентно в графе G вершинам х и у, то х,у Є V′

E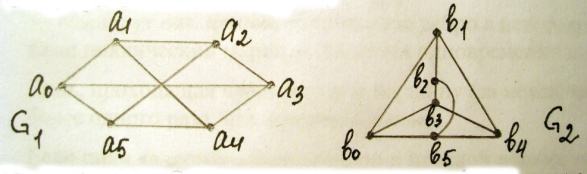 x: Граф G2 является подграфом графа G1, а граф G3 не является.

Г раф G1 = (V1, E1) наз. изоморфным графу G2 = (V2, E2), если существует биекция f: V1→V2 такая, что для любых вершин х, уєV1 число ребер из Е1, инцидентных этим вершинам, равно числу ребер из Е2, инцидентных вершинам f(x) и f(у).

Ex: Графы G1 и G2 изоморфны.

Ех: Графы G3 и G4 не изоморфны, т.к. в графе G3 три вершины, смежные вершине а1, а в графе G4 две вершины, смежных вершине b1.

Маршрутом в графе G наз. последовательность ребер е1, е2, …., еk, для которой существует последовательность вершин v0,v1,….,vk такая что е1 инцидентно v0 и v1, е2 инцидентно v1 и v2, …еk инцидентно v(k-1)и vk.. Вершина v0 наз. началом маршрута, vk – концом.

Маршрут наз. циклическим, если v0 = vk.

Ex: f1, f2, f3, f4, f6 – с началом в вершине а1 и концом в вершине а6.

f2, f3, f4, f7 – циклический маршрут с началом и концом в вершине а3.

Маршрут, в кот. ребра не повторяются, наз. цепью. Ex: f1, f7, f4, f3, f5, f6

Циклический маршрут, в кот. ребра не повторяются, наз. циклом. Ex: f7, f4, f3, f5, f6, f8

Цепь, проходящая через каждую вершину (за исключением начальной и конечной) не более одного раза, наз. простой цепью. Ex: f1, f7, f6, f9

Цикл, проходящий по разным вершинам (за исключением начальной и конечной), наз. простым циклом. Ex: f2, f5, f6, f8

П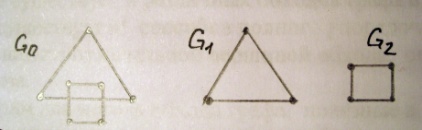 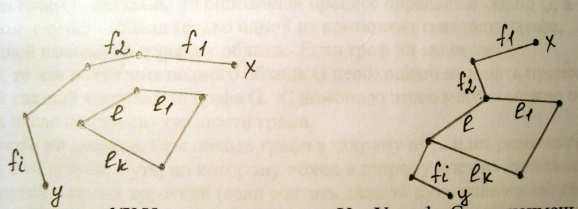усть вершина u – начальная вершина, v – конечная вершина, тогда (u,v) – маршрут.

Теорема: если u и v – различные вершины графа G и существует (u,v) – маршрут, то существует и простая (u,v) – цепь. Если граф содержит цикл, то он содержит и простой цикл.

Длиной маршрута наз. количество ребер

Расстоянием d(u, v) м/у различными вершинами (u, v) графа G наз. наименьшее число ребер (u, v)-цепи, если существует (u, v) – цепь. Если же вершины U и V не соединены цепью, то d(u, v) = ∞. Для любой вершины d(u, v) = 0.

Вершины u и v наз. связанными, если существует (u,v) – цепь. Каждая вершина связана сама с собой.

Отношение связанности является отношением эквивалентности, т.е. оно рефлексивно, симметрично и транзитивно.

Классы разбиения, соответствующие отношению связанности, наз. компонентами связности. Ех: Граф G0 имеет 2 компоненты связности: графы G1 и G2.

Граф, состоящий из одной компоненты связности наз. связным графом (т.е. это граф, любые две различные вершин которого соединены цепью).

Теорема о разрыве цикла: Если в связном графе удалить ребро, принадлежащее циклу, то граф останется связным.