24. Тригонометрический ряд Фурье.

Опр. Ф- циональный ряд вида : a₀/2 _{+ (1)}

где a₀,a_n,b_n (n=0,1,2,…) /R, наз. тригонометрическим рядом. Указ. числа наз. его коэффициентами. Допустим, что ряд(1) на отрезке [ ] равномерно сходиться к ф-ции f(x).

f(x)= a₀/2 _{+ (2)} поскольку члены ряда (2) явл. непрер. ф-циями, этот ряд - равномерно сходящийся к ф-ции f(x), то сама f(x) явл. непрерывной(св-во 1. б.19)и этот ряд почленно интегрировать. Проинтегрировав почленно ряд (2) на [ ] получим

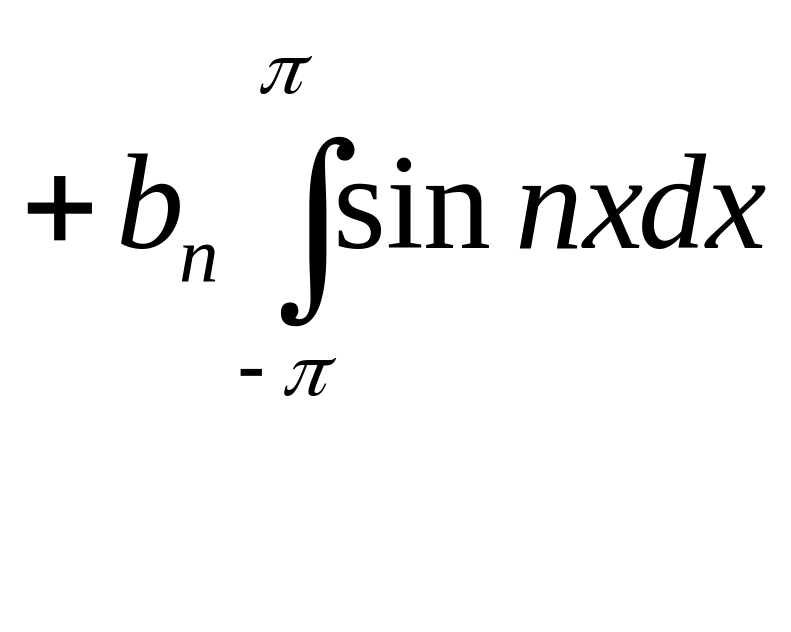. Поскольку

(n=1,2,…). Получим _{=a0 =>a0=1/}

(3). Домножим обе части р-ва (2) на cos kx и проинтегрируем получ. ряд на _{[ ]:} (4) Поскольку

_(k≠n),

( k). Из р-ва (4) при n=k получим:

_{an (5).}

Аналогично, помножив (4) на sin kx и проинтегрировав получ. ряд на [ ] найдем коэффициент _bn=1/ (6).

Опр.пусть f(x) интегрируемая ф-кция на [ ]. Числа a₀,a_n,b_n, кот. опр. ф-лами (3),(5),(6) наз. коэффиц. Фурье ф-кции f(x). Тригон. ряд (1), коэфф. которого явл. коэф-тами Фурье ф-кции f(x), наз. рядом Фурье этой ф-кции. Его обозн. :

f(x) a₀/2+

(7). Знак соответствия озн., что интегрируемой на[ ] в виде равномерно сход. на этом отрезке тригон ряда, то этот ряд единственный и явл. рядом Фурье. Док-й результат можно так : Теорема 1 Если f(x) можно предст. на отрезке [ ] в виде равномерно сход. на этом отрезке тригон. ряда , то этот ряд единственный и явл. рядом Фурье. Теорема 2( дост. условие представления ф-кции черз её ряд Фурье) : Пусть периодич. ф-кция f(x) с периодом явл. кусочно-монотон. и огран на [ ] ,тогда ряд Фурье f(x) явл. сходящимся на всей числ. оси. Сумма S(x) найденного ряда равна значению ф-кции f(x) во всех т. непр-сти ф-кции f(x) , если x₀ – точка разрыва ф-кции f(x), то S(x)=(f(x₀-0)+f(x₀+0))/2, т.е. сумма ряда Фурье в т. х_о равна среднему арифм. одностор. пределов ф-кции в т. х_о. В кончных точках отрезка[ ] сумма ряда Фурье принимает значения . Замечание если ряд Фурье сходится к S(x) то эта явл. периодической, так как периодическими явл. все члены ряда (2). Если ряд (2) сходящийся к f(x) на [ ] то он сходится к этой ф-кции на всей числовой оси, при этом f(x+ )=f(x). Таким образом заданную на [ ] ф-кцию можно периодически продолжить на всю числ. прямую и представить в виде суммы ряда Фурье. 2. Произв. - периодическую ф-кцию φ(х) можно проинтегр. по периоду

_, т. _(- . Поэтому коэфф. ряда Фурье можно найти вычисляя интегралы (3),(5),(6) на отрезке длиной :

25. Ряды Фурье для функций четных и нечетных. Ряды Фурье для 2l периодических функций. Примеры.

Заметим что условия, кот. накладываются на f(x) при разложении его в ряд Фурье

значительно проще,чем при его разложении в степ. ряд.Действительно ,при разложении

ф-ии в ряд Тейлора необх.чтобы она была не только непрерывной но и бескон.число раз

диффер-ема .Это совсем необходимо это совсем не необх.для разлож.ф-ии в ряд Фурье

Согласно теор.2 (24),если ф-ия непрер. на отрезке и если она имеет конечное кол-во

точек розрыва 1-го рода на отрезке ,ее можно предст. рядом Фурье.Таким образом,класс ф-й

,кот.можно разлож. в ряд Фурье,значительно шире чем класс ф-й ,кот. можно разлож. в ряд Тейлора.

Пусть f(x) на можно разл. в ряд Фурье . Покажем что вычисл. коэф.этого ряда значит. упрощатся в случае ,если f(x) четная или нечтная

Если f(x) четная ,ее ряд Фурье f(x)= a_o/2 _{+ ,где ao=2/ f(x)dx , an=}

_{=2/ f(x) cosnx dx,n=1,2…}

Если f(x)-нечетная ,ее ряд Фурье _{f(x)= bn sin n x ,где bn=2/ f(x) sin nx dx}

n=1,2… Действительно ,если (x) интегр.на [- L;L], ( L>0) и четная ,то _{(x)dx= (x)dx.} Если (x)-нечетная , (x)dx =0. График:

Замечание: ф-лы (1),(2) отображ. характер f(x).Если f(x) четн.ее ряд Фурье содерж.только

косинусы (четные).Если f(x) нечетная ее ряд содерж.только синусы (нечетные) График:

Пример:Разложить в ряд Фурье 2 -периодичес- кую ф-ию:f(x)= ,

Эта ф-ия кусочно –монотонная поэтому ее можно разложить в ряд Фурье .Поскольку

ф-ия четная находим ее коэф. по формуле _{(1): ao=2/ xdx =} ;

_{an=2/ x cosnxdx=} =2/ (xsin nx/n -_1/n

=2/ cos nx =2/ ((-1)ⁿ-1)

_{= ((-1)}ⁿ_-1)

_cosnx=

Пусть ф-ия f(x) кусочно-монотонная на ,(L>0) и есть 2L-периодическая

разложим его в ряд Фурье.Сделаем замену переме- нной x=2L/ .Рассм. =f(2L/ )

ф-ия кусочно-монотонная на и также есть 2 -периодическая.

Ряд Фурье для =a₀/2+ (3)

(4)

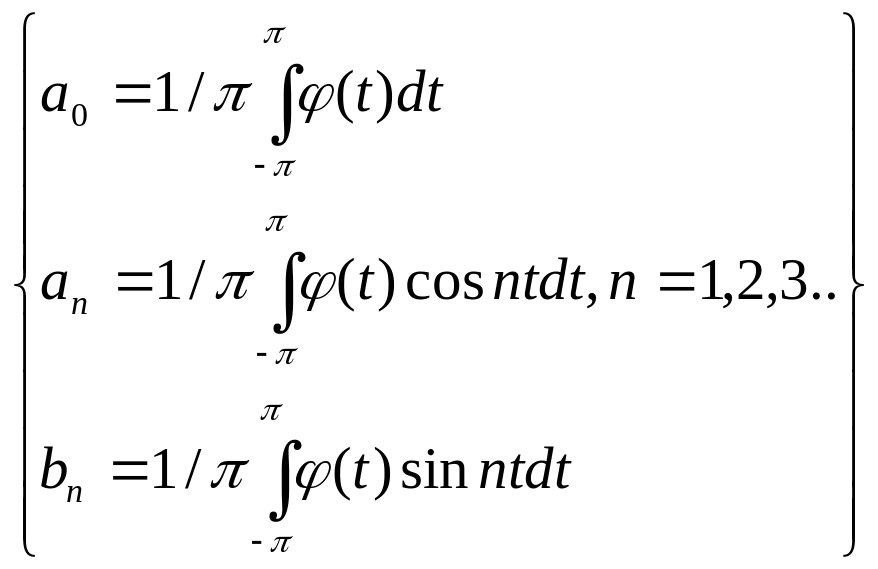
Bернемся к переменной x в фомулах (3),(4) возьмем t= .Получим :f(x)=a (5)

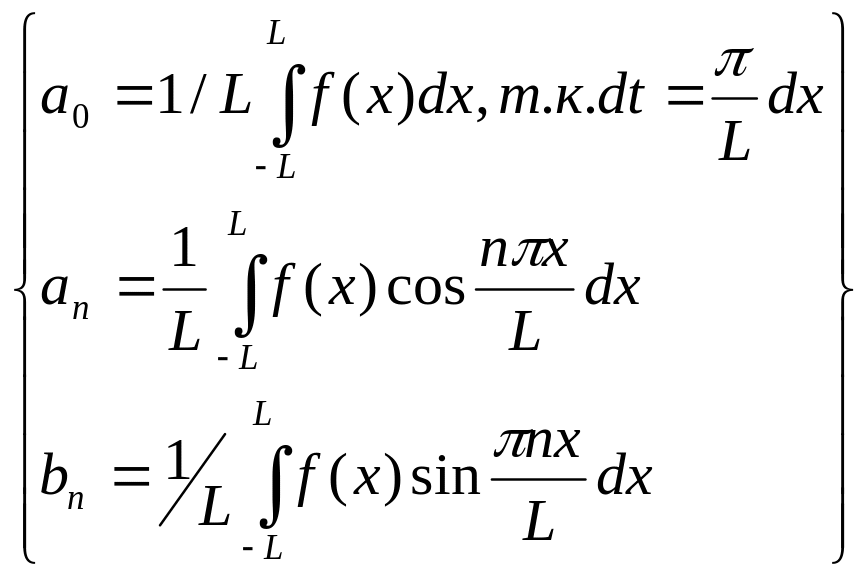(6) Ряд (5)-ряд Фу рье для f(x) c периодом 2L.Его коэф. наход. по ф-ле (6).

Замечание: все теоремы которые справедливы для рядов Фурье 2 -период. фий, сохр. и для рядов Фурье 2L-периодических ф-ий.