30. Обчислення потрійного інтегралу. Приклади.

Як і у випадку подвійного інтегралів обчис. Потрійного інтегралів зводиться до обчислення поверхні інтегралів, тобто до інтегрування по кожній змінній окремо. Нехай область G обмежина знизу і зверху поверхнями він повідно z=псі1(x,y) z=псі2(x,y)

Тут долженб іть графік

Означення. Назвимо область G правельною напрямі осі OZ, якщо кожна пряма , що проходить через внутріщно перетинає межу області G у двох точках. Позначимо через Gотx,y проекцію області G на координатну площину xoy, тоді для будь якої неперервної в області G функція U=f(x,y,z)справедлива формула SSSпо G від f(x,y,z)dxdydz =” ”(1)Зміст формули (1) який треба спочатку обчислити інтегр. Він псі1 (x,y) до псі2(x,y) “ ”

По змінній z, вважаючи зміні x,y сталими нижнею і верхн. Межею інтегр. Тут є рівняння відповідно нижнєю і верхнєю поверхні що обмежують область G, в наслідок цього одержимо функцію I(x,y) якщо він цієї функц. По області Gxy за відомими правилами обчислити подвійн. Інтеграл по y результаті одержимо значення необх. Потрійн. Інтеграл.

Заув.1)Як правило межі внутрішн. Звич.інтегралу є зміними вони залежать він цих змінних що не є в цьому інтегралі змішн. Інтегрування. Обидві межі інтегрування будуть сталими тільки у тому випадку якщо область інтегр. G, є прямий циліндр ” ” якого паралельні осі oz, а осн. Знаходят. Площині xoy.2)Порядок інтегр. У формулі (1) може бути і іншими, тобто зміні x,y,z у правій частині формули (1) за певних умов можна міняти мі тами.Наприклад.Якщо область G правельна у напрямі осі ox I x=фі1(y,z) x=фі2(y,z) рівняння повер. Що обмежують область G при чьому фі1(y,z)<= x<=фі2(y,z), то формулу (1) можна записати у вигляді SSS по G f(x,y,z) dxdydz=SSS по Gyx dydzS” ”

Де Gxy проекція області.

3) У випадку коли область інтегрув. G має більш складний вигляд, тобто не є правільною у напрямі всіх трьох координих осей ox,oy,oz її треба розбити неперервними поверхнями на частиній ” ” з яких буде правильно у напрямі деякої коорд. Осі обчислюючи потрійн.інтеграл він цих частичн. Областей с додаючи одержані велечини за властив.(5) потрійн. Інтегр. Одержимо необчідн. Потрійний інтеграл у області G.

Приклад. Обчислити потр. Інтеграл по G від SSS по G f(x,y,z)z dxdydz де область G обмежина поверхнями z=0,x=0,y=0,x+y+z=1 Проєкцію G(x,y)області G на площину xoy є трикутник обменний у площині xoy прямими x=0,y=0,x+y=1 за формулою (1)маємо

31. Заміна зміних у потрійному інтегралі.

Нехай в замкненій обмеженій області G що належить R³ U=f(X,Y,Z) і Y за формулами [X=X(U,V,W) Y=Y(U,V,W) Z=Z(U,V,W)](1)

Треба перейти до нових змінних інтегрування U,V,W.

Будемо вважати , що область G при переході до нових змінних перетворюється на замкнену обмежену область G* причому функції (1) мають неперервні частинні похідні в області G* і відмінній від 0 фyнк-ний визначник:

  

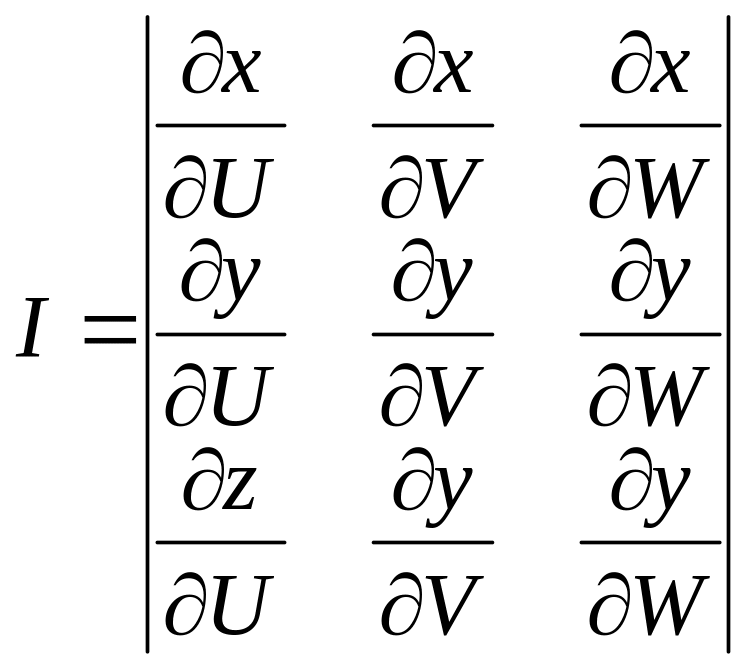
Будемо вважати крім того, що функція f(x,y,z) – неперервна по області G тоді справедлива формула (2)

При розвязанні задаччі найбільш часто зустрічаються циліндричні та сферичні системи координат. Розглянемо який вигляд має ф-ла(2) у таких координатах:

0    2

0    +

-  z  +

Перехід від Декартових координат до циліндричних виконується за ф-лою

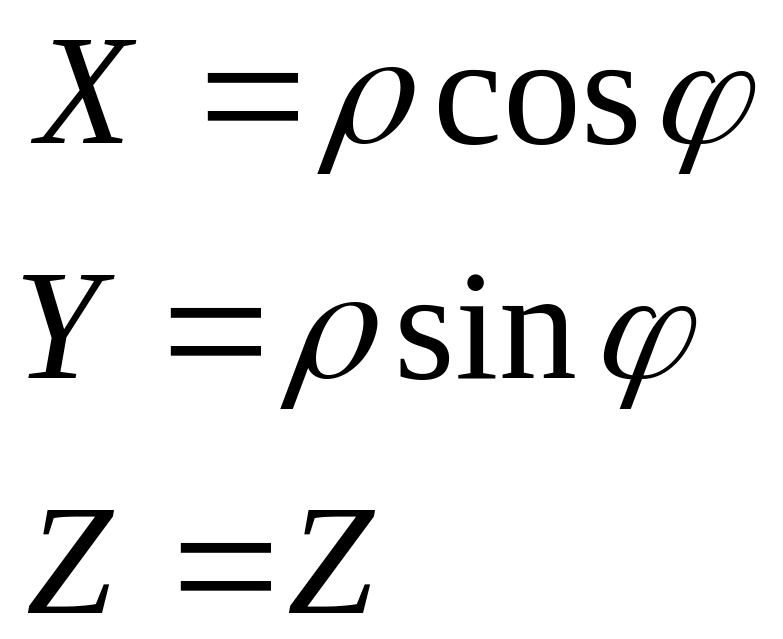
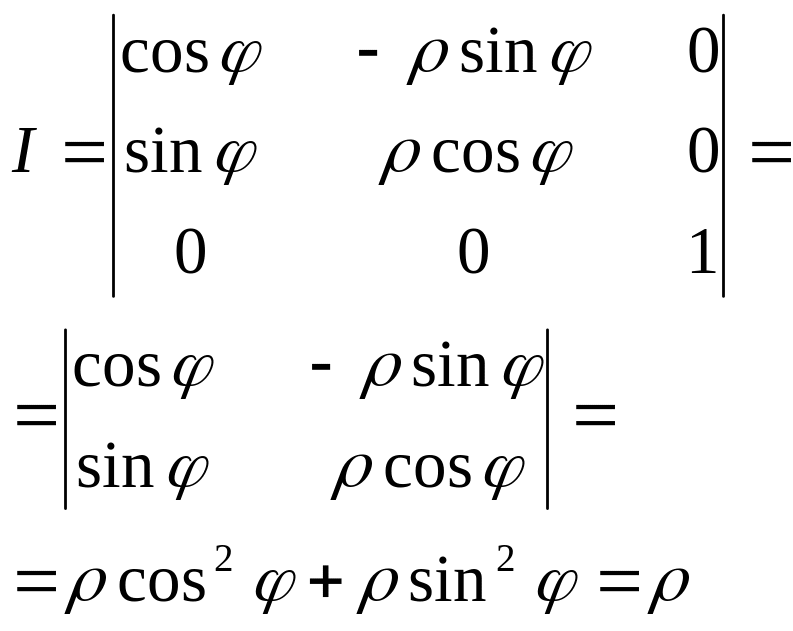
(3)

Назва циліндричній координати повязана з тим що рівні поверхні =const в цих координатах на точках є циліндр, твірні якого паралельні осі OZ:

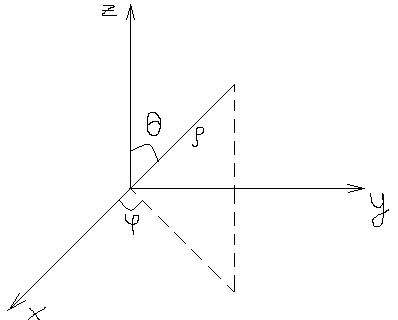
Перехід від Декартовіх координат до сферичних здійснюється за ф-лами :

X=sincos

Y=sin sin

Z=cos

0+

02

0

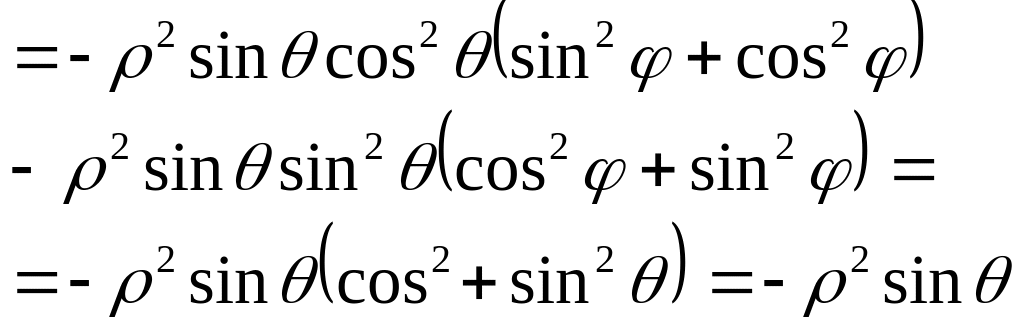
Звідси і формулу (1) можна записати у вигляді

_*

(4)

Зауваження: Назва сферичні координати повязані з тим, що координатна поверхння є сферичною.

Зокрема, якщо обл. G обмежена циліндричною поверхнею

та площинами , то всі межі інтегрування в циліндричних координатах будуть сталими, тобто потрійний інтеграл:

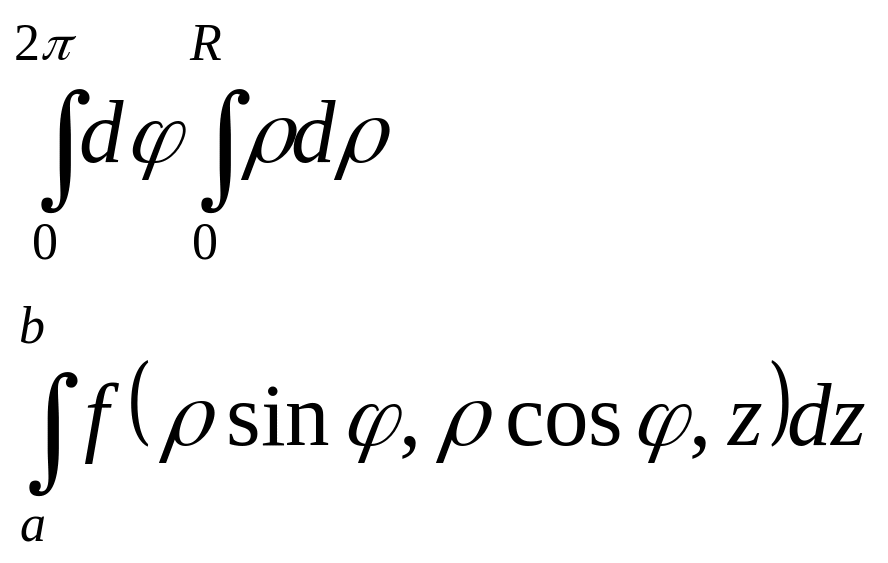
Те ж саме буде і в сферичних координатах у випадку , коли обл. G – куля, або кульове кільце

x²+y²+z² = ²sin²cos² + ²sin²sin²+²cos²=²(sin²(cos²+sin²)+cos²) R R

У випадку коли G – кульове кільце: r²x²+y²+z²R² 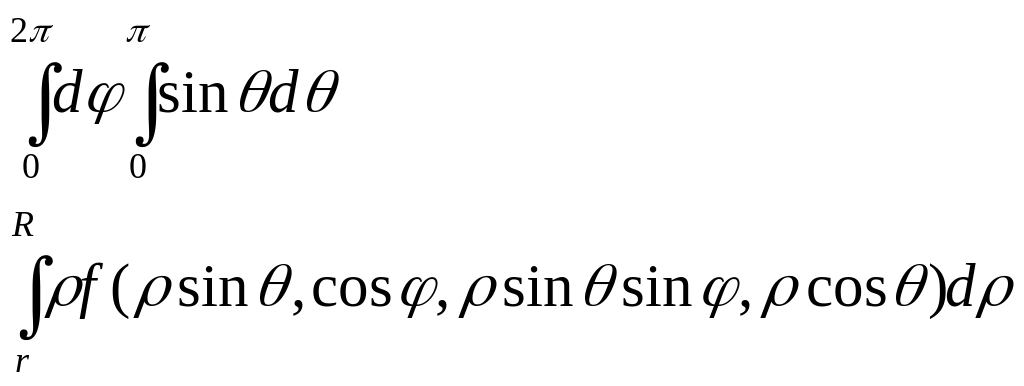Якщо G – куля то в ф-лі [5] r треба взяти r = 0. Загальних правил, коли треба переходити до тої або іншої системи координат не існує, тому часто потрібно записувати інтеграл у різних системах координат і лише потім вирішувати в якій із них обчислювати.

Приклад: обчислити потр інт

де G-куля  1 За ф-лами [5], поклавши

r = 0 , одержимо
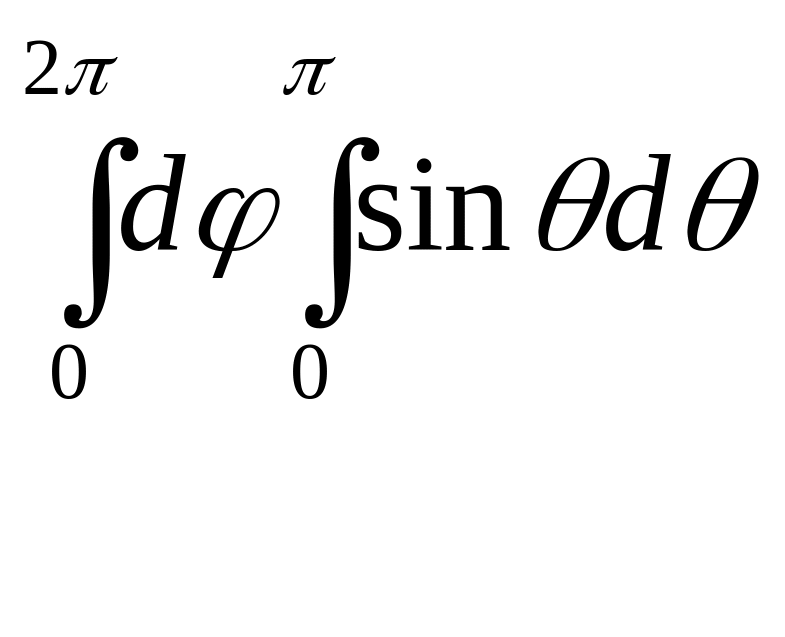