
- •19.Функціональні ряди поняття рівномірной збыжн. Озн вейерштр.
- •20. Поняття степеневого ряду. Теорема Абелья. Інтервал та радіус збіжності степеневого ряду.
- •Теорема2(Абелья) Якщо ряд (1) розбіжний в точці то він буде розбіжним для всіх
- •21. Схема исследования области сходимости степ. Ряда. Примеры. Свойства степ. Рядов
- •22. Ряд Тейлора
- •23. Разложение элементарн. Функций в ряд Макларена
- •24. Тригонометрический ряд Фурье.
- •25. Ряды Фурье для функций четных и нечетных. Ряды Фурье для 2l периодических функций. Примеры.
- •26. Подвійний інтеграл умови його існування і властивості
- •28. Заміна змінних в подвійному інтегралі.Подвійний інтеграл у полярних координатах.
- •29. Поняття потрійного інтегралу. Умови його існування та властивості.
- •30. Обчислення потрійного інтегралу. Приклади.
- •31. Заміна зміних у потрійному інтегралі.
- •32. Криволінійні інтеграли. Приклади.
- •33. Деякі застосування кратних та криволінійних інтегралів.
32. Криволінійні інтеграли. Приклади.
Озн.:Неперервна крива x=x(t),y=y(t),де а<=t<=b наз. гладкою, якщо ф-ція x(t) і y(t) мають неперервні похідні, які не дорівнюють одночасно 0 ні в якій точці a<=t<=b
Озн:Крива LCR2 наз. Кусково гладкою, якщо вона склад. із скінченого числа гладких кривих.
Нех. в площ. хОу задана кусково гладка крива АВ і нехай на цій кривій визначена обмежена ф-ція F(x,y). Розіб’ємо криву АВ точками А=А0, А1,А2,...,Ап =В на n частин.
На кожній з дуг Аi-1Аi, i=1,n Виберемо довільну точку Мi(ﻉi ,ηi )дуги Ai-1Ai і складемо сумую
![]() (1)
(1)
Озн: сума(1) наз. інтегральною сумою ф-ції f(x,y), по кривій
Позначемо через λ=max з li (найбільша з двох дуг Аi-1 Ai 1≤i≤n), якщо при λ→0 існує скінч. границя інтег. суми (1), яка не залежить від способу розбиття кривої АВ на дуги точками Аi
i=0,n
та не залеж. від точок вибору Мi
, i=1,n,
то цю границю наз. кринолін. інтег.
першого роду від ф-ції f(x,y).
![]()
 (2)
(2)
якщо границя (2) існує, то ф-цію f(x,y) назю інтегрованою на кривій АВ. Саму криву АВ наз контуром інтегрування. А наз. начальной тч. інтег., В – конечной
Обчислення криволінійних інтегралів I роду:
крива АВ задана параметрично x=x(t) y=y(t), a≤t≤b, причому ф-ції x(t), y(t) – неперервні разом із своїми похідними, тоді інт. по АВ
![]()
![]()
АВ задана в явному виді y=y(x), a≤x≤b. Тоді крив. інт.
![]()
![]()
леше вваж., що ф-ція у=у(х) – неперервне разом із своєю похідною y’(x).
3) АВ задане рівн. х=х(у), с≤у≤d. Ми вважаємо, що ф-ція х(у) – неперервна разом зі
своєю похідною x’(y), тоді
![]()
![]() Приклад:
обчислити
Приклад:
обчислити
![]() , АВ: у=х3/4, А(0,0), В(4,3)
, АВ: у=х3/4, А(0,0), В(4,3)
![]()
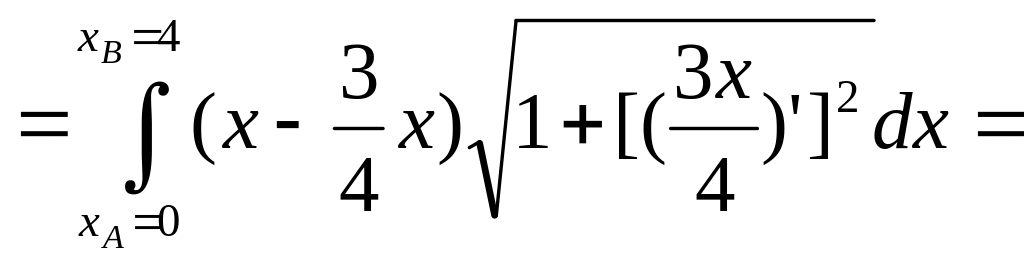
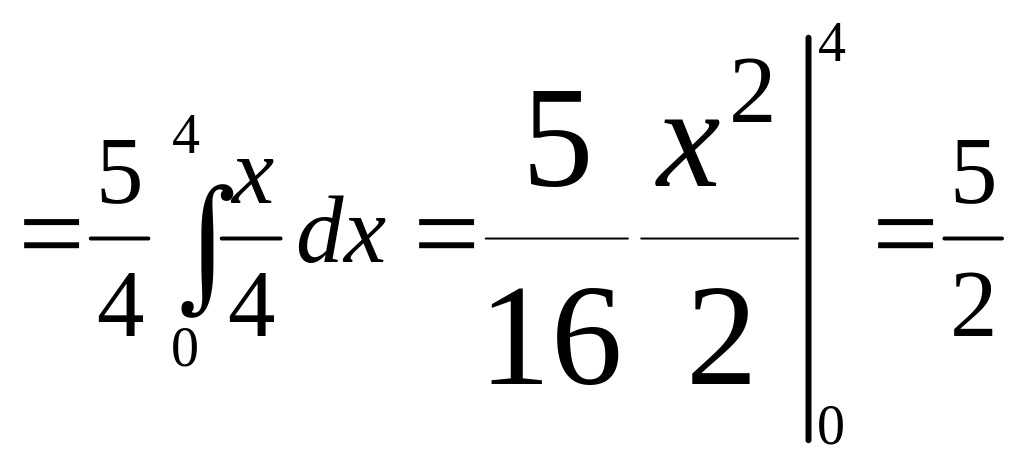 Криволінійні
інтеграли
II
роду визначаються майже так само, як і
криволінійні
інтеграли
I
роду. Нех. в площ. хОу задана кусково
гладка крива А – поч. і В – кін. кривої.
Розіб’ємо на дуги А=А0,А1,...,Аn=В,
на кожній з дуг Аi-1Аi
виберем точку Мi
(ξi,ηi).
Познач. через ⌂хi
проекцію
вектора Аi-1Аi
на вісь Ox.
Криволінійні
інтеграли
II
роду визначаються майже так само, як і
криволінійні
інтеграли
I
роду. Нех. в площ. хОу задана кусково
гладка крива А – поч. і В – кін. кривої.
Розіб’ємо на дуги А=А0,А1,...,Аn=В,
на кожній з дуг Аi-1Аi
виберем точку Мi
(ξi,ηi).
Познач. через ⌂хi
проекцію
вектора Аi-1Аi
на вісь Ox.
Нех. f(x,y)
обмеж. ф-ція, задана на кривій АВ. Розгул.
інт. суму
![]() (3)
(3)
Зрозуміло, що інт. суми в ф-ях (2) і (3) – різні
Озн. Границя при
![]() інтегральних сум в випадку, коли вона
скінченна не залежить від способу
розбиття кривої АВ не дуги точкам
Аi(=0,n)
і вибору точок Mi(i=1,n)
наз. криволінійним
інтег.
від ф-ції f(x,y)
II
роду по координаті х і позначається
символом
інтегральних сум в випадку, коли вона
скінченна не залежить від способу
розбиття кривої АВ не дуги точкам
Аi(=0,n)
і вибору точок Mi(i=1,n)
наз. криволінійним
інтег.
від ф-ції f(x,y)
II
роду по координаті х і позначається
символом
![]() ,
тобто за означ. Аналогічно визн
,
тобто за означ. Аналогічно визн
![]() .
.
![]() кринолін.
інт. II
роду від ф-ції f(x,y)
по координаті у.
кринолін.
інт. II
роду від ф-ції f(x,y)
по координаті у.
Нех. на кривій АВ
задані функції P(x,y)
і Q(x,y)
![]() -
наз. криволін. інт. II
роду від ф-цій P
і Q
по кривій АВ і познач символом
-
наз. криволін. інт. II
роду від ф-цій P
і Q
по кривій АВ і познач символом
![]()
Обчислення криволінійних інтегралів II роду:
1)крива АВ задана параметрично x=x(t) y=y(t), a≤t≤b, причому ф-ції x(t), y(t) – неперервні разом із своїми похідними x’(t) і y’(t)
![]()
![]()
![]() 2)АВ
задана в явному виді y=y(x),
a≤x≤b
вваж., що ф-ція у=у(х) – неперервне разом
із своєю похідною y’(x).
Тоді крив. інт. II
роду
2)АВ
задана в явному виді y=y(x),
a≤x≤b
вваж., що ф-ція у=у(х) – неперервне разом
із своєю похідною y’(x).
Тоді крив. інт. II
роду
![]()
![]() 3)АВ
задане рівн. х=х(у), с≤у≤d.
Ми
3)АВ
задане рівн. х=х(у), с≤у≤d.
Ми
вважаємо,
що ф-ція х(у) – неперервна разом зі
своєю похідною x’(y), тоді
![]()
![]() Пример
обчислити
Пример
обчислити
![]() ,
АВ: у=х2
парабола,
яка з’єднує тч. А(0,0) і В(1,1)
,
АВ: у=х2
парабола,
яка з’єднує тч. А(0,0) і В(1,1)
За другою ф-лою
![]()
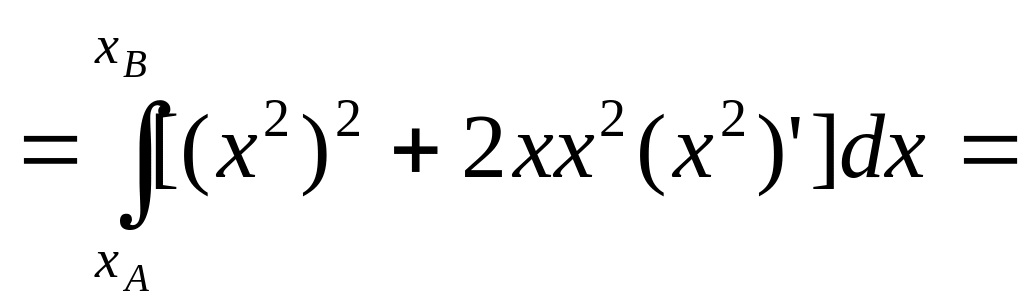
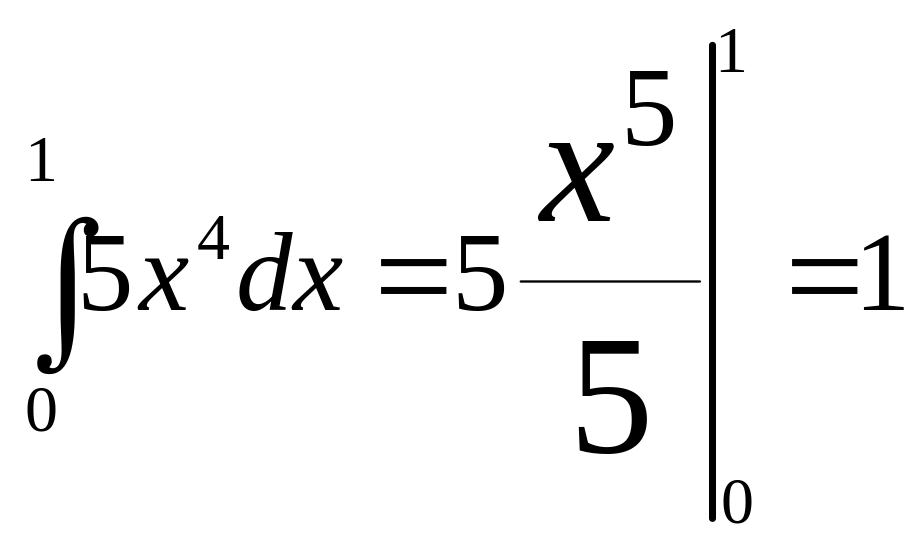
У деяких випадках треба обчислювати крив. інтеграл по замкненому контуру.
В цьому випадку
розглядають дві орієнтації: під додатною
орієнтацією контура розуміють обхід
контура у напрямі, що збігається з
напрямом, який протилежний руху
годинникової стрілки. Тобто це буде
такий обхід обл., при якому внутрішність
обл., яка обмежена кривою АВ залишається
зліва. Крив. інтеграл по замкненому
контуру познач. символом
![]() ;
при обхіді контуру (за годинниковою
стрілкою) вважають від’ємною і познач.
символом
;
при обхіді контуру (за годинниковою
стрілкою) вважають від’ємною і познач.
символом
![]()
Ф-ла Тріна
Теор.: Нех D – деяка правильна обл. у якій задані ф-ції P(x,y) і Q(x,y) і викон. умови:
P(x,y) і Q(x,y) неперервні разом із своїми частинними похідними
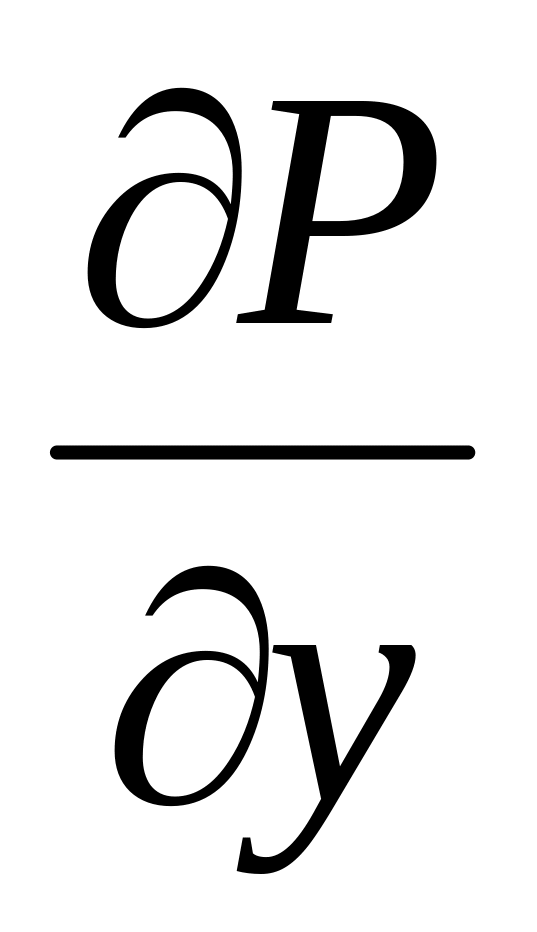 ,
,
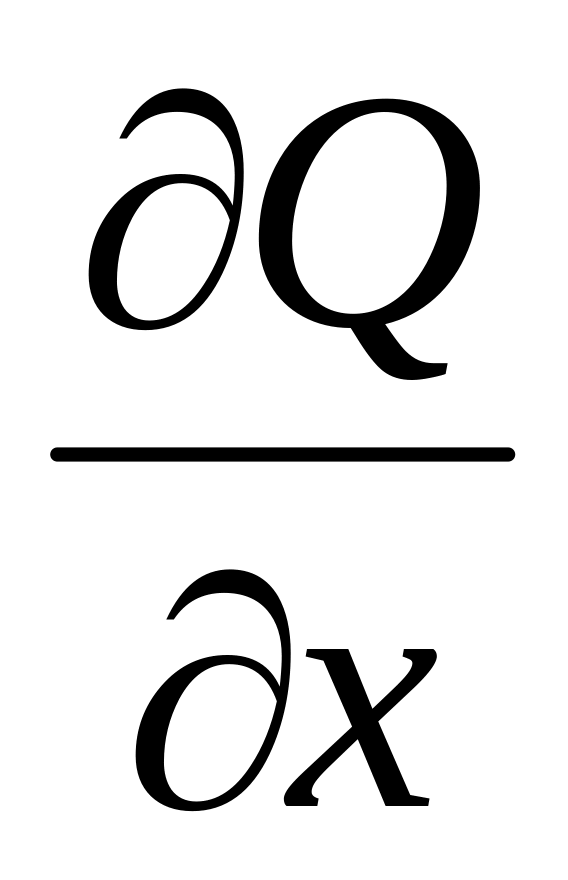 ;
;
2)границя обл. D кусково гладка крива L.
Тоді справдж.
ф-ла Тріна
![]()
![]() (4)
(4)
Ф-ла Тріна (4) зв’язує подвійний інт. і кринолін. інт.
Зауваж.: вияв., що для любих тч. А і В площини хОу кринолін. інт. при обчислені за різними кривими, що з’єднують тч. А і В мають різні знач..
Озн. обл. D у площ. хОу наз. однозв’язною, якщо її межа є одна неперервна замкнена крива без точок само перетину. У випадку, коли межа обл. D з двох замкнених кривих, без точок само перетину обл. D наз. двозв’язною.
Теор.: якщо ф-ції P(x,y) і Q(x,y) неперервні разом із своїми частинними похідними , у деякій однозв’язній обл. DСR2 , то наступні 4 умови еквівалентні:
1) якщо L – довільна неперервна замкнена крива, яка належить обл. D, то криволін. інт.
![]()
2) якщо А і В –
довільні точки обл. D,
то криволін. інт.
![]() не залеж.
від шляху . інт
не залеж.
від шляху . інт
3) існує ф-ція U=U(x,y), визначена в обл. D. Повний дифірінціал якої дорів. dU=Pdx+Qdy
4) у всіх тч. обл. D викон. рівність = .
